高速排序 解析

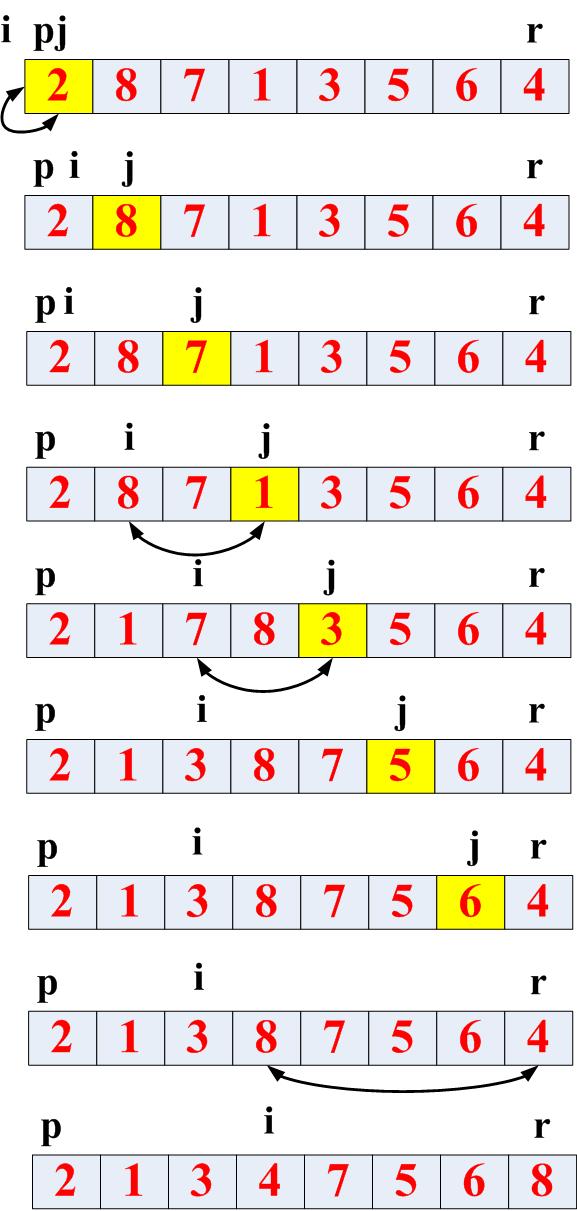
高速排序法原理也是用了分治法，主要原理是将数组分为A[p..q-1] 和A[q+1..r]，然后调整元素使得A[p..q-1]小于等于q，也小于等于A[q+1..r]。然后不断的递归，到最后就排序完毕。

上代码：

// QuickSort.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include<iostream>
using namespace std;

/*函数声明*/
void QuickSort(int *A,int p,int r);	//高速排序
int Partition(int *A,int p,int r);		//分治法
void Display(int *a,int size);			//打印函数

/*主函数*/
int _tmain(int argc, _TCHAR* argv[])
{
	int size,*a;
	while(1)
	{
		cout<<"输入字符串长度："<<endl;
		cin>>size;
		if(size > 0) {
			cout<<"请输入"<<size<<"个待排序数字："<<endl;
			a = (int*)malloc(size*sizeof(int)); //a = new int [size];
			for(int i=0; i<size; i++)  //输入数组
			{
				cin>>a[i];
			}
			QuickSort(a,0,size-1); //调用高速排序函数
		}
		else
			cout<<"输入长度错误！"<<endl;

		Display(a,size);   //打印数组
	}
	return 0;
}

/*函数定义*/
void QuickSort(int *A,int p,int r) //高速排序
{
	int q;
	if(p<r)               //假设p 小于等于 r 那么就程序不运行
	{
		q = Partition(A,p,r);  //调用分治法 找到q的值
		QuickSort(A,p,q-1);
		QuickSort(A,q+1,r);
	}
}

int Partition(int *A,int p,int r) //分治法，作用就是将数组分为A[p..q-1] 和A[q+1..r]
{													//然后调整元素使得A[p..q-1]小于等于q，也小于等于A[q+1..r]
	int x,i,j,temp;

	x = A[r];  //将最后一个值保存在x中
	i = p-1;   //開始的时候将i 移动到数组的外面
	for( j=p; j<=r-1; j++)
	{
		if(A[j]<=x)
		{
			i +=1;
			temp = A[i]; //exchange
			A[i] = A[j];
			A[j] = temp;
		}
	}

	temp = A[i+1];  //exchange
	A[i+1] = A[r];
	A[r] = temp;

	return i+1;  //返回q值
}

void Display(int *a,int size)  //打印函数
{
	    cout<<"排序结果为："<<endl;
		for(int i=0; i<size; i++)    //打印数组
		{
			cout<<a[i]<<" ";
		}
		cout<<endl<<endl;
}

以下我们測试一组数组： 2 8 7 1 3 5 6 4

当中第一次分治法调用示意图例如以下：