[Machine Learning]学习笔记-Neural Networks

引子

对于一个特征数比较大的非线性分类问题，如果采用先前的回归算法，需要很多相关量和高阶量作为输入，算法的时间复杂度就会很大，还有可能会产生过拟合问题，如下图：

这时就可以选择采用神经网络算法。
神经网络算法最早是人们希望模仿大脑的学习功能而想出来的。

一个神经元，有多个树突(Dendrite)作为信息的输入通道，也有多个轴突（Axon）作为信息的输出通道。一个神经元的输出可以作为另一个神经元的输入。神经元的概念和多分类问题的分类器概念很相近，都是可以接收多个输入，在不同的权值(weights)下产生出多个不同的输出。

模型表示

模型可以写成如下形式:

[egin{bmatrix}x_0 ewline x_1 ewline x_2 ewline end{bmatrix} ightarrowegin{bmatrix} ewline end{bmatrix} ightarrow h_ heta(x) ]

上图可以称为单隐层前馈网络，由输入层(X),输出层和它们之间的隐含层构成。

每个输出层都有一个权重矩阵(weights matrix)和一个偏置单元(bias unit)，用来计算输出。

前向传播

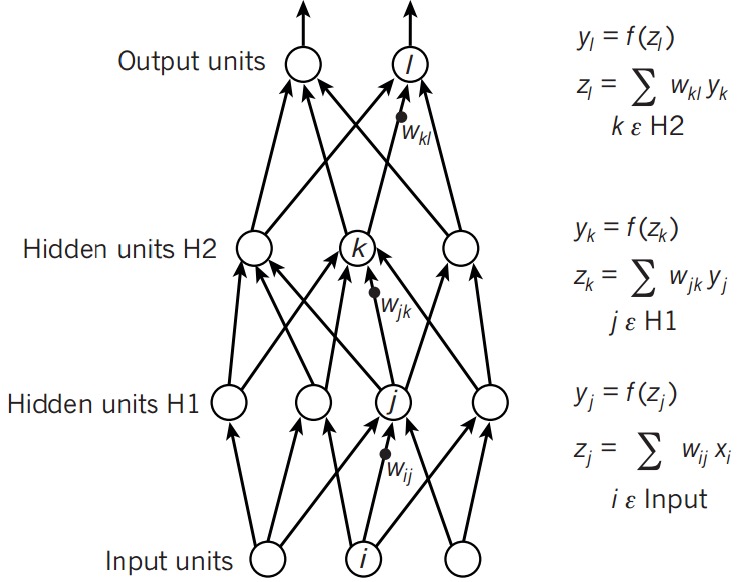
首先回顾一下Logistic Regression的单分类问题中(h_ heta)的计算：

[egin{align*}egin{bmatrix}x_0 ewline x_1 ewline x_2end{bmatrix} ightarrowegin{bmatrix}g(z^{(2)})end{bmatrix} ightarrow h_Theta(x)end{align*} ]

可以写为：

[z^{(2)}=omega^{(2)}a^{(1)}+b^{(2)}\ a^{(2)}=g(z^{(2)})\ h_ heta(x)=a^{(2)} ]

而神经网络的前向传播，也就是在此基础上增加了层数，让一层的输出作为下一层的输入：

[z^{(i)}=omega^{(i)}a^{(i-1)}+b^{(i)}\ a^{(i)}=g(z^{(i)})\ z^{(i+1)}=omega^{(i+1)}a^{(i)}+b^{(i+1)}\ ... ]

需要注意的是，每一层有多个单元，所以这里面的权重也是个二维矩阵。

反向传播（Backpropagation）

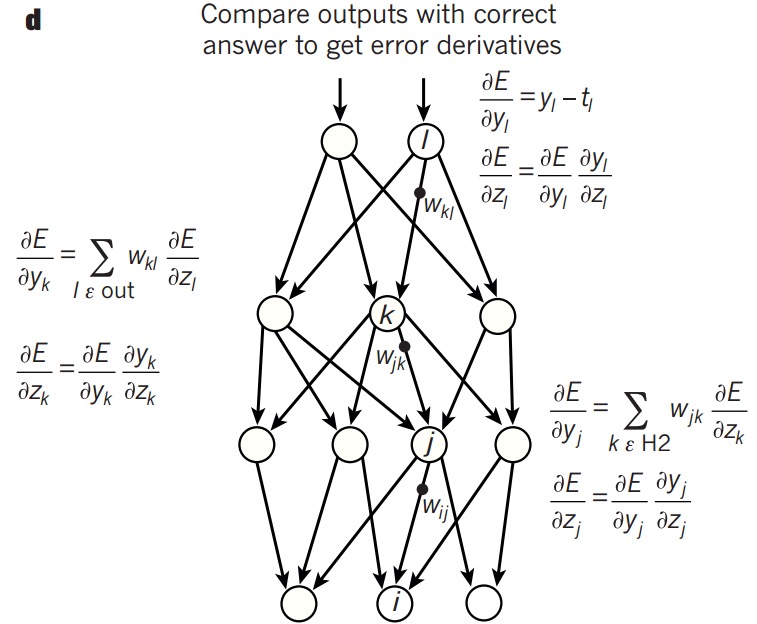
直观理解

但给予初始的偏置单元和权重矩阵后，预测值会不太理想。
那么，如何使预测值符合真实值呢？

[z^{(i)}=omega^{(i)}a^{(i-1)}+b^{(i)} ]

可以发现，可以通过改变每一层的(a,omega,b)来改变最终的输出，但实际上(a)是不能直接改变的。
所以本质上要做的就是改变(omega)和(b)来使预测值接近真实值。
思路和之前的logistic regression和线性回归模型一样，也是先构建代价函数，然后通过梯度下降法使代价方程的值降到最低点，也就得到了合适的(omega)和(b)。
而使用梯度下降法时，需要计算每个(omega)和(b)的梯度，梯度的绝对值越大，说明当前的代价函数对该参数的改变越敏感，改变这个参数使代价函数下降的越快。

微积分公式推导

以3B1B视频中的网络为例：

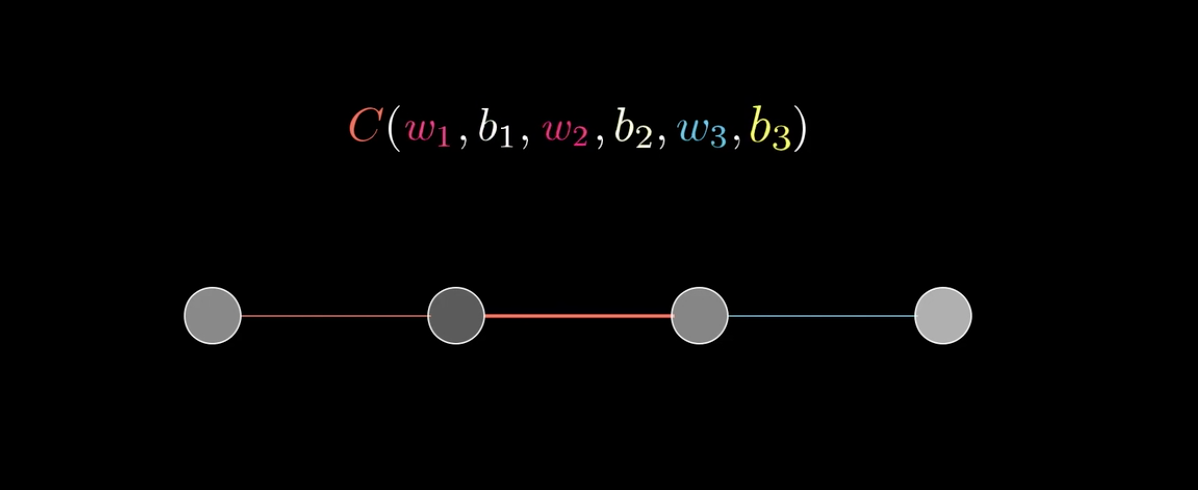
代价方程可以由最后一层的激活值(a^{(L)})和真实值y的均方误差:((a^{(L)}-y)^2)表示。（PS：这里L=4,有些教材计算均方误差时乘上(1/2)）
然后，我们要求解(omega)和(b)的梯度。
在这里以(frac{C_0}{partial omega^{(L)}})为例:

求梯度，也就是求代价函数对参数变化的敏感度。
可以发现，改变(omega^{(L)})，会先影响到(z^{(L)}),然后再影响到(a^{(L)}),最后影响(C_0)。
利用这个特性，可以将(frac{C_0}{partial omega^{(L)}})分解：

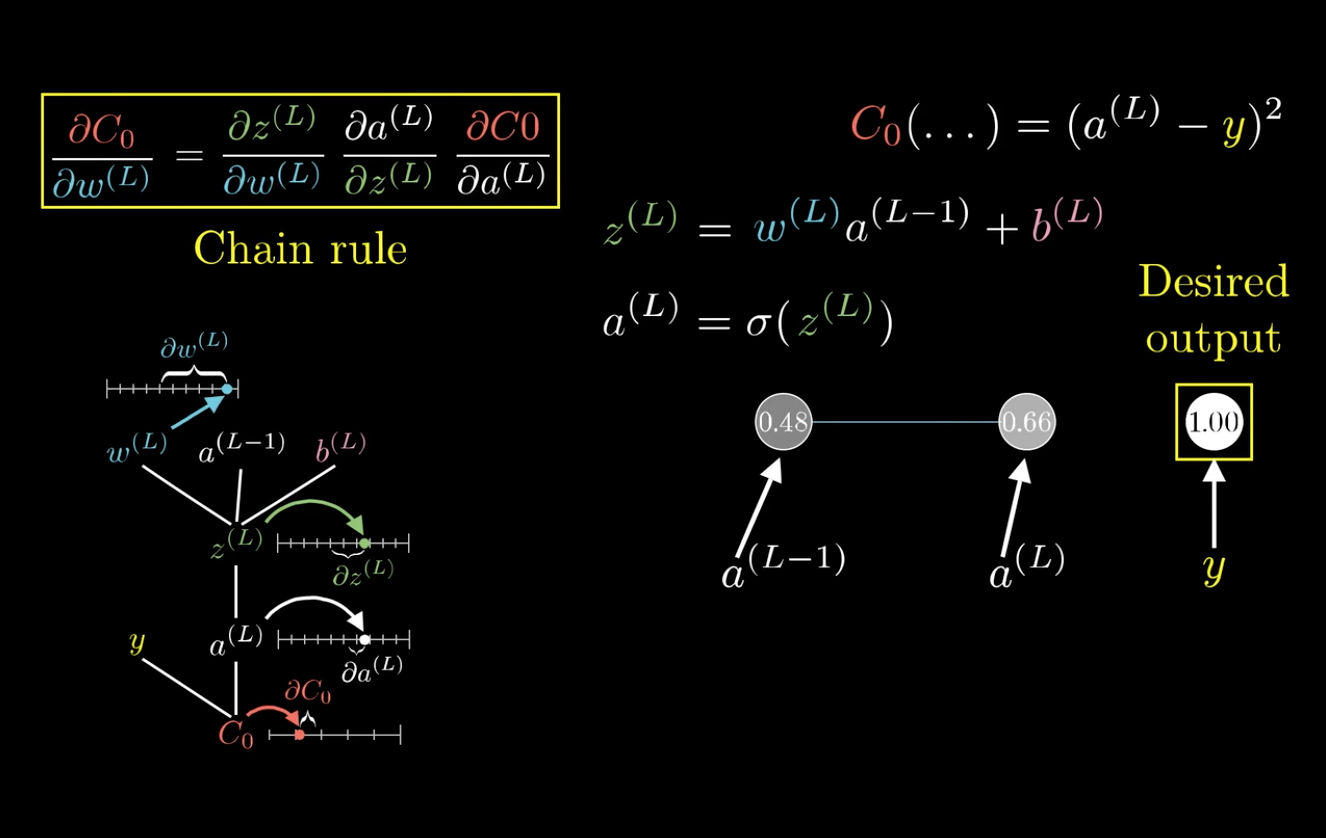
这就是所谓的链式法则(Chain rule):

[egin{split} frac{C_0}{partial omega^{(L)}}=&frac{partial z^{(L)}}{partial omega^{(L)}}frac{partial a^{(L)}}{partial z^{(L)}}frac{partial C_0}{partial a^{(L)}}\ =&a^{L-1}sigmaprime(z^{(L)})2(a^{(L)}-y) end{split}]

同样也可以求得(b^{(L)})的梯度：

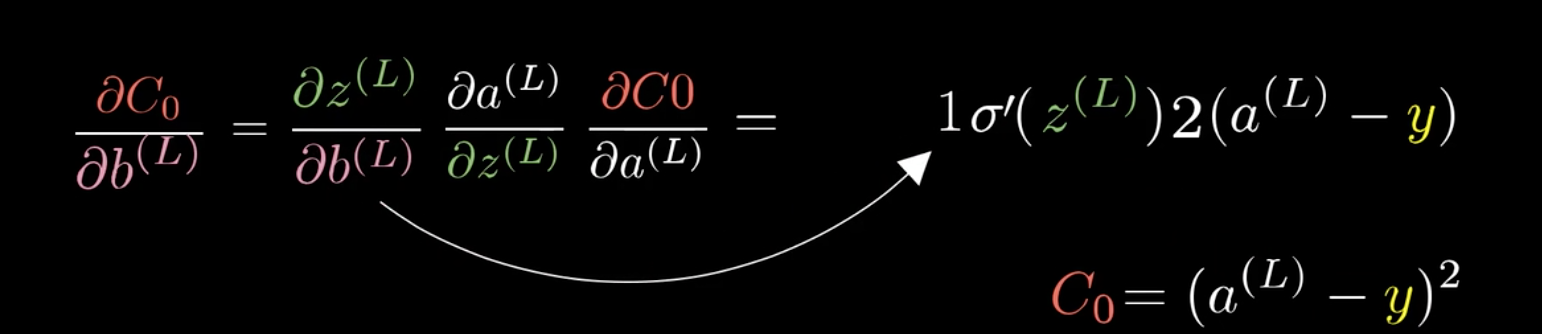
以上的网络每层只有一个神经元，如果有多个单元的话，以上的公式也是成立的。
之前提过，权重矩阵是二维的，可以给两个下标(j,k)表示(omega):

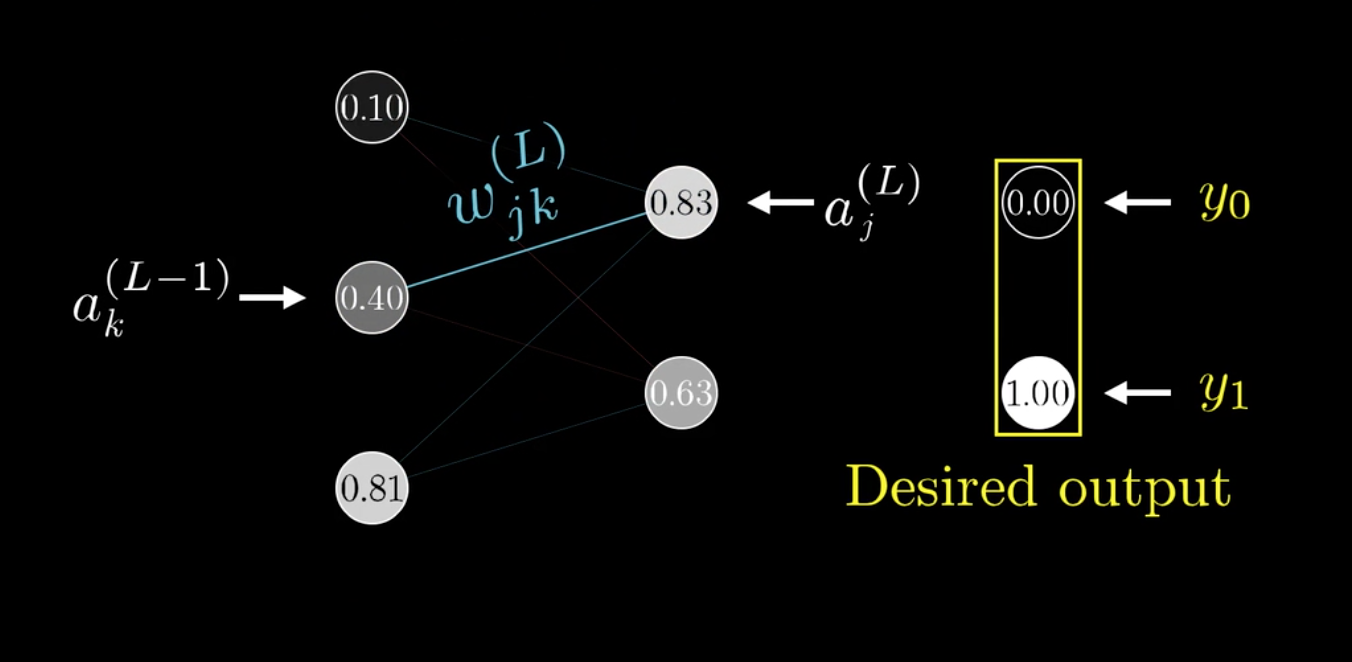
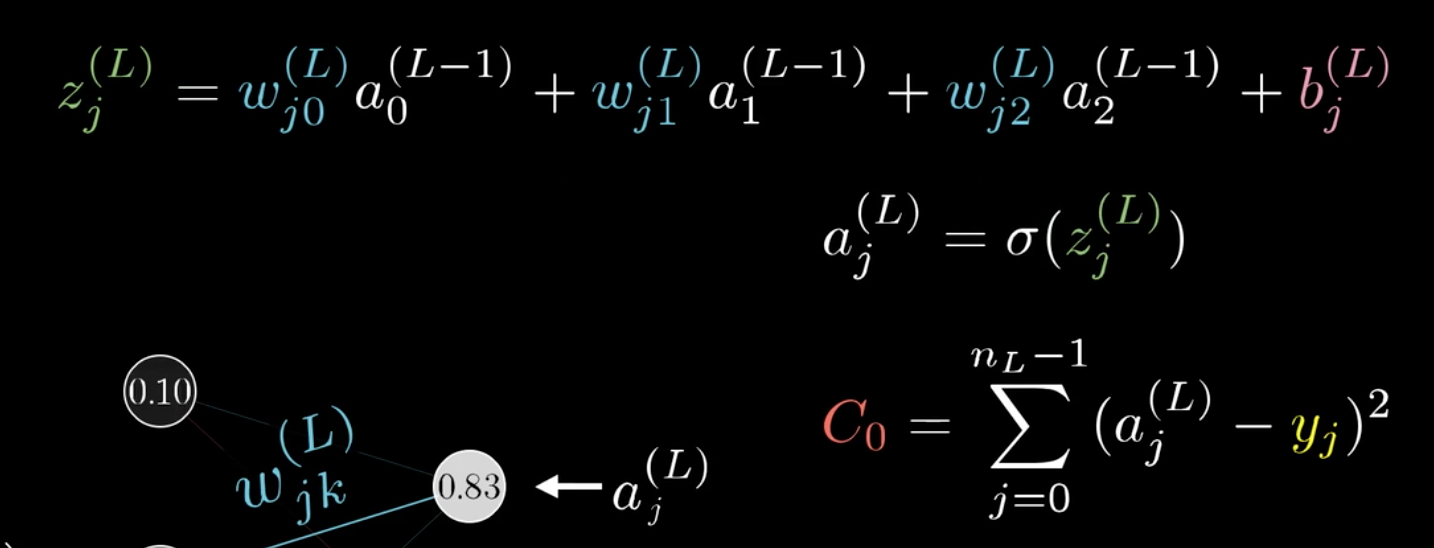
链式法则更新如下：

[egin{split}frac{C_0}{partial omega_{jk}^{(L)}}&= frac{partial z_j^{(L)}}{partial omega_{jk}^{(L)}}frac{partial a_j^{(L)}}{partial z_j^{(L)}}frac{partial C_0}{partial a_j^{(L)}}\ &=a^{L-1}_k sigmaprime(z^{(L)}_j)2(a^{(L)}_j-y_j) end{split}]

而要把这个公式递推到其它层求(frac{C}{partial omega_{jk}^{(l)}})时，只需要变动公式中的(frac{partial C}{partial a_j^{(l)}})即可。
总结如下：

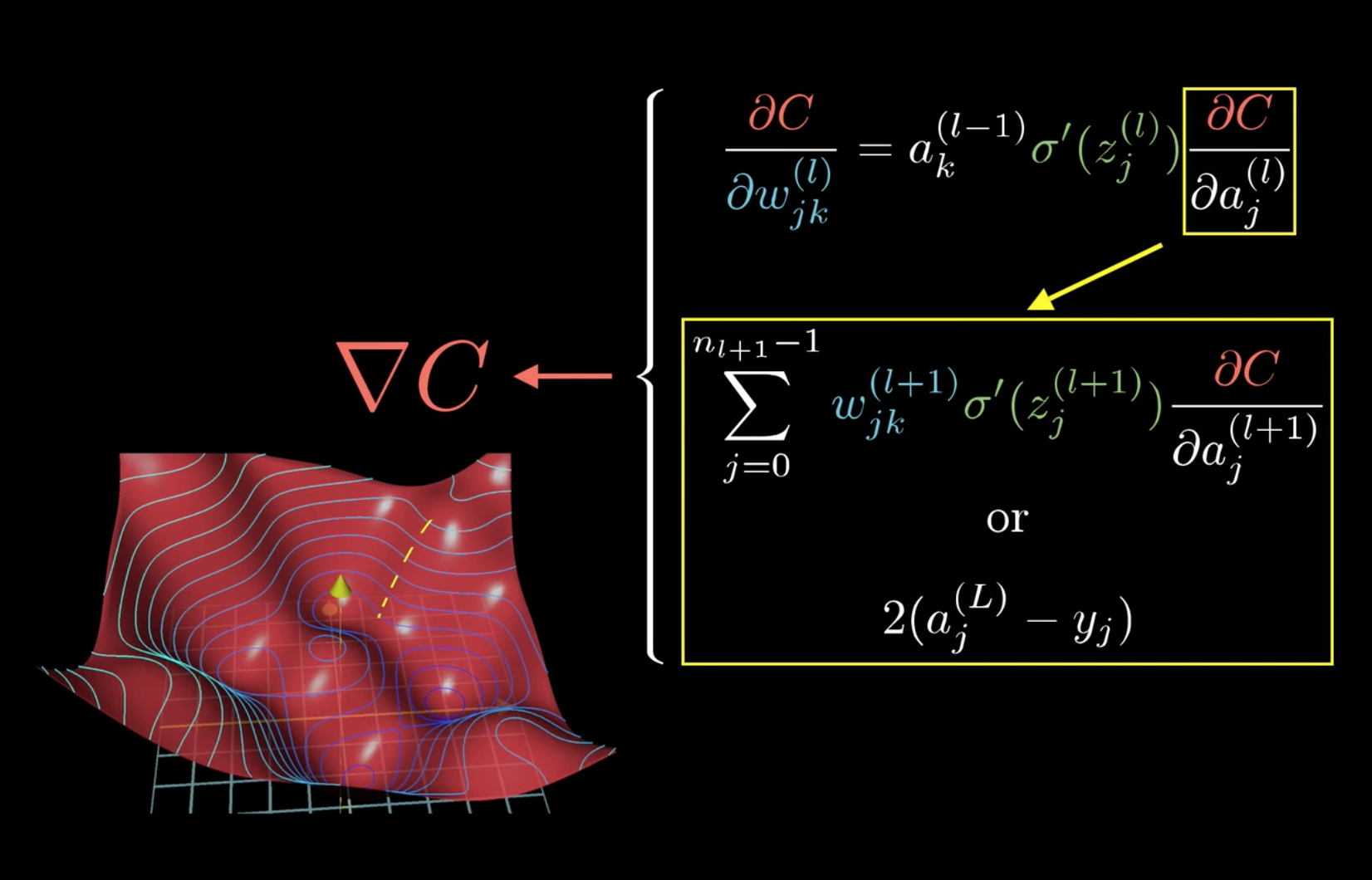
所以，可以发现，计算梯度时，前两项(a^{l-1}_k ,sigmaprime(z^{(l)}_j))是可以直接算出的，而最后一项，则可以先计算出(frac{partial C0}{partial a_j^{(L)}})，然后一层层向前传播即可，反向传播大概也就是这么个意思吧。
Andrew机器学习课程中给出了计算方法，也可以按这个思路去理解了。

TIPS:随机梯度下降法（Stochastic gradient descent）

在之前的batch model中，每次更新权值都要遍历所有的样本然后取均值，这样效率太低，可以把样本分成数个大小相等的mini-batch，每次遍历完一个mini-batch，就更新下权值，虽然下降的路线未必最短，但速度上提升不少，这就是随机梯度下降算法。