转载自:https://www.cnblogs.com/lvchaoshun/p/10645231.html
-
历史
霍夫变换(Hough Transform)是在1959年由气泡室(Bubble Chamber)照片的机器分析而发明,发明者Paul Hough在1962年获得美国专利,被命名为Method and Means for Recognizing Complex Patterns(用于识别复杂图案的方法和手段)。该专利对直线采用斜截距参数化,但由于斜率可能变成无穷大,这有可能导致无限变换空间(unbounded transform space)。
现在使用的霍夫变换是1972年由Richard Duda和Peter Hart所发明,称为“广义霍夫变换[GHT]”(Use of the Hough Transformation to Detect Lines and Curves in Pictures,1972)。
然后1981年在Dana H. Ballard的计算机视觉社区中出现一篇文章名为 Generalizing the Hough transform to detect arbitrary shapes,从而推广开来。
该文描述了使用模板匹配原理对霍夫变换进行修改。要知道霍夫变换最初是为了分析定义的形状(如线、圆、椭圆等)而开发。通过了解其形状并旨在其找出图像中的位置和方向,这种改变使得霍夫变换能够检测用其模型描述的任意对象。这将图像中查找对象(用模型描述)的问题通过查找模型在图像中的位置来解决。利用广义霍夫变换(GHT),找到模型位置的问题转换为寻找将模型映射到图像中的变换参数的问题。给定变换参数的值,就可以确定模型在图像中的位置。
后来产生了更多霍夫变换的变体和扩展,比如KHT,3DKHT,这里不细致说明。霍夫变换经常应用于图像处理中的一种特征提取技术,它通过一种投票算法检测具有特定形状的物体。该过程在一个参数空间中通过计算累计结果的局部最大值得到一个符合该特定形状的集合作为霍夫变换结果。经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆.
-
原理介绍:
1、对于直角坐标系中的任意一点A(x0,y0),经过点A的直线满足Y0=k*X0+b.(k是斜率,b是截距)
2、那么在X-Y平面过点A(x0,y0)的直线簇可以用Y0=k*X0+b表示,但对于垂直于X轴的直线斜率是无穷大的则无法表示。因此将直角坐标系转换到极坐标系就能解决该特殊情况。
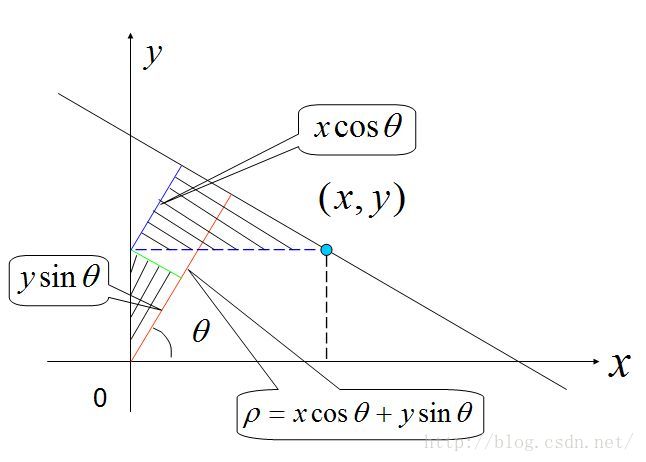
3、在极坐标系中表示直线的方程为ρ=xCosθ+ySinθ(ρ为原点到直线的距离),如图所示:
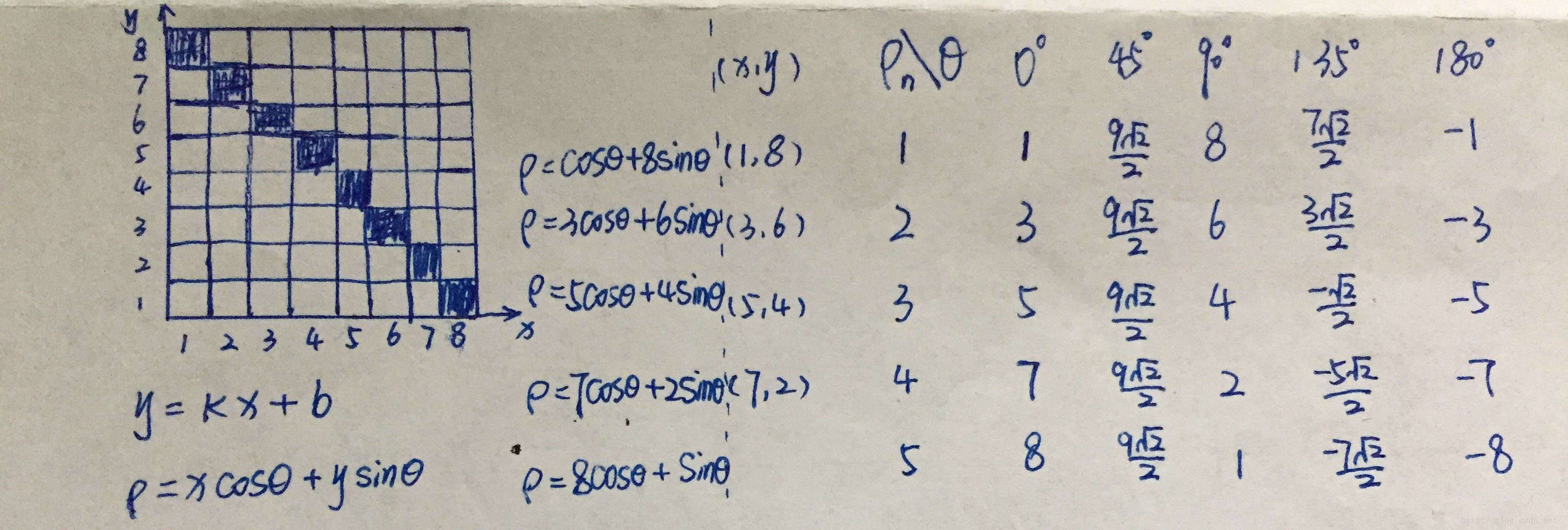
4、如上图,假定在一个88的平面像素中有一条直线,并且从左上角(1,8)像素点开始分别计算θ为0°、45°、90°、135°、180°时的ρ,图中可以看出ρ分别为1、(9√2)/2、8、(7√2)/2、-1,并给这5个值分别记一票,同理计算像素点(3,6)点θ为0°、45°、90°、135°、180°时的ρ,再给计算出来的5个ρ值分别记一票,此时就会发现ρ = (9√2)/2的这个值已经记了两票了,以此类推,遍历完整个88的像素空间的时候ρ = (9√2)/2就记了5票, 别的ρ值的票数均小于5票,所以得到该直线在这个88的像素坐标中的极坐标方程为 (9√2)/2=xCos45°+y*Sin45°,到此该直线方程就求出来了。(PS:但实际中θ的取值不会跨度这么大,一般是1度)。