归并排序的原理
归并排序是利用归并的思想实现的排序方法,该方法采用经典的分治策略(分治法将问题分成一些小的问题然后递归求解,而治的阶段则是将分的阶段得到的答案修补在一起,即分而治之)。
图解归并排序
下面我们以待排序数组 8,4,5,7,1,3,6,2,9,10为例,以图解的方式讲解归并排序的原理。
(1)分治原理图(由于图片太大,没法截全,我进行了一定压缩,所以看起来有点奇怪...)
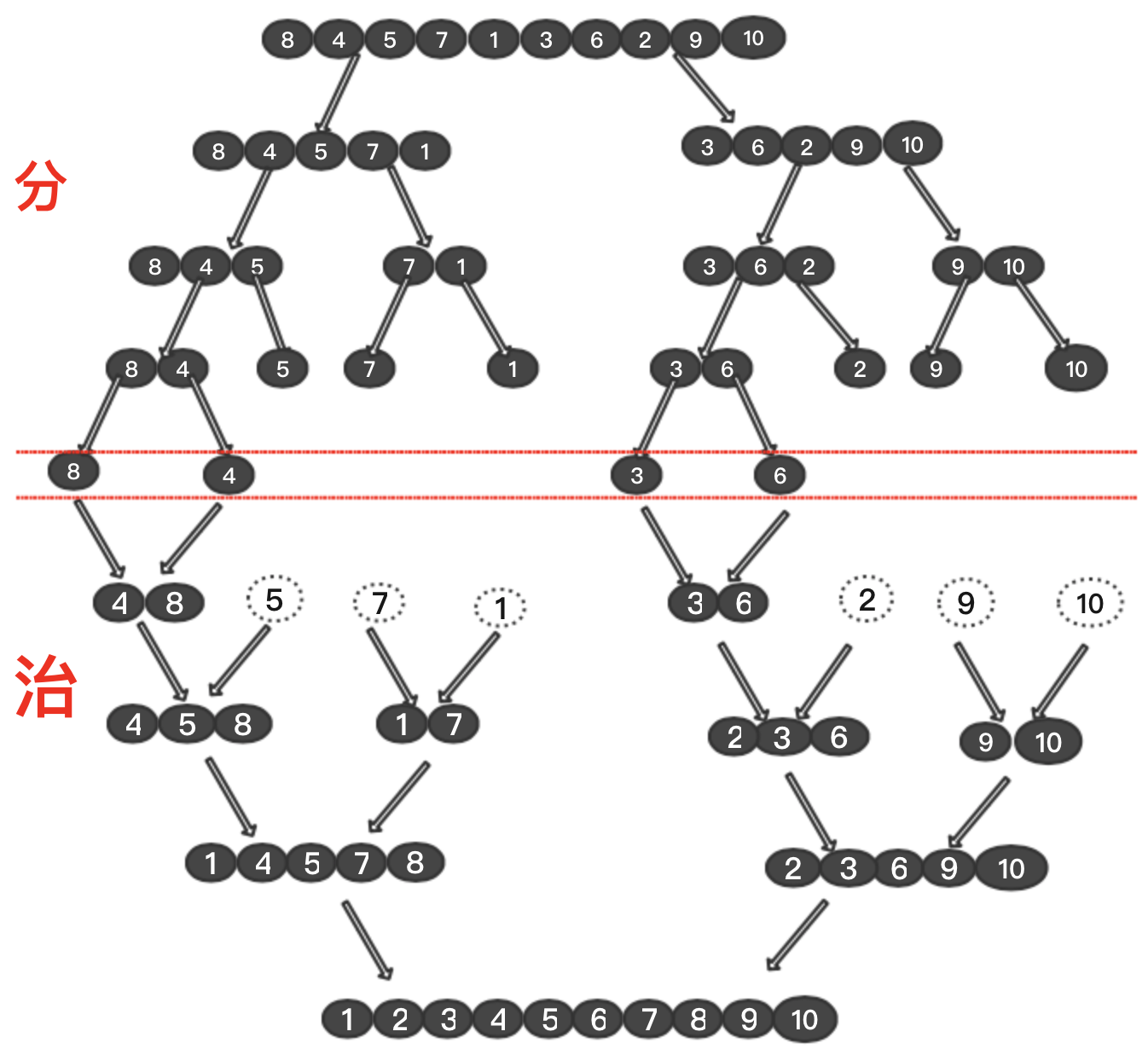
从图中可以看出,归并排序是先将数组进行拆分,拆分到剩余一个关键字,这是一个从大到小的过程。然后再进行治理,治理的过程也就是进行合并的过程,合并时会保证左右两边的数组内部各自有序。然后将两个有序的数组合并到一个数组中,且合并后的数组有序。总结就是:递归拆分,回溯合并,合并时左右两个数组内部有序。
(2)递归原理图
在看递归原理图前,我们先看下归并排序的代码,如下所示
1 public class MergeSort { 2 private static int count = 1; 3 public static void main(String[] args) { 4 int[] arr = {8, 4, 5, 7, 1, 3, 6, 2, 9, 10}; 5 int[] temp = new int[arr.length]; 6 split(arr, 0, arr.length - 1, temp); 7 System.out.println(Arrays.toString(arr)); 8 } 9 10 /** 11 * 递归拆分数组然后合并 12 * 13 * @param arr 待拆分数组 14 * @param left 数组左边下标 15 * @param right 数组右下标 16 * @param temp 用于存放合并后的有序序列的数组 17 */ 18 public static void split(int[] arr, int left, int right, int[] temp) { 19 if (left >= right) { 20 return; 21 } 22 System.out.println("拆分第"+(count++)+"次"); 23 int mid = left + (right - left) / 2; 24 //向左拆分 25 split(arr, left, mid, temp); 26 //向右拆分 27 split(arr, mid + 1, right, temp); 28 //每次拆分后都执行合并 29 merge(arr, left, mid, right, temp); 30 } 31 32 /** 33 * 合并两个各自有序序列(以mid为界) 34 * 35 * @param arr 原始数组 36 * @param left 数组左边下标 37 * @param mid 数组中间下标 38 * @param right 数组右边下标 39 * @param temp 用于存放新的有序数组 40 */ 41 public static void merge(int[] arr, int left, int mid, int right, int[] temp) { 42 int i = left; 43 int j = mid + 1; 44 //temp中的原始下标 45 int t = 0; 46 47 while (i <= mid && j <= right) { 48 //两边数组都没有比较完 继续 49 if (arr[i] < arr[j]) { 50 //左边数组中值更小 51 temp[t] = arr[i]; 52 i++; 53 } else { 54 //右边数组中值更小 55 temp[t] = arr[j]; 56 j++; 57 } 58 t++; 59 } 60 //有一边已经全部复制到temp中了 61 if (i <= mid) { 62 //左边还没有复制完,将左边全部元素复制到temp中 63 while (i <= mid) { 64 temp[t] = arr[i]; 65 i++; 66 t++; 67 } 68 } else if (j <= right) { 69 //右边还没有复制完,将右边全部元素复制到temp中 70 while (j <= right) { 71 temp[t] = arr[j]; 72 j++; 73 t++; 74 } 75 } 76 //将temp复制到原arr中 77 t = 0; 78 while (left <= right) { 79 arr[left] = temp[t]; 80 left++; 81 t++; 82 } 83 } 84 }
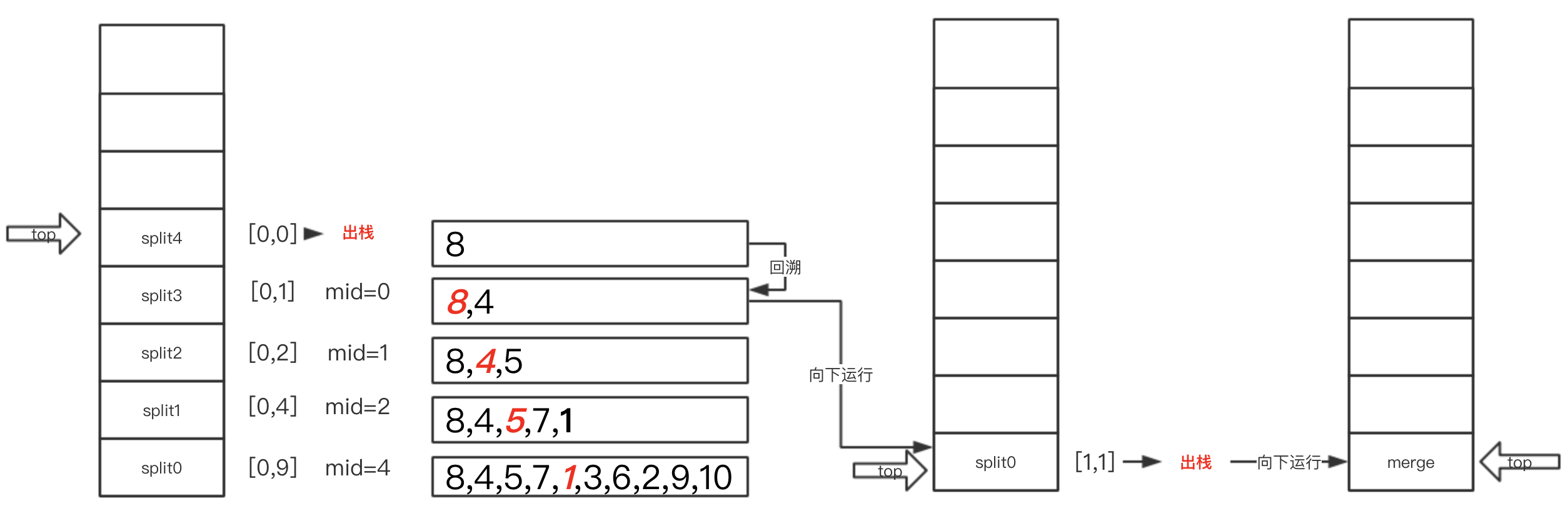
我们都知道在jvm内存模型中,线程每调用一个方法就会将该方法压入本线程的栈中。在递归方法的调用过程中也是如此,只不过每次压栈的方法名都相同,这里我们为了好区分递归执行到哪一层,人为的为递归方法编号,即每递归一次编号加1。如上图所示,数组8,4,5,7,1,3,6,2,9,10第一次拆分时,left = 0,right=9,mid=4 (三者均表示下标),然后继续向左递归拆分即split1方法入栈,此时left=0,right=4,mid=2。然后继续向左递归拆分。。。。直到left=right即只剩下一个数字无法再拆分,即我们上图中的split4,所以split4方法出栈回溯到方法split3中,split3代码向下执行,执行向右递归拆分,这里我们为了方便区分,将向右递归的过程又画了一个栈来表示,即上图中间的栈图,此时向右递归的split0入栈,此时left=right=1,split0出栈,split3继续向下执行,即执行merge合并方法,此时合并方法参数left=0,right=1,mid=0,即8和4两个分别有序的数组进行合并(单个数字内部当然有序)。
merge方法执行完后,split3递归方法执行完毕,出栈,回溯到递归方法split2中,继续执行上述步骤。需要说明的是,上述过程在向右递归时由于mid后面只有一个数字4,所以left=right=1,所以向右递归方法直接出栈,而在向左递归执行到split1时,mid后面有两个数字7,1所以在向右递归时会将当前数组(7,1)继续执行向左向右拆分,以保证数组与其他数组进行合并前内部有序。
(3)合并图解
下面以最后一次合并为例,图解合并的执行过程。即1,4,5,7,8与2,3,6,9,10两个有序数组的合并过程










(4)总结
以上就是归并排序的执行原理,主要分为以下步骤:
1.递归的方式进行拆分,将大的数组拆分成小的数组,直到剩余一个不能拆分
2.回溯的时候进行合并,合并时以mid为界,左右两边各自有序,通过额外的空间temp数组,将两个有序数组合并到一个有序数组中
3.将合并后的数组复制到原数组中,当回溯完成时整个数组有序