根据先序遍历中序遍历重建二叉树

根据先序遍历和中序遍历的特点，我们想到了采用递归的方法来实现。

思路：1） 代码的容错性检查，比如：先序遍历和中序遍历长度应相等

        2） 先保存先序遍历的第一个点，这个点为结点，接下来循环中序遍历，直到midOrd[index]=该结点，那么接下来就可以采用递归，分别对结点左边和右边的序列采用相同的方法。

        3） 直到中序遍历中的序列中只含一个点，整个过程结束。

下面是我写的代码，一直显示错误，不知道什么原因。

// 先序中序重建二叉树.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <iostream>
using namespace std;

typedef int type;
typedef struct bitNode
{
    type data;
    bitNode *leftTree;
    bitNode *rightTree;
    
}bitTree,*BitTree;

void rebuildTree(bitTree**T,type pre_order[],int pre_left,int pre_right,type mid_order[],int mid_left,int mid_right)
{
    int index;
    int length;                 //每个序列的长度
    //1.容错性判断
    if((pre_right-pre_left)!=(mid_right-mid_left))
    {
        cout<<"错误1!"<<endl;
        return ;
    }
    //2.每次新建一个节点，将先序遍历序列的第一个元素保存下来
    (*T)=new bitTree;
    (*T)->data=pre_order[pre_left];
    (*T)->leftTree=NULL;
    (*T)->rightTree=NULL;
    
    
    //3.遍历中序序列，如果找到与上一节点元素相同，则退出循环。此时就可以对其构建二叉树
    for (index=mid_left;index<=mid_right;index++)
    {
        if (mid_order[index]==(*T)->data)
            break;
    }
    
    if ((index-1)>mid_right)
    {
        cout<<"错误2!"<<endl;
        return ;
    }
    
    
    //4.递归调用，分别对中序序列的左右两边进行递归。注意递归条件。如果只有一个元素就不递归。
    //中序遍历序列中的左边序列
    if((index-mid_left)>0)    //必须保证中序遍历序列中左边或者右边有元素的时候才会去递归调用
    {
        length=index-pre_left;
        rebuildTree(&((*T)->leftTree),pre_order,pre_left+1,pre_left+1+length-1,mid_order,mid_left,mid_left+length-1);
    }    
    //中序遍历序列中右边的序列
    if ((mid_right-index)>0)
    { 
        length=mid_right-index;
        rebuildTree(&((*T)->rightTree),pre_order,index+1,index+1+length-1,mid_order,index+1,index+1+length-1);   
    }
    
}

void postVisit(bitTree *tree)
{
    if (tree)
    {
        postVisit(tree->leftTree);
        postVisit(tree->rightTree);
        cout<<tree->data<<endl;
    }
    
}


int main(int argc, char* argv[])
{
    type preOrder[]={1,2,4,5,3,6};
    type midOrder[]={4,2,5,1,6,3};
    bitTree *Tree;
    rebuildTree(&Tree,preOrder,0,5,midOrder,0,5);
    postVisit(Tree);
    return 0;
}

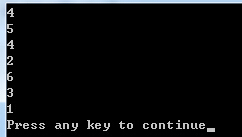
可以得到答案的程序：

// 先序中序重建二叉树.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include <iostream>
using namespace std;

typedef int type;
typedef struct bitNode
{
   type data;
   bitNode *leftTree;
   bitNode *rightTree;

}bitTree,*BitTree;

BitTree rebuildTree(type pre_order[],int pre_left,int pre_right,type mid_order[],int mid_left,int mid_right)
{
    int index;
    int length;                 //每个序列的长度
    //1.容错性判断
    if((pre_right-pre_left)!=(mid_right-mid_left)||(pre_left>pre_right))
        return NULL;

    //2.每次新建一个节点，将先序遍历序列的第一个元素保存下来

   BitTree T=new bitTree;
   T->data=pre_order[pre_left];
   T->leftTree=NULL;
   T->rightTree=NULL;


//3.遍历中序序列，如果找到与上一节点元素相同，则退出循环。此时就可以对其构建二叉树
    for (index=mid_left;index<=mid_right;index++)
    {
        if (mid_order[index]==T->data)
            break;
    }

    if (index>mid_right)
       return NULL;
   
 
    //4.递归调用，分别对中序序列的左右两边进行递归。注意递归条件。如果只有一个元素就不递归。
    //中序遍历序列中的左边序列
    if((index-mid_left)>0)    //必须保证中序遍历序列中左边或者右边有元素的时候才会去递归调用
    {
        length=index-pre_left;
        T->leftTree= rebuildTree(pre_order,pre_left+1,pre_left+1+length-1,mid_order,mid_left,mid_left+length-1);
    }    
    //中序遍历序列中右边的序列
    if ((mid_right-index)>0)
    { 
        length=mid_right-index;
        T->rightTree= rebuildTree(pre_order,pre_right-length+1,pre_right,mid_order,mid_right-length+1,mid_right);   
    }
    return T;              //要返回头结点，所以注意别掉了。
       
}

void postVisit(bitTree *tree)
{
    if (tree)
    {
        postVisit(tree->leftTree);
        postVisit(tree->rightTree);
        cout<<tree->data<<"  ";
    }
    
}


int main(int argc, char* argv[])
{
    type preOrder[]={1,2,4,5,3,6};
    type midOrder[]={4,2,5,1,6,3};
    BitTree Tree;
    Tree=rebuildTree(preOrder,0,5,midOrder,0,5);
    postVisit(Tree);
    return 0;
}