BST存在的问题:
BST存在的主要问题是,数在插入的时候会导致树倾斜,不同的插入顺序会导致树的高度不一样,而树的高度直接的影响了树的查找效率。
理想的高度是logN,最坏的情况是所有的节点都在一条斜线上,这样的树的高度为N。
平衡二叉查找树:
平衡树在插入和删除的时候,会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别为AVL树和红黑树。
AVL树由于实现比较复杂,而且插入和删除性能差,在实际环境下的应用不如红黑树。
红黑树:
红黑树是一个平衡的二叉树,但不是一个完美的平衡二叉树。
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
在C++ STL中,很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化,这些修改提供了更好的性能,以及对set操作的支持)
Java 8中HashMap和ConcurrentHashMap都有用到红黑树。
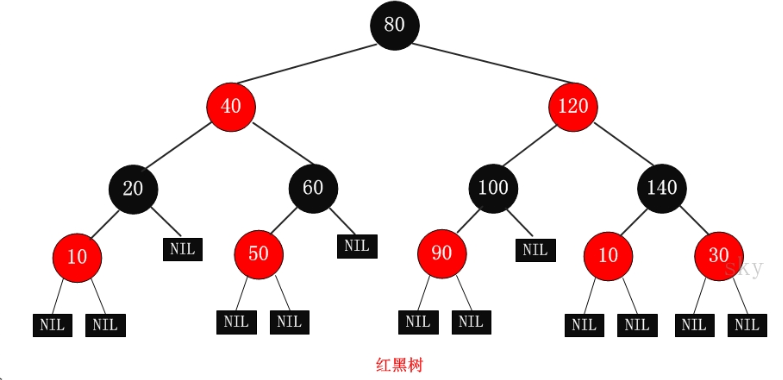
红黑树的特性:
每个节点是红色或者黑色。
根节点是黑色。
每个叶子节点(NIL)是黑色。(这里叶子节点,是指为空(NIL或NULL)的叶子节点!)
如果一个节点是红色的,则它的子节点必须是黑色的。(也就是说不存在两个连续的红色节点)
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这些特性约束了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。
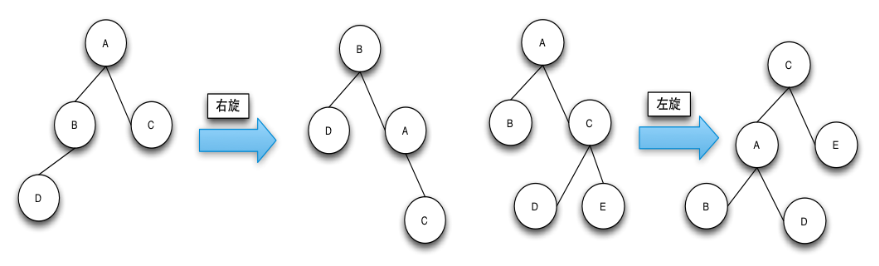
旋转:
旋转操作(Rotate)的目的是使节点颜色符合定义,让红黑树的高度达到平衡。
总结:
作为平衡二叉查找树里面众多的实现之一,红黑树无疑是最简洁、实现最为简单的。
红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。
作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色。
红黑树里面的插入和删除的操作比较难理解,这时要注意记住一点:操作之前红黑树是平衡的,颜色是符合定义的。在操作的时候就需要向兄弟节点、父节点、侄子节点借调和互换颜色,要达到这个目的,就需要不断的进行旋转。
所以红黑树的插入删除操作需要不停的旋转,一旦借调了别的节点,删除和插入的节点就会达到局部的平衡(局部符合红黑树的定义),但是被借调的节点就不会平衡了,这时就需要以被借调的节点为起点继续进行调整,直到整棵树都是平衡的。在整个修复的过程中,插入具体的分为3种情况,删除分为4种情况。
整个红黑树的查找,插入和删除都是O(logN)的,原因就是整个红黑树的高度是logN,查找从根到叶,走过的路径是树的高度,删除和插入操作是从叶到根的,所以经过的路径都是logN。