题目描述
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例 1 :
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :
数组的长度为 [1, 20,000]。
数组中元素的范围是 [-1000, 1000] ,且整数 k 的范围是 [-1e7, 1e7]。
思路
看到这题,我唯一能想到的解决方法就是暴力法(或枚举法)。
定下两个下表start、end,使用两次for循环,外层关于end并依次从0开始向后移动,内层关于start并从end开始向前移动。
因为题目中要求的是“连续的子数组”,因此就直接构造了[start,end]的数组,并对其求和sum。
只要sum值等于k值,那我们用计数count记录。
最后函数返回count即可。
方法很简单,这样分析的话,不需要用到什么额外的空间,所以空间复杂度为O(1);时间复杂度方面,由于使用两次for循环对数组进行遍历为O(n^2),再加上求和时间为O(1),因此总体的时间复杂度为O(n^2)。
代码
class Solution {
//注意题中说的是“连续的子数组”
public int subarraySum(int[] nums, int k) {
int count = 0;
// 计算[start,end]构成的子数组的和sum
for(int end = 0; end < nums.length; end++) {
int sum = 0;
for (int start = end; start >= 0; start--) {
sum += nums[start];
if(sum == k)
count++;
}
}
return count;
}
/*
时间复杂度:O(n^2),n为数组的长度;两层循环O(n^2)+求和时间为O(1)
空间复杂度:O(1),无需其他存储空间的使用
*/
}
执行

题后心得
刚看到这题的时候,注意到难度为“中等”,我想肯定不止有这种方法,而且这种方法过于简单,肯定有更高效的、更有技术含量的算法。
于是,去看了他人的算法,发现使用了哈希表。
可是,我还不会哈希表啊
接下来这段时间,得找时间把哈希表这块学一点。
接下来的话特别有意思、深刻:
提交后,我也顺便看了一下评论,有意思的是,我发现了“老马”。
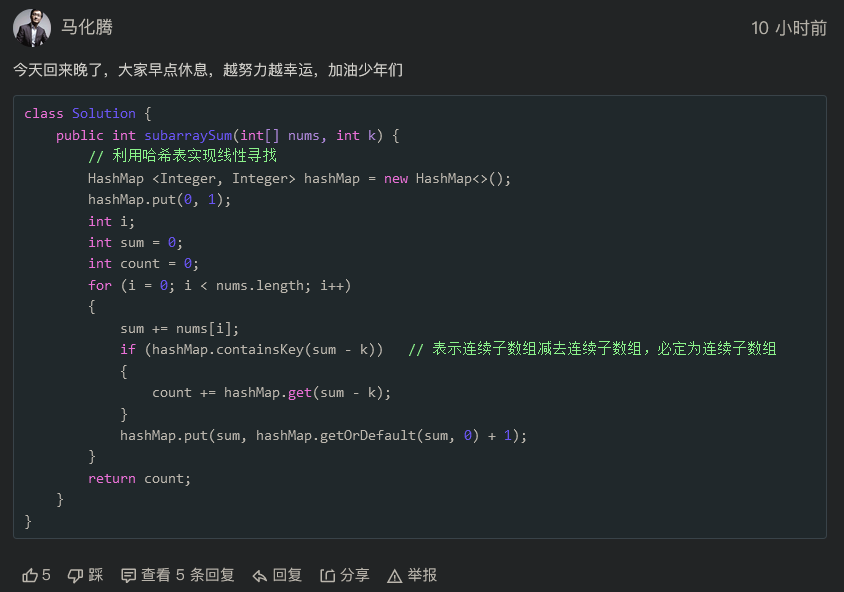
当然,是假的!!!