题意:给出一个序列,随机取出其中一条最长上升子序列,问你取到每个数的概率是多少。
说起概率,我们可以尝试去求最长上升子序列的个数,显然每个点被取到的概率是 含有这个点的最长上升子序列个数/总共最长上升子序列的个数。
首先我们假设dp[i]为到这个点的最长上升子序列长度。
这个事情我们需要建立一个分层图,第x层含有dp[i]=x的点。
举个例子,对于序列A 1 7 6 8 2 4 3
它的dp数组值是 1 2 2 3 2 3 3
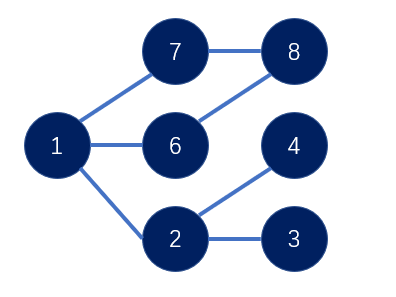
我们就可以建立一个这样的图,来求从前往后取最长上升子序列的方案数,比如8的方案就可以从7、6继承。
点1的方案数显然是1,6和7则从1继承来了这个方案数,所以也是1,8则从7、6继承,于是方案数是2。
当然我们不能直接建边,那样复杂度就不能接受了,我们得利用线段树来求一个点前驱方案数之和。
好了,到了这里,我们求出了从前往后到这个点的方案数的和,但是这显然不是最终答案,比如例子中的2,顺着的方案数显然是1,但是却有1-2-4和1-2-3两种方案!
怎么办呢?很简单,我们只要反着从后往前再求一次这个方案数,将正反方案数相乘,就是包含这个点的方案数总和,例如点2就是1*2=2,这样就符合答案了。
代码:
#include<bits/stdc++.h>
using namespace std;
const long long mod=998244353;
int i,i0,n,m,a[500005],tree[4*500005],dp[500005],d[500005],dd[500005];
long long ans[500005];
vector<int>v,q[500005];
void extgcd(long long a,long long b,long long& d,long long& x,long long& y)
{
if(!b){d=a;x=1;y=0;}
else{extgcd(b,a%b,d,y,x);y-=x*(a/b);}
}
long long inv(long long a,long long n)
{
long long d,x,y;
extgcd(a,n,d,x,y);
return d==1?(x+n)%n:-1;
}
void c_tree(int l,int r,int p,int a,int v)
{
if(l==r)tree[p]=v;
else
{
int mid=(l+r)/2;
if(a<=mid)c_tree(l,mid,p*2,a,v);
else c_tree(mid+1,r,p*2+1,a,v);
tree[p]=max(tree[p*2],tree[p*2+1]);
}
}
int q_tree(int l,int r,int p,int a,int b)
{
if(a==l&&b==r)return tree[p];
int mid=(l+r)/2;
if(b<=mid) return q_tree(l,mid,p*2,a,b);
else if(a>=mid+1)return q_tree(mid+1,r,p*2+1,a,b);
else return max(q_tree(l,mid,p*2,a,mid),q_tree(mid+1,r,p*2+1,mid+1,b));
}
void c0_tree(int l,int r,int p,int a,int v)
{
if(l==r)
{
tree[p]+=v,tree[p]%=mod;
if(tree[p]<0)tree[p]+=mod;
}
else
{
int mid=(l+r)/2;
if(a<=mid)c0_tree(l,mid,p*2,a,v);
else c0_tree(mid+1,r,p*2+1,a,v);
tree[p]=(tree[p*2]+tree[p*2+1])%mod;
}
}
int q0_tree(int l,int r,int p,int a,int b)
{
if(a==l&&b==r)return tree[p];
int mid=(l+r)/2;
if(b<=mid) return q0_tree(l,mid,p*2,a,b);
else if(a>=mid+1)return q0_tree(mid+1,r,p*2+1,a,b);
else return (q0_tree(l,mid,p*2,a,mid)+q0_tree(mid+1,r,p*2+1,mid+1,b))%mod;
}
int main()
{
scanf("%d",&n);
for(i=1;i<=n;i++)scanf("%d",&a[i]),v.push_back(a[i]);
sort(v.begin(),v.end()),v.erase(unique(v.begin(),v.end()),v.end());
for(i=1;i<=n;i++)a[i]=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1;
int mx=0;
for(i=1;i<=n;i++)
{
dp[i]=q_tree(0,n,1,0,a[i]-1)+1;
q[dp[i]].push_back(i),mx=max(mx,dp[i]);
c_tree(0,n,1,a[i],dp[i]);
}
memset(tree,0,sizeof(tree));
for(int i0:q[mx])
{
dd[i0]=1;
}
memset(tree,0,sizeof(tree));
for(i=mx;i>=2;i--)
{
for(int x=q[i-1].size()-1,y=q[i].size()-1;x>=0;x--)
{
while(y>=0&&q[i][y]>q[i-1][x])c0_tree(0,n+1,1,a[q[i][y]],dd[q[i][y]]),y--;
dd[q[i-1][x]]=q0_tree(0,n+1,1,a[q[i-1][x]]+1,n+1);
}
for(int x=q[i-1].size()-1,y=q[i].size()-1;x>=0;x--)
{
while(y>=0&&q[i][y]>q[i-1][x])c0_tree(0,n+1,1,a[q[i][y]],-dd[q[i][y]]),y--;
}
}
for(int i0:q[1])
{
d[i0]=1;
}
for(i=2;i<=mx;i++)
{
for(int x=0,y=0;x<q[i].size();x++)
{
while(y<q[i-1].size()&&q[i-1][y]<q[i][x])c0_tree(0,n+1,1,a[q[i-1][y]],d[q[i-1][y]]),y++;
d[q[i][x]]=q0_tree(0,n+1,1,0,a[q[i][x]]-1);
}
for(int x=0,y=0;x<q[i].size();x++)
{
while(y<q[i-1].size()&&q[i-1][y]<q[i][x])c0_tree(0,n+1,1,a[q[i-1][y]],-d[q[i-1][y]]),y++;
}
}
for(i=1;i<=mx;i++)
{
long long sum=0;
for(int x:q[i])sum+=(long long)d[x]*dd[x],sum%=mod;
for(int x:q[i])ans[x]=(long long)d[x]*dd[x]%mod*inv(sum,mod)%mod;
}
for(i=1;i<=n;i++)printf("%lld%c",ans[i],i==n?'
':' ');
return 0;
}