参考链接: https://www.zhihu.com/question/54504471/answer/611222866
- 参考链接: http://bbs.cvmart.net/articles/281/cong-cnn-dao-gcn-de-lian-xi-yu-qu-bie-gcn-cong-ru-men-dao-jing-fang-tong-qi
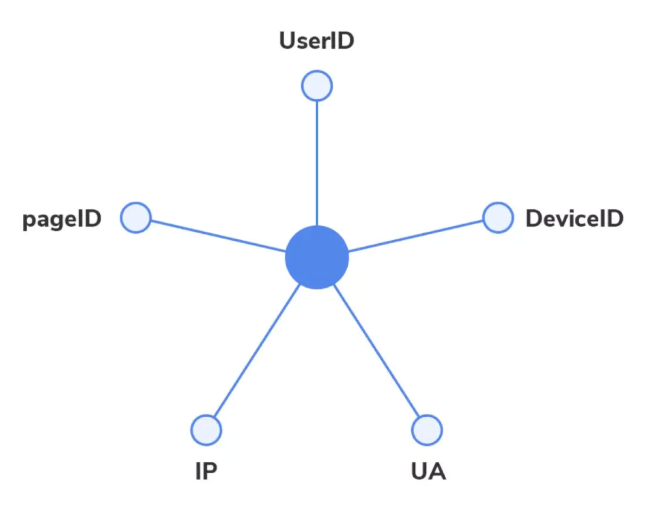
- L = D - A, A 为图的邻接矩阵, D 为顶点度的对角矩阵, L 为 拉普拉斯矩阵
1.1 拉普拉斯矩阵的类别


3 图卷积的参数
- 参考链接: http://bbs.cvmart.net/articles/281/cong-cnn-dao-gcn-de-lian-xi-yu-qu-bie-gcn-cong-ru-men-dao-jing-fang-tong-qi
- 由 1 小节得知, 图卷积的公式, 图卷积训练的参数在公式中对角矩阵中, GCN 的训练有两个版本, 第一版思维简单但是因为其缺点已经不再使用, 现在大都使用第二个版本
3.1 第一代图卷积训练
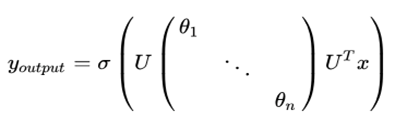
- 直接将对角矩阵中对角上的值当做参数
- 表示激活函数
- 表示输入向量
- 优点
- 发现中间的除去 的公式为拉普拉斯矩阵的分解公式, 那么在运算中不再需要分解公式, 直接使用拉普拉斯矩阵即可, 减少了计算量
- 参数少
3.2 第二代图卷积训练

- 将 转为了 , 其中为任意参数, 需要进行随机初始化, 即边的权重
- 借助 U 和拉普拉斯矩阵的特征进行化简, 得到
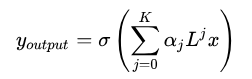
- L 表示拉普拉斯矩阵
- K 表示顶点的阶数, 顶点的邻居节点
- x 表示输入的特征, 为了形象的理解, 以一张灰度图为例
- 图的结构即图像的方格排列, 不需要人为的设计, 因为图片的形状就是如此, 每一个方格是图的一个顶点
- 像素值即每一个顶点的特征, 只不过在一般的图结构中, 顶点的值为一个特征向量
- 表示边的权重, 也是网络需要训练并且优化的参数
3.3 图解图卷积
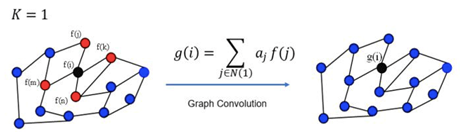

- GCN每一次卷积对所有的顶点都完成了图示的操作
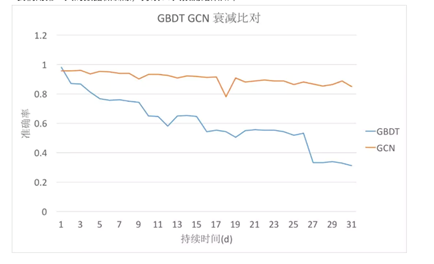
4 GCN 分类的效果
5 图卷积网络的拓扑结构
- 参考链接: https://mp.weixin.qq.com/s/356WvVn1Tz0axsKd8LJW4Q
- 拓扑结构
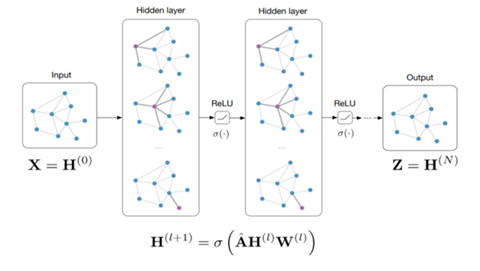
- 和 CNN 类似, 每一层都是叠加堆积在一起的, 经过卷积得到的结果, 通过激活函数(ReLU, Sigmoid等)传到下一层
- 不是每一个顶点都要进行卷积重新计算新的特征, 而是选择靠近中心的顶点
- 在上图中, 表示的不是图的结构, 也不是边所代表的的权重, 而是每一个顶点对应的特征向量, 在图片中, 每一个顶点对应的是一个标量, 即像素值
- 在3 图卷积的参数中提到了图卷积的参数与公式, 第二代的图卷积公式在运用的时候回转变成一个更清晰的表示公式
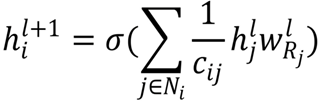
- 表示标准化系数
- H 表示上一层每一个顶点的特征向量, 维度为 NxF, N 表示顶点个数, F 表示特征向量的维度
- W 表示边权重
- 公式的定性理解
- 选定一个顶点 V, 确定邻域, 如果个数不到邻域个数, 则补充哑顶点, 如果超过, 则删除对于的顶点
- 获取邻域中顶点的特征向量, 将其余顶点 V 的边(权重)相乘再相加, 得到新的维度的特征向量
- 防止较大的尺度变化, 将得到的结果进行标准化
- 图卷积的特点