红黑树的删除

1.前文回顾

　　上一篇随笔写到了红黑树的实现及其各种功能的实现，本文将讲红黑树的删除。

　　上一篇随笔提到了二叉搜索树的删除功能在红黑树中虽然可以用，但会破坏红黑树的结构。

　　其实红黑树的删除功能是在二叉搜索树的删除功能上加上了重构结构的功能。因此，如果不熟悉二叉搜索树的删除功能和红黑树的，建议先看二叉搜索树和红黑树。

2.红黑树的特性

　　在讲删除前，有必要先讲下红黑树的特性。因为我们删除节点后，红黑树的特性应该继续有效。

　　算法导论的原话：

　　1. Every node is either red or black.（每个节点不是红色就是黑色）

　　2. The root is black.（根节点是黑色的）

　　3. Every leaf (NIL) is black.（每个空的节点都是黑色的）

　　4. If a node is red, then both its children are black.（红色节点的子节点都是黑色的）

　　5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.（任意节点到它的子孙节点的路径上，含有的黑节点数目相同）

　　前四条很容易理解，关键是第五条。举个例子：

　　

　　节点19到节点1,5,14,20,30,35的路径都经过了2个黑色节点（不算节点19自己）。

3.删除节点的种类

　　节点可能有0个子节点、1个子节点、2个子节点，再加上节点可分为红色节点和黑色节点，因此总共有6种节点。

　　a. 黑色节点，没子节点。

　　b. 黑色节点，1个子节点。

　　c. 黑色节点，2个子节点。

　　d. 红色节点，没子节点。

　　e. 红色节点，1个子节点。

　　f.  红色节点，2个子节点。

　　但是，在红黑树中，e情况不可能出现，因为要使父节点变为红色，只能通过颜色反转来实现。

　　b情况中，该子节点只能是红色，否则不满足性质5。

　　假设e情况存在，看下图：（由于实际情况下，e情况不可能出现，下面是强行造成e情况存在，故这个红黑树是错误的，不满足性质5：任意节点到它的子孙节点的路径上，含有的黑节点数目相同）

　　

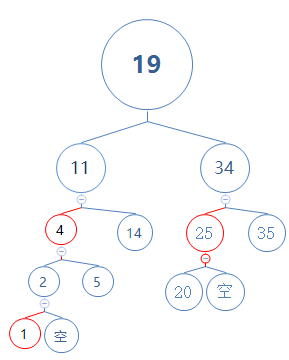
　　我们把目光注视到节点25，这是一个e情况。试想节点20是怎么来的：要么是在节点25之后插入的新节点；要么是删除了节点25的右节点。

　　但是，在即将介绍的删除方法中，不会造成删除了节点25的右节点后，红色节点25只有一个左节点20的情况。　　

　　那么节点20只能是在节点25之后插入的新节点，但是新节点都是红色的，插入时，会变成下图：

　　

　　这样会触发右旋，随后再触发颜色反转、左旋。如下图：

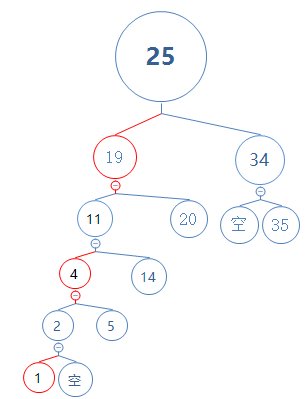　　（由于实际情况下，e情况不可能出现，这里是强行造成e情况存在，故这个红黑树是错误的，不满足性质5：任意节点到它的子孙节点的路径上，含有的黑节点数目相同）

　　因此，在节点25之后插入的新节点20，并不会造成红色节点25只有一个左节点20的情况。故，e情况（e. 红色节点，1个子节点。）不可能出现在红黑树中。

　　请看节点34，这是黑色节点只含有一个黑色子节点的情况。从根节点25到34的左空节点经过了1个黑色节点；从根节点25到节点35经过了2个黑色节点，故不满足性质5，黑色节点只含有一个黑色子节点的情况在红黑树中不存在。

　　综上所述，我们只需要处理的情况有5种：　

　　a. 黑色节点，没子节点。

　　b. 黑色节点，1个红色子节点。

　　c. 黑色节点，2个子节点。

　　d. 红色节点，没子节点。

　　f.  红色节点，2个子节点。

 4.删除节点时的各种情况讨论

一、节点有两个子节点时

　　先讨论情况c和f，即节点有两个子节点。

　　假设要删除节点X，按照二叉搜索树的删除方法，寻找X的后驱继承节点Y。然后除了颜色不变之外，互换X和Y的位置。此时X节点只有一个或没有节点，继续删除它。具体删除方法请看a、b、d情况的删除。

　　举个例子，如下图：

　　

　　假设要删除节点4，则节点5是节点4的后驱继承者。（节点4的右节点中的最小节点。）交换节点5和4，节点颜色不变，如下图：(X=4)

　　

　　继续删除X。此时X是没有子节点的黑色节点，适用于情况a（a. 黑色节点，没子节点。）的删除，下文即将介绍。

二、节点是红色，且没子节点时

　　要讨论的是情况 d. 红色节点，没子节点。直接删除即可。

　　举个例子：

　　

　　如果要删除节点1，节点1属于情况d. 红色节点，没子节点。直接删除，红黑树仍遵守所有特性。

三、节点是黑色，且只有一个红色子节点时

　　要讨论的是情况b（黑色节点，1个红色子节点）。

　　从例子入手：

　　

　　现在要删除节点2。节点2有一个红色节点，直接删除节点2，节点1补上节点2的位置，并且节点1的颜色变为黑色。

　　如下图：

　　

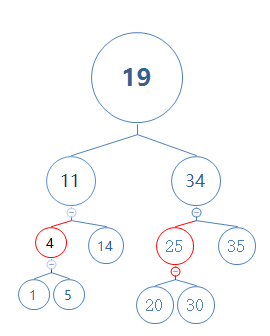
　　即如果要删除含有一个红色子节点的黑色节点，直接删除黑色节点，红色子节点补位，且变为黑色节点。

四、节点是黑色，且没有子节点时

　　要讨论的是情况 a. 黑色节点，没子节点。

　　这里引入一个新节点双重黑色节点（double black），图中用矩形来代表，如下图：

　　

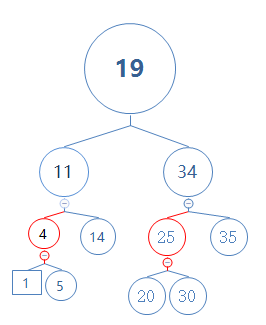
　　节点1为双重黑色节点，双重黑色节点不能存在于红黑树中，我们需要把它变回黑色节点，这样红色树才成立。

　　首先，双重黑色节点怎么产生：当我们要删除一个没有子节点的黑色节点时，就会产生一个双重黑色空节点，且补到删除节点的位置。（还有一种产生方法是在消除双重黑色节点的过程中出现的，稍后介绍。）

 　　举个例子：

　　

　　现在删除节点1，由于节点1是没有子节点的黑色节点，故产生一个双重黑色空节点。如下图：

　　

　　然后，我们接下来讲如何消除双重黑色节点。

消除公式：

　　黑色节点=双重黑色节点+红色节点

　　先介绍邻居节点：假设节点a的两个子节点为节点b和节点c，则节点b是节点c的邻居节点；节点c是节点b的邻居节点

　　

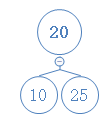
　　如上图，节点10的邻居节点是节点25;节点25的邻居节点是节点10。

　　双重黑色节点出现时，可能面临的情况有：

　　情况1：双重黑色节点的邻居节点是黑色节点，且此邻居节点有一个红色子节点时（最多只能有一个红色子节点，如果有两个，则会触发反转颜色。）

　　情况2：双重黑色节点的邻居节点是黑色节点，且此邻居节点有两个黑色子节点或黑色空子节点时（根据性质5，邻居节点不可能有黑色子节点。因为变成双重黑色节点前，它肯定是一个黑色节点，邻居节点也是黑色节点，如果邻居节点有黑色子节点，则会违反性质5。）

　　情况3：双重黑色节点的邻居节点是红色节点时

　　情况4：双重黑色节点是根节点，没有邻居节点时（如果双重黑色节点不是根节点，不可能没有邻居节点。因为变成双重黑色节点前，它肯定是一个黑色节点，根据性质5，它邻居节点要么是黑色节点，要么是含有两个黑色子节点的红色节点。）

下面将根据各种情况来消除双重黑色节点

情况1：双重黑色节点的邻居节点是黑色节点，且有一个红色子节点时

　　双重黑色节点的邻居节点是黑色节点，且有一个红色子节点的情况如下图：（我们这里的红黑树所有的红色联系都是向左的，所以红色子节点一定为左子节点）

　

　　根据性质5，节点a只能是空节点，节点25只有一个子节点。

　　先对节点23和25进行右旋：

 　　

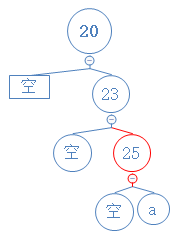
 　　然后对节点20和23进行左旋，红色节点25变为黑色节点，双重黑色空节点变为黑色空节点：

　　

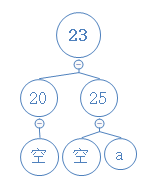
　　消除完毕。

　　上述为邻居节点为右节点时的情形。当邻居节点是左节点时，看下图：

　　

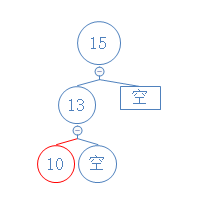
　　对15,13进行右旋，红色节点10变为黑色节点，双重黑色空节点变为黑色空节点：

　　

　　消除完毕。

情况2：双重黑色节点的邻居节点是黑色节点，且有两个黑色空子节点时

当父节点为红色节点时：

　　如下图：

　　

　　请看红色节点4，如果这个节点是反转颜色而来的，那么反转颜色之前是什么样子的呢？

　　逆反转颜色：

　　

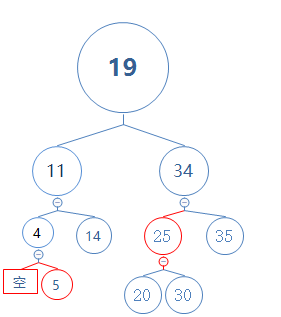
　　这个时候，双重黑色空节点和红色节点重合，相加得黑节点：（黑色节点=双重黑色节点+红色节点）

　　

　　消除完成，触发左旋：

　　

当父节点为黑色节点时：

　　如下图：

　　

　　黑色节点=双重黑色节点+红色节点　　

　　黑色节点5可以看作是双重黑色节点和红色节点的结合体：（这里会产生一个双重黑色节点）

　　

　　然后逆反转颜色：

　　

　　然后双重黑色空节点就消除了。

 　

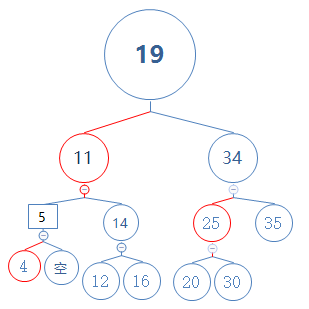
　　 新产生的黑色节点需要根据邻居节点的情况进一步消除。（这里邻居节点的情况是双重黑色节点的邻居节点是黑色节点，且有两个黑色子节点或黑色空子节点，且父节点为红色节点时）

情况3：双重黑色节点的邻居节点是红色节点时

　　这个红色节点肯定是有两个黑色子节点或黑色空子节点。且此红色节点肯定是左节点。（因为在此红黑树中，所有红色节点的都是左节点。）

　　

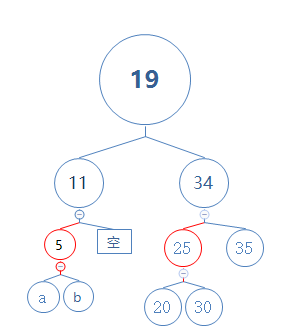
　　节点a,b可能同时为黑色非空节点，也可能是同时为黑色空节点。

　　对节点5和11进行右旋：

　　

　　然后逆反转颜色和消除：

　　

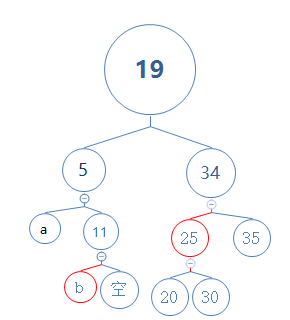
　　消除完毕。

情况4：双重黑色节点是根节点，没有邻居节点时

 　　看下图演变过程：

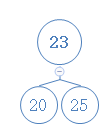　　删除节点20 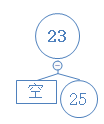双重黑色空节点邻居节点为黑色，且没子节点，消除双重黑色空节点

 　　如果双重黑节点是根节点，直接变成黑色节点即可：

　　

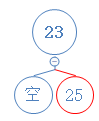
　　触发左旋：

　　

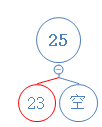
　　至此，所有情况讨论完毕，红黑树删除节点完成。

　　参考文章：https://www.geeksforgeeks.org/red-black-tree-set-3-delete-2/

5.完整代码

节点.h:

UCLASS()
class ALGORITHM_API ARedBlackNode : public AActor
{
    GENERATED_BODY()
    
public:    
    // Sets default values for this actor's properties
    ARedBlackNode();
    // Called every frame
    virtual void Tick(float DeltaTime) override;
    //设值
    FORCEINLINE void SetValue(int Newkey, FString NewValue)
    {
        Key = Newkey;
        Value = NewValue;
    }

    FORCEINLINE ARedBlackNode* Get() { return this; }
    //获取或修改私有变量
    FORCEINLINE int GetKey() { return Key; }
    FORCEINLINE void SetKey(int NewKey) { Key = NewKey; }
    FORCEINLINE int GetCount() { return Count; }
    FORCEINLINE void SetCount(int NewCount) { Count = NewCount; }
    FORCEINLINE FString GetValue() { return Value; }
    FORCEINLINE void SetValue(FString NewValue) { Value = NewValue; }
    FORCEINLINE bool GetColor() { return Color; }
    FORCEINLINE void SetColor(bool IsRed) { Color = IsRed; }
    FORCEINLINE ARedBlackNode* GetParent() { return Parent; }
    FORCEINLINE void SetParent(ARedBlackNode* X) { Parent = X; }
    FORCEINLINE ARedBlackNode* GetNode(bool Left)
    {
        if (Left) return LeftNode;
        return RightNode;
    }
    FORCEINLINE void SetNode(bool Left, ARedBlackNode* NewNode)
    {
        //设定父节点
        if (NewNode)  NewNode->SetParent(this);
        if (Left)  LeftNode = NewNode;
        else RightNode = NewNode;
    }
    //获取邻居节点，用于删除
    FORCEINLINE ARedBlackNode* GetSibling()
    { 
        //如果没父节点，则没邻居节点
        if (!Parent) return nullptr;
        //如果这个节点是父节点的左节点，则邻居节点是父节点的右节点
        if (this == Parent->GetNode(true)) return Parent->GetNode(false);
        //反之则邻居节点是父节点的左节点
        else return Parent->GetNode(true);
    }
    //这个节点有没红色子节点
    FORCEINLINE bool HasRedChild() 
    { 
        return (LeftNode && LeftNode->GetColor() == true) ||
            (RightNode && RightNode->GetColor() == true) ;
    }
    //这个节点是左子节点？
    FORCEINLINE bool IsOnLeft()
    {
        if (!Parent) return false;
        return this == Parent->GetNode(true);
    }

protected:
    // Called when the game starts or when spawned
    virtual void BeginPlay() override;

private:
    int Key;
    FString Value;
    //左右节点
    ARedBlackNode* LeftNode;
    ARedBlackNode* RightNode;
    //父节点，这个节点是为了记录每个节点的位置（用于测试程序是否正确建立红黑树），与红黑树的实现无关。
    ARedBlackNode* Parent;
    //计算此节点下面共有多少个节点（包括自己）
    int Count;
    //与父节点之间的联系，如果为True,则是红色的；如果为False,则是黑色的
    bool Color;
    
};

红黑树.h:

class ARedBlackNode;

UCLASS()
class ALGORITHM_API ARedBlackBST : public AActor
{
    GENERATED_BODY()
    
public:    
    // Sets default values for this actor's properties
    ARedBlackBST();
    // Called every frame
    virtual void Tick(float DeltaTime) override;
    //判断一个节点和它父节点的联系是否是红色的
    bool IsRed(ARedBlackNode* X);
    //查值
    FString GetValue(int InputKey);
    //提供一个方法让TreeNode之间进行比较
    //如果a大于b，返回1；如果a小于b，返回-1；如果相等，返回0
    int CompareTo(int a, int b);
    //向左旋转
    //为什么要左旋：因为在红黑树中，所有红色的联系都是向左的。
    ARedBlackNode* RotateLeft(ARedBlackNode* h);
    //向右旋转
    //为什么要右旋：
    //如果出现连续两个红色联系时（即a,b,c是三个连续的节点，且ab，bc间的联系都是红色的),需要右旋一次
    //然后反转一次颜色，从而符合红黑树的游戏规则。
    ARedBlackNode* RotateRight(ARedBlackNode* h);
    //反转颜色：如果一个节点的左右联系都是红色，则将它们变为黑色，此节点与父节点的联系变为红色
    void FlipColors(ARedBlackNode* h);
    //插入一个节点
    void Put(int Newkey);
    ARedBlackNode* Put(ARedBlackNode* h, int NewKey);
    //中序遍历
    void InorderTraversal();
    void Inorder(ARedBlackNode* X);
    //寻找最小值
    int FindMin();
    //寻找拥有最小值的节点
    ARedBlackNode* FindMin(ARedBlackNode* X);
    //寻找最大值
    int FindMax();
    //寻找拥有最大值的节点
    ARedBlackNode* FindMax(ARedBlackNode* X);
    //给定一个数字，寻找最接近它的key(比它小)
    int FindFloor(int InputKey);
    ARedBlackNode* FindFloor(ARedBlackNode* X, int InputKey);
    //给定一个数字，寻找最接近它的key(比它大)
    int FindCeiling(int InputKey);
    ARedBlackNode* FindCeiling(ARedBlackNode* X, int InputKey);
    
    //求有多少个数字少于给定数字
    int Size(ARedBlackNode* X);
    int Rank(int InputKey);
    int Rank(int InputKey, ARedBlackNode* X);
    //更新各节点路线(先进行层次排序，再更新路线)
    void UpdateRouteString();
    void UpdateRouteString(ARedBlackNode* X);
    //用二叉搜索树删除的方法寻找继承节点(删除某个节点后，这个节点会补位)
    ARedBlackNode* BSTReplace(ARedBlackNode* X);
    //找后驱节点
    ARedBlackNode* Successor(ARedBlackNode* X);
    //删除某个节点
    void DeleteNode(int InputKey);
    void DeleteNode(ARedBlackNode* X);
    //消除双重黑色节点
    void FixDoubleBlack(ARedBlackNode* X);
    //交换两个节点的值
    void SwapKey(ARedBlackNode* X, ARedBlackNode* Y);
    //更新所有父节点的节点数
    void UpdateParentsCount(ARedBlackNode* X);

protected:
    // Called when the game starts or when spawned
    virtual void BeginPlay() override;

private:

    //根节点
    ARedBlackNode* RootNode;
    //每个节点输入的值，可根据具体情况更改，这里只输入空格
    FString FakeValue;
    //把节点接过的路线记录下来，方便测试
    FString RouteString;
    //把节点按中序遍历放进数组
    TArray<ARedBlackNode*> OrderNodeArray;
    //把节点按层次遍历放进数组
    TArray<ARedBlackNode*> LevelOrderNodeArray;
};

红黑树.cpp:

//如果为True,则是红色的；如果为False,则是黑色的
bool Red = true;
bool Black = false;

// Sets default values
ARedBlackBST::ARedBlackBST()
{
     // Set this actor to call Tick() every frame.  You can turn this off to improve performance if you don't need it.
    PrimaryActorTick.bCanEverTick = true;
    FakeValue = "";
}

// Called when the game starts or when spawned
void ARedBlackBST::BeginPlay()
{
    Super::BeginPlay();
    FRandomStream Stream;
    Stream.GenerateNewSeed();
    //生成节点
    for (int i = 0; i < 1000; i++)
    {
        Put(Stream.RandRange(0, 100));
    }
    
    //Put(40);
    Put(19);
    Put(11);
    Put(25);
    Put(4);
    Put(14);
    Put(20);
    Put(35);
    Put(2);
    Put(5);
    Put(30);
    Put(1);
    Put(34);

    //中序排列
    InorderTraversal();
    //观察搜索树是否排列正确
    for (int i = 0; i < OrderNodeArray.Num(); i++)
    {
        UKismetSystemLibrary::PrintString(this, FString::FromInt(i) + ": "
            + FString::FromInt(OrderNodeArray[i]->GetKey())+" "+ OrderNodeArray[i]->GetValue());
    }
    //测试搜索和查值功能
    UKismetSystemLibrary::PrintString(this, "Find 40: " + GetValue(40));
    //测试寻找最小值、最大值、Floor、Ceiling
    UKismetSystemLibrary::PrintString(this, "Min: " + FString::FromInt(FindMin()) +
        " Max: " + FString::FromInt(FindMax()));
    UKismetSystemLibrary::PrintString(this, "Floor of 50: " + FString::FromInt(FindFloor(50)));
    UKismetSystemLibrary::PrintString(this, "Ceiling of 50: " + FString::FromInt(FindCeiling(50)));
    UKismetSystemLibrary::PrintString(this, "Rank(49): "+FString::FromInt(Rank(49)));
    UpdateRouteString();
    for (int i = 0; i < LevelOrderNodeArray.Num(); i++)
    {
        FString Temp;
        if (LevelOrderNodeArray[i]->GetColor()) Temp = "red";
        else Temp = "Black";
        
        UKismetSystemLibrary::PrintString(this, FString::FromInt(i) + ": "
            + FString::FromInt(LevelOrderNodeArray[i]->GetKey()) + " " + LevelOrderNodeArray[i]->GetValue()
            + " Count: " + FString::FromInt(LevelOrderNodeArray[i]->GetCount()) + " Color:" + Temp);
        //if (LevelOrderNodeArray[i]->GetKey() == 2)
        //{
        //    //测试寻找邻居节点和是否有红色子节点
        //    UKismetSystemLibrary::PrintString(this, "Sibling: " + FString::FromInt(LevelOrderNodeArray[i]->GetSibling()->GetKey())
        //        + " HasRedChild: " + UKismetStringLibrary::Conv_BoolToString(LevelOrderNodeArray[i]->HasRedChild()));
        //    //测试寻找继承节点
        //    if (BSTReplace(LevelOrderNodeArray[i]))
        //    {
        //        UKismetSystemLibrary::PrintString(this, FString::FromInt(BSTReplace(LevelOrderNodeArray[i])->GetKey()));
        //    }
        //    else UKismetSystemLibrary::PrintString(this, "BSTReplace Not Exist");
        //}
    }

    //测试删除
    UKismetSystemLibrary::PrintString(this, "StartDelete!");
    DeleteNode(14);
    DeleteNode(34);
    DeleteNode(4);
    DeleteNode(11);
    DeleteNode(35);
    DeleteNode(RootNode);
    UpdateRouteString();
    for (int i = 0; i < LevelOrderNodeArray.Num(); i++)
    {
        FString Temp;
        if (LevelOrderNodeArray[i]->GetColor()) Temp = "red";
        else Temp = "Black";

        UKismetSystemLibrary::PrintString(this, FString::FromInt(i) + ": "
            + FString::FromInt(LevelOrderNodeArray[i]->GetKey()) + " " + LevelOrderNodeArray[i]->GetValue()
            + " Count: " + FString::FromInt(LevelOrderNodeArray[i]->GetCount()) + " Color:" + Temp);
    }
}

// Called every frame
void ARedBlackBST::Tick(float DeltaTime)
{
    Super::Tick(DeltaTime);
}

//判断一个节点和它父节点的联系是否是红色的
bool ARedBlackBST::IsRed(ARedBlackNode* X)
{
    if (!X) return false;
    return X->GetColor() == Red;
}

FString ARedBlackBST::GetValue(int InputKey)
{
    ARedBlackNode* X = RootNode;
    while (X != nullptr)
    {
        //比较key的大小
        int Temp = CompareTo(InputKey, X->GetKey());
        //如果输入的key比X的小，去X的左边
        if (Temp < 0) X = X->GetNode(true);
        //如果输入的key比X的大，去X的右边
        else if (Temp > 0) X = X->GetNode(false);
        //如果相等，说明找到这个key了，输出Value
        else return X->GetValue();
    }
    //如果X为空指针，说明找不到这个key
    return "NotFind";
}

//如果a大于b，返回1；如果a小于b，返回-1；如果相等，返回0
int ARedBlackBST::CompareTo(int a, int b)
{
    if (a > b) return 1;
    else if (a < b) return -1;
    else return 0;
}

ARedBlackNode* ARedBlackBST::RotateLeft(ARedBlackNode* h)
{
    //X节点是h的右节点。
    //左旋的结果是:
    //1.X成为了h的父节点，h是X的左节点。
    //2.X原来的左节点变成了h的右节点,其它节点不变，h和X之间的联系还是红色。
    //如果旋转前，h是根节点，则旋转后，X是根节点，X没父节点
    bool HIsRoot = h == RootNode;
    
    ARedBlackNode* X = h->GetNode(false);
    //ARedBlackNode* Parent = h->GetParent();
    h->SetNode(false, X->GetNode(true));
    X->SetNode(true, h);
    //如果X节点是红色节点，则左旋后，h是红色节点，X是黑色节点
    if (X->GetColor() == Red)
    {
        X->SetColor(h->GetColor());
        h->SetColor(Red);
    }
    
    //左旋后，两节点的Count更新
    h->SetCount(1 + Size(h->GetNode(false)) + Size(h->GetNode(true)));
    X->SetCount(1 + Size(X->GetNode(false)) + Size(X->GetNode(true)));
    UKismetSystemLibrary::PrintString(this, "RotateLeft");
    if (HIsRoot)
    {
        X->SetParent(nullptr);
        RootNode = X;
    }

    return X;
}

ARedBlackNode* ARedBlackBST::RotateRight(ARedBlackNode* h)
{
    //X节点是h的左节点。
    //左旋的结果是:
    //1.X成为了h的父节点，h是X的右节点。
    //2.X原来的右节点变成了h的左节点,其它节点不变，h和X之间的联系还是红色。
    //如果旋转前，h是根节点，则旋转后，X是根节点，X没父节点
    bool HIsRoot = h == RootNode;
    ARedBlackNode* X = h->GetNode(true);
    //ARedBlackNode* Parent = h->GetParent();
    h->SetNode(true, X->GetNode(false));
    X->SetNode(false, h);
    //如果X节点是红色节点，则右旋后，h是红色节点，X是黑色节点
    if (X->GetColor() == Red)
    {
        X->SetColor(h->GetColor());
        h->SetColor(Red);
    }
    //右旋后，两节点的Count更新
    h->SetCount(1 + Size(h->GetNode(false)) + Size(h->GetNode(true)));
    X->SetCount(1 + Size(X->GetNode(false)) + Size(X->GetNode(true)));
    UKismetSystemLibrary::PrintString(this, "RotateRight");
    if (X == RootNode) X->SetParent(nullptr);
    if (HIsRoot)
    {
        X->SetParent(nullptr);
        RootNode = X;
    }
    return X;
}

void ARedBlackBST::FlipColors(ARedBlackNode* h)
{
    //反转颜色：如果一个节点的左右联系都是红色，则将它们变为黑色，此节点与父节点的联系变为红色
    h->SetColor(Red);
    h->GetNode(true)->SetColor(Black);
    h->GetNode(false)->SetColor(Black);
    h->SetValue("");
}

void ARedBlackBST::Put(int Newkey)
{
    RootNode = Put(RootNode, Newkey);
    //根节点必须是黑色的
    RootNode->SetColor(Black);
}

ARedBlackNode* ARedBlackBST::Put(ARedBlackNode* h, int NewKey)
{
    if (!h)
    {
        ARedBlackNode* NewNode = GetWorld()->SpawnActor<ARedBlackNode>(ARedBlackNode::StaticClass());
        NewNode->SetValue(NewKey, FakeValue);
        //新节点与父节点的联系一开始是红色的（后续可能会经过旋转，反转等操作，变成黑色）
        NewNode->SetColor(Red);
        NewNode->SetCount(1);
        return NewNode;
    }
    //与二叉搜索树相同，如果新节点的key比h节点的key小，则去h节点的左边；如果大，则去右边；如果相同，则覆盖h节点
    int Temp = CompareTo(NewKey, h->GetKey());
    //如果要插入新节点，则新节点的所有父节点都要更新一次
    if (Temp < 0) h->SetNode(true, Put(h->GetNode(true), NewKey));
    else if (Temp > 0) h->SetNode(false, Put(h->GetNode(false), NewKey));
    else h->SetValue(FakeValue);
    //更新h节点的Count
    h->SetCount(1 + Size(h->GetNode(true)) + Size(h->GetNode(false)));

    //h与右节点联系是红色的，且与左节点的联系是黑色的，则需要左旋
    if (IsRed(h->GetNode(false)) && !IsRed(h->GetNode(true))) h = RotateLeft(h);
    //如果h与左节点的联系是红色的，且h与左节点的左节点的联系也是红色的，说明出现连续两个红色联系，需要右旋
    if (IsRed(h->GetNode(true)) && IsRed(h->GetNode(true)->GetNode(true))) h = RotateRight(h);
    //如果h节点的左右联系都是红色，则需要反转（注意：根节点的反转只会把它们变为黑色，因为它没有父节点）
    if (IsRed(h->GetNode(true)) && IsRed(h->GetNode(false))) FlipColors(h);
    //以上三种情况排序是故意的，因为左旋后可能需要右旋，右旋后需要反转
    //以上三种情况可能会分别触发，也可能会连续触发

    //给左右子节点设置父节点
    //if (h->GetNode(true)) h->GetNode(true)->SetParent(h);
    //if (h->GetNode(false)) h->GetNode(false)->SetParent(h);
    
    return h;
}

void ARedBlackBST::InorderTraversal()
{
    OrderNodeArray.Empty();
    Inorder(RootNode);
}

void ARedBlackBST::Inorder(ARedBlackNode* X)
{
    if (!X) return;
    //先去加X的左节点
    Inorder(X->GetNode(true));
    //再加X
    OrderNodeArray.Add(X);
    //最后加X的右节点
    Inorder(X->GetNode(false));
}

int ARedBlackBST::FindMin()
{
    //从根节点开始比较
    ARedBlackNode* X = FindMin(RootNode);
    if (X) return X->GetKey();
    return 0;
}

ARedBlackNode* ARedBlackBST::FindMin(ARedBlackNode* X)
{
    //当节点存在时
    while (X)
    {
        //如果左节点存在，继续循环
        if (X->GetNode(true))
        {
            X = X->GetNode(true);
        }
        //如果右节点不存在，这个节点就是最小值
        else
        {
            return X;
        }
    }
    return X;
}

int ARedBlackBST::FindMax()
{
    //从根节点开始比较
    ARedBlackNode* X = FindMax(RootNode);
    if (X) return X->GetKey();
    return 0;
}

ARedBlackNode* ARedBlackBST::FindMax(ARedBlackNode* X)
{
    //当节点存在时
    while (X)
    {
        //如果右节点存在，继续循环
        if (X->GetNode(false))
        {
            X = X->GetNode(false);
        }
        //如果右节点不存在，这个节点就是最小值
        else
        {
            return X;
        }
    }
    return X;
}

int ARedBlackBST::FindFloor(int InputKey)
{
    //从根节点开始比较
    ARedBlackNode* X = FindFloor(RootNode, InputKey);
    if (X) return X->GetKey();
    return 0;
}

ARedBlackNode* ARedBlackBST::FindFloor(ARedBlackNode* X, int InputKey)
{
    //如果X节点不存在，就别继续下去了
    if (!X) return nullptr;
    int Temp = CompareTo(InputKey, X->GetKey());
    //如果存在节点的key与输入值相等，则这个节点就是最接近它了
    if (Temp == 0) return X;
    //如果节点的key比较大，则去找它的左节点，直到找到小于等于输入值的节点为止
    if (Temp < 0) return FindFloor(X->GetNode(true), InputKey);
    //如果节点的key比较小，则要找的节点可能在它的右节点的左端
    ARedBlackNode* T = FindFloor(X->GetNode(false), InputKey);
    //如果找到了T,则说明找到了，返回T;如果找不到，说明X已经是最接近的了，返回X
    if (T) return T;
    else return X;
}

int ARedBlackBST::FindCeiling(int InputKey)
{
    //从根节点开始比较
    ARedBlackNode* X = FindCeiling(RootNode, InputKey);
    if (X) return X->GetKey();
    return 0;
}

ARedBlackNode* ARedBlackBST::FindCeiling(ARedBlackNode* X, int InputKey)
{
    //如果X节点不存在，就别继续下去了
    if (!X) return nullptr;
    int Temp = CompareTo(InputKey, X->GetKey());
    //如果存在节点的key与输入值相等，则这个节点就是最接近它了
    if (Temp == 0) return X;
    //如果节点的key比较小，则去找它的右节点，直到找到大于等于输入值的节点为止
    if (Temp > 0) return FindCeiling(X->GetNode(false), InputKey);
    //如果节点的key比较大，则要找的节点可能在它的左节点的左端
    ARedBlackNode* T = FindCeiling(X->GetNode(true), InputKey);
    //如果找到了T,则说明找到了，返回T;如果找不到，说明X已经是最接近的了，返回X
    if (T) return T;
    else return X;
}

int ARedBlackBST::Size(ARedBlackNode* X)
{
    //如果节点不存在，返回0
    if (!X) return 0;
    //如果节点存在，返回Count
    return X->GetCount();
}

int ARedBlackBST::Rank(int InputKey)
{
    return Rank(InputKey, RootNode);
}

int ARedBlackBST::Rank(int InputKey, ARedBlackNode* X)
{
    //如果节点不存在，返回0
    if (!X) return 0;
    int Temp = CompareTo(InputKey, X->GetKey());
    //如果给定数字比X的key小，则去X的左边去找比给定数字小的数字
    if (Temp < 0) return Rank(InputKey, X->GetNode(true));
    //如果给定数字比X的key大，则X和X的左节点都比给定数字小，把它们算上后，去X的右节点找是否还有比给定数字小的数字
    else if (Temp > 0) return 1 + Size(X->GetNode(true)) + Rank(InputKey, X->GetNode(false));
    //因为右节点都比X大，而X的Key与给定数字相等，故比给定数字小的数字都在X的左节点里
    else return Size(X->GetNode(true));
}

void ARedBlackBST::UpdateRouteString()
{
    RouteString = "";
    LevelOrderNodeArray.Empty();
    UpdateRouteString(RootNode);
    //RootNode->SetValue("Root");
}

void ARedBlackBST::UpdateRouteString(ARedBlackNode* X)
{
    TQueue<ARedBlackNode*> q;
    q.Enqueue(RootNode);
    while (!q.IsEmpty())
    {
        ARedBlackNode* T;
        q.Dequeue(T);
        LevelOrderNodeArray.Add(T);
        //如果T的父节点存在
        if (T->GetParent())
        {
            //如果T是左节点
            if (T == T->GetParent()->GetNode(true))
            {
                FString TempString;
                TempString.Append(T->GetParent()->GetValue());
                TempString.Append("->Left");
                T->SetValue(TempString);
            }
            //如果T是右节点
            else if (T == T->GetParent()->GetNode(false))
            {
                FString TempString;
                TempString.Append(T->GetParent()->GetValue());
                TempString.Append("->Right");
                T->SetValue(TempString);
            }
            else
            {
                T->SetValue("Root");
            }
        }
        //如果父节点不存在，说明是根节点
        else
        {
            T->SetValue("Root");
        }

        //将出队的左节点入队
        if (T->GetNode(true))
        {
            //T->GetNode(true)->SetParent(T);
            q.Enqueue(T->GetNode(true));
        }
        //将出队的右节点入队
        if (T->GetNode(false))
        {
            //T->GetNode(false)->SetParent(T);
            q.Enqueue(T->GetNode(false));
        }
    }
}

ARedBlackNode* ARedBlackBST::BSTReplace(ARedBlackNode* X)
{
    //如果X节点有两个子节点，返回后驱节点
    if (X->GetNode(true) && X->GetNode(false)) return Successor(X->GetNode(false));
    //如果X节点没有子节点，返回空
    else if (!X->GetNode(true) && !X->GetNode(false)) return nullptr;
    //如果X节点只有一个左节点
    else if (X->GetNode(true)) return X->GetNode(true);
    //如果X节点只有一个右节点
    else return X->GetNode(false);
}

ARedBlackNode* ARedBlackBST::Successor(ARedBlackNode* X)
{
    //后驱节点是X节点下面的最小节点，它没有左节点
    ARedBlackNode* Temp = X;
    while (Temp->GetNode(true)) Temp = Temp->GetNode(true);
    return Temp;
}

void ARedBlackBST::DeleteNode(ARedBlackNode* X)
{
    //继承节点
    ARedBlackNode* u = BSTReplace(X);
    //u和x都是黑色节点吗？
    bool uxBlack = ((!u || u->GetColor() == Black) && (X->GetColor() == Black));
    ARedBlackNode* Parent = X->GetParent();
    //如果继承节点u不存在，说明节点X没子节点
    if (!u)
    {
        //如果X是根节点，说明想删根节点，且根节点下面没节点
        if (X == RootNode) RootNode = nullptr;
        //X是普通节点
        else
        {
            //如果u,x都是黑色节点，且X没子节点，那么删除它将产生双重黑色节点，需要消除它
            if (uxBlack)
            {
                //删除后，节点数更新
                Parent->SetCount(Parent->GetCount() - 1);
                UpdateParentsCount(Parent);
                //X还没删除，X的节点数设为0
                X->SetCount(0);
                FixDoubleBlack(X);
            }
            //如果uxBlack==false,说明X节点是红色的，且没子节点，直接删除
            else
            {
                //删除后，节点数更新
                Parent->SetCount(1);
                UpdateParentsCount(Parent);
            }
            //删除这个节点后，父节点把这个节点清空
            if (X->IsOnLeft()) Parent->SetNode(true, nullptr);
            else Parent->SetNode(false, nullptr);
        }
        //删除节点
        X->Destroy();
        return;
    }
    //如果X只有一个子节点，那么只有一种可能性：X是黑色节点，u是红色节点
    if (!X->GetNode(true) || !X->GetNode(false))
    {
        //如果X是根节点，且只有一个节点，直接删除，子节点成为根节点
        //这里是把子节点的值和X的值互换，然后删除子节点u
        if (X == RootNode)
        {
            X->SetKey(u->GetKey());
            //删除后，没有子节点了
            X->SetNode(true, nullptr);
            X->SetNode(false, nullptr);
            u->Destroy();
            //更新节点数
            X->SetCount(1);
        }
        //如果X不是根节点,直接删除X节点，u节点补位，并变成黑色节点
        else
        {
            //子节点u补位
            if (X->IsOnLeft()) Parent->SetNode(true, u);
            else Parent->SetNode(false, u);
            X->Destroy();
            u->SetParent(Parent);
            u->SetColor(Black);
            //u的节点数是正确的，不用更新
            //更新U的所有父节点的节点数
            UpdateParentsCount(u);
            
        }
        return;
    }

    //如果来到这，说明X有两个子节点，交换u,x的值，继续删除u节点
    SwapKey(X, u);
    DeleteNode(u);
}

void ARedBlackBST::DeleteNode(int InputKey)
{
    //先找到这个节点
    ARedBlackNode* X = RootNode;
    while (X != nullptr)
    {
        //比较key的大小
        int Temp = CompareTo(InputKey, X->GetKey());
        //如果输入的key比X的小，去X的左边
        if (Temp < 0) X = X->GetNode(true);
        //如果输入的key比X的大，去X的右边
        else if (Temp > 0) X = X->GetNode(false);
        //如果相等，说明找到这个节点了,跳出循环
        else break;
    }
    //如果X不存在，说明要删除的节点不存在
    if (!X) UKismetSystemLibrary::PrintString(this, "Not Such Node!");
    //如果存在，进行删除
    DeleteNode(X);
}

void ARedBlackBST::FixDoubleBlack(ARedBlackNode* X)
{
    //如果X是双重黑色根节点，说明此时X有一个红色子节点，如果是右红色子节点，需要左旋。随后返回
    if (X == RootNode)
    {
        if (X->GetNode(false)) RotateLeft(X);
        return;
    }
    //获取X的邻居节点和父节点
    ARedBlackNode* Sibling = X->GetSibling();
    ARedBlackNode* Parent = X->GetParent();
    //如果X不是根节点，则不可能没有邻居节点和父节点
    if (!Sibling) return;
    if (!Parent) return;
    //如果邻居节点是红色节点，那么此节点肯定是左节点，右旋
    if (Sibling->GetColor() == Red)
    {
        //父节点的父节点
        ARedBlackNode* GrandParent = Parent->GetParent();
        //如果祖父节点存在，需要更新节点联系
        if (GrandParent)
        {
            //如果父节点是左节点，把旋转后的节点放回祖父节点的左节点处
            if (Parent->IsOnLeft()) GrandParent->SetNode(true, RotateRight(Parent));
            //反之，则放回祖父节点的右节点处
            else GrandParent->SetNode(false, RotateRight(Parent));
        }
        //如果祖父节点不存在，说明父节点是根节点，不需要更新祖父节点
        else RotateRight(Parent);

        //为了消除双重黑色节点，逆反转颜色
        Parent->SetColor(Black);
        //右旋之后，如果Parent的左子节点存在，把它变红
        if (Parent->GetNode(true)) Parent->GetNode(true)->SetColor(Red);
        return;
    }
    //邻居节点是黑色
    else
    {
        //邻居节点有红色子节点，这个节点肯定是左节点
        if (Sibling->HasRedChild())
        {
            //邻居节点是左节点时
            if (Sibling->IsOnLeft())
            {
                //子节点变为黑色节点
                Sibling->GetNode(true)->SetColor(Black);
                //记录父节点是不是红色的
                bool RedParent = Parent->GetColor() == Red;
                //旋转前，把父节点的颜色变为黑色
                Parent->SetColor(Black);
                //父节点的父节点
                ARedBlackNode* GrandParent = Parent->GetParent();
                //如果祖父节点存在，需要更新节点联系
                if (GrandParent)
                {
                    //如果父节点是左节点，把旋转后的节点放回祖父节点的左节点处
                    if (Parent->IsOnLeft()) GrandParent->SetNode(true, RotateRight(Parent));
                    //反之，则放回祖父节点的右节点处
                    else GrandParent->SetNode(false, RotateRight(Parent));
                }
                //如果祖父节点不存在，说明父节点是根节点，不需要更新祖父节点
                else RotateRight(Parent);
                //如果旧父节点是红色的，则成为了新父节点的邻居节点也应该是红色的
                if (RedParent) Sibling->SetColor(Red);
            }
            //邻居节点是右节点时
            else
            {
                //记录父节点是不是红色的
                bool RedParent = Parent->GetColor() == Red;
                //把红色子节点记录下来，最后消除完毕时，此节点变成了父节点
                ARedBlackNode* RedChild = Sibling->GetNode(true);
                //旋转前，把父节点的颜色变为黑色
                Parent->SetColor(Black);
                //Sibling->GetNode(true)->SetColor(Parent->GetColor());
                //先对邻居节点右旋,右旋后，邻居节点变成了红色节点
                Parent->SetNode(false, RotateRight(Sibling));
                //红色节点变回黑色节点
                Sibling->SetColor(Black);
                //再对父节点左旋，注意，这里的左旋中，父节点的右节点是黑色节点，左旋后，它们还是黑色节点
                //父节点的父节点
                ARedBlackNode* GrandParent = Parent->GetParent();
                //如果祖父节点存在，需要更新节点联系
                if (GrandParent)
                {
                    //如果父节点是左节点，把旋转后的节点放回祖父节点的左节点处
                    if (Parent->IsOnLeft()) GrandParent->SetNode(true, RotateLeft(Parent));
                    //反之，则放回祖父节点的右节点处
                    else GrandParent->SetNode(false, RotateLeft(Parent));
                }
                //如果祖父节点不存在，说明父节点是根节点，不需要更新祖父节点
                else RotateLeft(Parent);
                //如果旧父节点是红色的，则新父节点也应该是红色的
                if (RedParent) RedChild->SetColor(Red);
            }
        }
        //邻居节点有两个黑色子节点或没有子节点时
        else
        {
            //进行逆反转颜色
            //不管父节点是否是红色节点，邻居节点都会变成红色节点
            Sibling->SetColor(Red);
            //如果父节点是红色节点，直接变成黑色节点
            if (Parent->GetColor() == Red) Parent->SetColor(Black);
            //如果父节点是黑色节点，变成双重黑色节点，继续消除它
            FixDoubleBlack(Parent);
        }
    }
}

//交换两个节点的值
void ARedBlackBST::SwapKey(ARedBlackNode* X, ARedBlackNode* Y)
{
    int Temp;
    Temp = X->GetKey();
    X->SetKey(Y->GetKey());
    Y->SetKey(Temp);
}

void ARedBlackBST::UpdateParentsCount(ARedBlackNode* X)
{
    if (!X) return;
    //X的所有父节点都要更新节点数
    ARedBlackNode* G = X->GetParent();
    while (G)
    {
        G->SetCount(1 + Size(G->GetNode(true)) + Size(G->GetNode(false)));
        G = G->GetParent();
        
    }
}