算法之搜索

搜索顾名思义，就是一个个地寻找，直到寻找到最优解或者答案为止

搜索经常和递归和栈相关，因为我们需要遍历每个地方的，不管这个分支是否有解都要回溯一下

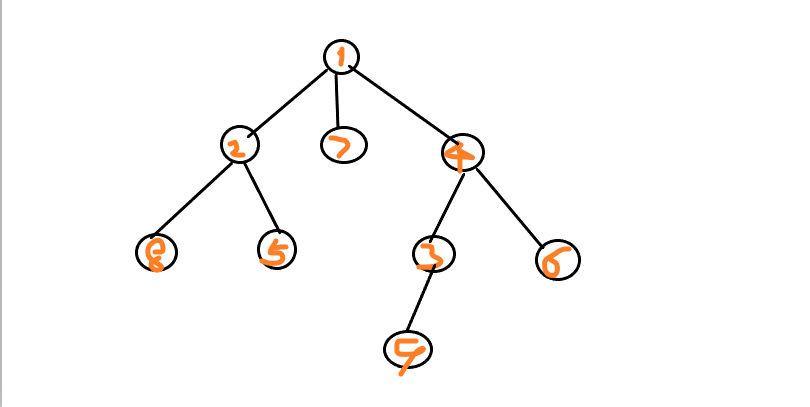
首先我们先熟悉树和图的遍历：

1.存储方式，选择邻接表；这样是很省空间的

邻接表，以表头数组head,使用ver和edge数组分别表示这一条边的终点和权值，使用next数组模拟链表指针

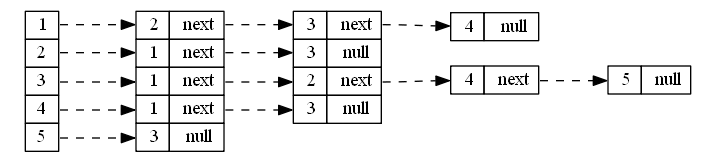
 以一个有向图为例：

x,y,z分别表示起点和终点，该边的权值

const int N = 1e3 + 10;
int head[N],edge[N],ver[N],next[N];

int tot = 0;

void add(int x,int y,int z){//添加一条边 
	ver[++tot] = y; edge[tot] = z;
	next[tot] = head[x],head[x] = tot;
}

　　给出遍历一个有向图的demo

#include<bits/stdc++.h>
using namespace std; 

const int N = 1e3 + 10;
int head[N],edge[N],ver[N],nex[N];
bool vis[N];
int tot = 0;

void add(int x,int y,int z){//添加一条边 
	ver[++tot] = y; edge[tot] = z;
	nex[tot] = head[x],head[x] = tot;
}

void dfs(int x){
	cout << x << " ";
	vis[x] = 1;
	for(int i = head[x];i;i = nex[i]){
		int y = ver[i];
		if(!vis[y]) dfs(y);
	}
}

int main(){
	int n,m;
	int x,y,z;
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		cin >> x >> y >> z;
		add(x,y,z); 
	}
	dfs(1);
	return 0;
}

　　关于树的还有一些信息需要我们去找出来，然后也使用深度优先去找的

时间戳：每个结点第一次被访问到时是第几个被访问的

给出代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;

int head[N],nex[N],ver[N],dfsn[N],d[N];
bool vis[N];
int tot = 0,cur = 0;

void add(int x,int y){
	d[y]++;
	ver[++tot] = y;
	nex[tot] = head[x],head[x] = tot;
}

void dfs(int x){
	vis[x] = 1;
	dfsn[++cur] = x;
	for(int i = head[x]; i ; i = nex[i]){
		int y = ver[i];
		if(!vis[y]) dfs(y);
	} 
}

int main ()
{
	int n,m,x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		cin >> x >> y;
		add(x,y);
	}
	
	for(int i = 1;i <= n;i++)
	if(d[i] == 0){
		dfs(i);
		break;
	}
	
	for(int i = 1;i <= n; i ++)
	cout << dfsn[i] << " ";
	puts("");
	return 0;
}

　　dfs序：就是刚进入递归和回溯是记录该点的编号，最后产生2*N的序列(假设有N个点)，同时两个相同数字的序列区间就是一颗子树

 给出代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;

int head[N],nex[N],ver[N],dfsn[N],d[N];
bool vis[N];
int tot = 0,cur = 0;

void add(int x,int y){
	d[y]++;
	ver[++tot] = y;
	nex[tot] = head[x],head[x] = tot;
}

void dfs(int x){
	vis[x] = 1;
	dfsn[++cur] = x;
	for(int i = head[x]; i ; i = nex[i]){
		int y = ver[i];
		if(!vis[y]) dfs(y);
	} 
	dfsn[++cur] = x;
}

int main ()
{
	int n,m,x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		cin >> x >> y;
		add(x,y);
	}
	
	for(int i = 1;i <= n;i++)
	if(d[i] == 0){
		dfs(i);
		break;
	}
	
	for(int i = 1;i <= n*2
	; i ++)
	cout << dfsn[i] << " ";
	puts("");
	return 0;
}

　　树的深度，我们假设根节点的深度是0，我们直到假设y是x的子节点则 d[y] = d[x] + 1 dfs就可以知道了深度一样代表这些结点在一层

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;

int head[N],nex[N],ver[N],dfsn[N],d[N],depth[N];
bool vis[N];
int tot = 0,cur = 0;

void add(int x,int y){
	d[y]++;
	ver[++tot] = y;
	nex[tot] = head[x],head[x] = tot;
}

void dfs(int x){
	vis[x] = 1;
	for(int i = head[x]; i ; i = nex[i]){
		int y = ver[i];
		if(!vis[y]) {
			depth[y] = depth[x] + 1;
			dfs(y);
		}
	} 
}

int main ()
{
	int n,m,x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		cin >> x >> y;
		add(x,y);
	}
	
	for(int i = 1;i <= n;i++)
	if(d[i] == 0){
		dfs(i);
		break;
	}
	
	for(int i = 1;i <= n; i ++)
	cout << i << " " << depth[i] << endl;
	return 0;
}

　　

我们记size[i]为以i为根节点的这个树包含的结点数量，包括本节点

树的重心：去掉该节点，然后剩下的子树中最大的size[i]相比去掉其他结点j后剩下的子树中最大的size[j]是最小的

对于结点i它的size等于所有儿子的size加上自己1

#include<bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;

int head[N],ver[N],nex[N],size[N],ig[N];

bool vis[N];
int ans,pos,tot = 0;
int n,m;

void add(int x,int y){
	ver[++tot] = y;
	ig[y]++;
	nex[tot] = head[x]; head[x] = tot;
}

void dfs(int x){
	vis[x] = 1;
	size[x] = 1;
	int max_part = 0;
	for(int i = head[x]; i ; i = nex[i]){
		int y = ver[i];
		if(!vis[y]){
			dfs(y);
			size[x] += size[y];
			max_part  = max(max_part,size[y]);
		}
	}
	
	max_part = max(max_part,n - size[x]);
	if(max_part < ans){
		ans = max_part;
		pos = x;
	}
}

int main(){
	
	int x,y;
	cin >> n >> m;
	ans = n + 1;
	for(int i = 1;i <= m;i++){
		cin >> x >> y;
		add(x,y);
	}
	
	for(int i = 1;i <= n;i++)
	if(!ig[i]){
		dfs(i);
		break;
	}
	
	puts("");
	for(int i = 1;i <= n;i++)
	cout << i << " " << size[i] << endl;
	
	cout << pos << " " << ans << endl;
	return 0;
}

　　dfs还可以统计无向图有多少联通块，在main()函数中

int cnt = 0;
	for(int i = 1;i <= n;i++)
	if(!vis[i]) {
		dfs(i);
		cnt++;
	}

　　
下面说一下广度优先搜索bfs

广度就是一层层遍历，先遍历入度为0的节点，需要用到队列

#include<bits/stdc++.h>
using namespace std;

const int N = 1e3 + 10;
int head[N],ver[N],nex[N],d[N];

int tot = 0;
void add(int x,int y){
	ver[++tot] = y;
	nex[tot] = head[x];
	head[x] = tot;
}

void bfs(){
	queue<int> q;
	q.push(1); d[1] = 1;
	
	while(q.size()){
		int cur = q.front(); q.pop();
		cout << cur << " ";
		for(int i = head[cur]; i ; i = nex[i]){
			int y = ver[i];
			if(d[y]) continue;
			d[y] = d[cur] + 1;
			q.push(y);
		}
	}
	puts("");
}

int main(){
	int n,m,x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		cin >> x >> y;
		add(x,y);
	}
	bfs();
	
	return 0;
}

　　拓扑排序：就是这些结点的遍历是有顺序的，必须有先后关系

#include<bits/stdc++.h>
using namespace std;

const int N = 1e3 + 10;
int ver[N],head[N],nex[N],ig[N];

int tot = 0,n,m;

void add(int x,int y){
	ver[++tot] = y;
	ig[y]++;
	nex[tot] = head[x];
	head[x] = tot;
}

void topsort(){
	queue<int> q;
	for(int i = 1;i <= n;i++){
		if(!ig[i]) q.push(i);
	}
	
	while(q.size()){
		int cur = q.front(); q.pop();
		cout << cur << " ";
		for(int i = head[cur]; i ; i = nex[i]){
			int y = ver[i];
			if(--ig[y] == 0) q.push(y);
		} 
	}
	puts("");
}

int main(){
	int x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		cin >> x >> y;
		add(x,y);
	}
	topsort();
	return 0;
}

　　接下来做几个题来看看吧

给定一张N个点M条边的有向无环图，分别统计从每个点出发能够到达的点的数量。

输入格式

第一行两个整数N,M，接下来M行每行两个整数x,y，表示从x到y的一条有向边。

输出格式

输出共N行，表示每个点能够到达的点的数量。

1 <= N,M <= 30000

输入样例：

10 10
3 8
2 3
2 5
5 9
5 9
2 3
3 9
4 8
2 10
4 9

输出样例：

1
6
3
3
2
1
1
1
1
1


要知道每个结点所能到达的点个数，我们必须先知道它的所有儿子的访达数，然后取一个并集

那么我们必须先知道儿子，这个时候可以用拓扑排序，这样会先访问父节点，那么得到的访问序列的逆序不就可以先儿子后父亲了吗
不过这个地方有个坑，就是空间给你的限制，要用到bitset 里面的元素只占1bit,如果用bool数组每个元素占一个字节b倍的关系
取并集就或就好了

#include<bits/stdc++.h>
using namespace std;
const int N = 3e4 + 10;

int head[N],ver[N],a[N],ig[N],nex[N];

bitset<N> bs[N];
int tot = 0,n,m,cnt = 0;

void add(int x,int y){
	ver[++tot] = y;
	ig[y]++;
	nex[tot] = head[x];
	head[x] = tot;
}

void topsort(){
	queue<int> q;
	for(int i = 1;i <= n;i++)
	if(!ig[i]) q.push(i);
	
	while(q.size()){
		int cur = q.front(); q.pop();
		a[++cnt] = cur;
		for(int i = head[cur]; i ; i = nex[i]){
			int y = ver[i];
			if(--ig[y] == 0) q.push(y);
		}
	}
}

int main(){
	int x,y;
	cin >> n >> m;
	for(int i = 1;i <= m;i++){
		cin >> x >> y;
		add(x,y);
	}
	
	topsort();
	//reverse(a+1,a+cnt+1);
	for(int i = cnt;i >= 1;i--){
		int cur = a[i];
		bs[cur][cur] = 1;
		for(int j = head[cur]; j ; j = nex[j]){
			int y = ver[j];
			bs[cur] |= bs[y];//取交集，因为有可能二者有一个共同的儿子结点 
		}
	}
	
	for(int i = 1;i <= n; i ++)
	cout << bs[i].count() << endl; 
	return 0;
}

　　

2.小猫爬山

有N只小猫，每只小猫的重量c[i],每个缆车的承载量W。 c[i] <= W <= 1e8,N <= 18

为最小需要多少个缆车能把它们从一边运到另一边

我们需要确定猫怎样分配在哪一辆车才是最优的？

所以就得搜索，搜索的时候需要记录每一辆缆车当前的剩余容量，以及当前要装的是第几只猫

对于当前的猫，如果有某一量车的剩余容量大于等于它的重量，有两种选择，要么放入这辆车，要么装入新的没有其他猫的车

然后当搜索完之后更新答案即可

为了加快搜索，我们可以先放入重量比较大的猫，这样之后当前这辆车剩余容量小，可决策的数量少。需要搜索的就少

还有一个优化就是如果当前的车数量比得到的答案大于等于直接回溯就好了

#include<bits/stdc++.h>
using namespace std;

const int N = 20;
int c[N],cab[N],w,n;
int ans;

void dfs(int cur,int cnt){
	if(cnt >= ans) return;
	if(cur == n + 1){
		ans = min(ans,cnt);
		return;
	}
	
	for(int i = 1;i <= cnt;i++){
		if(cab[i] + c[cur] <= w){//剩余容量还够的话就尝试放入其中 
			cab[i] += c[cur];
			dfs(cur + 1,cnt);
			cab[i] -= c[cur];//恢复现场 
		}
	}
	
	cab[cnt + 1] += c[cur];
	dfs(cur + 1,cnt + 1);
	cab[cnt + 1] -= c[cur];//还原现场 
}

int main(){
	while(cin >> n >> w){
		memset(cab,0,sizeof(cab));
		ans = n;
		for(int i = 1;i <= n;i++)
		cin >> c[i];
		sort(c + 1, c + n + 1);
		reverse(c + 1, c + n + 1);
		dfs(1,0);
		cout << ans << endl;
	}
	return 0;
} 

　　上面两个优化(剪枝)技巧

1.搜索顺序是从大的猫开始，因为大的猫体积的，剩下的容量可放入的猫选择更少了。你的分支就少了

2.如果当前答案比已经得到的答案不优直接回溯，因为你再下去不会得到比已得到的答案更优

‘

下面看看数独吧，9*9

每一行每一列每个九宫格1~9的数字只出现一次

其实和我们模拟现实填数独是一样的

首先我们会选出可选数量最少的格子去填，那么这个格子所在的行和列以及九宫格的状态就变了

我们可以用包含九个二进制位来表示状态，然后搜索的时候就模拟吧

对于i，j这个位置所能选的是所在行列以及九宫格的交集那么把这三个的状态与就可以知道该位置可以添的数字是哪些

然后枚举直到枚举成功为止

#include<bits/stdc++.h>
using namespace std;

const int N = 9;

int row[N],col[N],ones[1 << N],mp[1 << N];
int cell[3][3];

char s[100];

inline int lowbit(int x){
	return x & -x;
}

void init(){
	for(int i = 0;i < (1 << N);i++){
		int cnt = 0;
		for(int j = i; j ; j -= lowbit(j))
		cnt++;
		ones[i] = cnt;
	}
	
	for(int i = 0;i < N;i++)
	mp[(1 << i)] = i;
}

inline int GetAns(int x,int y){
	return row[x] & col[y] & cell[x/3][y/3];
}

bool Dfs(int cur){
	if(!cur) return true;
	int minv = N + 1,x,y;
	
	for(int i = 0;i < N; i ++)//寻找最少决策数 
	for(int j = 0;j < N; j ++){
		int tc= i * N + j;
		if(s[tc] == '.'){
			if(ones[GetAns(i,j)] < minv){
				minv = ones[GetAns(i,j)];
				x = i;
				y = j;
			}
		}
	}
	
	for(int i = GetAns(x,y); i ; i -= lowbit(i)){
		int now = lowbit(i);
		int fa = mp[now];
		row[x] -= 1 << fa;
		col[y] -= 1 << fa;
		cell[x/3][y/3] -= 1 << fa;
		s[x*N + y] = '1' + fa;
		
		if(Dfs(cur - 1)) return true;
		
		row[x] += 1 << fa;
		col[y] += 1 << fa;
		cell[x/3][y/3] += 1 << fa;
		s[x*N + y] = '.';
	} 
	return false;
}

int main(){
	
	init();
	
	while(cin >> s , s[0] != 'e'){
		for(int i = 0;i < N;i++)
		{
			row[i] = (1 << N) - 1;
			col[i] = (1 << N) - 1;
		}
		
		for(int i = 0;i < 3;i++)
		for(int j = 0;j < 3;j++){
			cell[i][j] = (1 << N) - 1;
		}
		
		int tot = 0;
		for(int i = 0;i < 81; i ++){
			if(s[i] != '.'){
				int x = i/N,y = i % N;
				int tem =  s[i] - '1';
				row[x] -= 1 << tem;
				col[y] -= 1 << tem;
				cell[x/3][y/3] -= 1 <<  tem;
			}
			else tot++;
		}
		
		Dfs(tot);
		
		cout << s << endl;
	}
	return 0;
}