Computer Generated
Angular Fisheye Projections
Written by Paul Bourke
May 2001
There are two main idealised fisheye projections common in
computer graphics rendering, they are the hemispherical and
angular fisheye. They are two from an
infinite number of ways of mapping wide angle of view onto
an image plane.
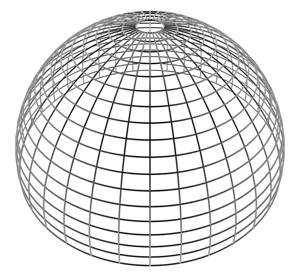
Hemispherical fisheye
A hemispherical fisheye, see figure 1, is a parallel projection of a
hemisphere onto a plane, the resulting image will be circular.
The widest view angle is 180 degrees (as shown) with extreme distortion
at +/- 90 degrees.
Because of the distortion introduced radially it is used less often than
the angular fisheye distortion.
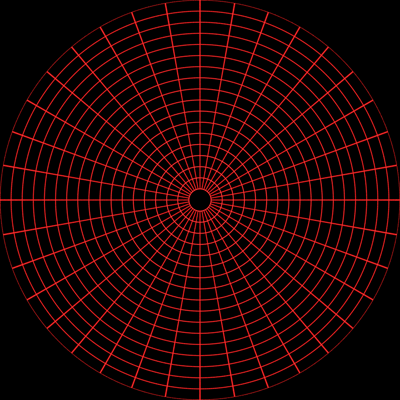
Angular fisheye
An angular fisheye projection is defined so that distance from the
center of the image is proportional to the angle from the camera
view direction. In particular, in an angular fisheye (also called f-theta lens)
image the resolution is approximately equal across the whole image.
An angular fisheye projection can be used for angles
all the way up to a full 360 degree. A cross section of a 360 degree
angular fisheye is shown in figure 2 and a 180 degree angular fisheye
in figure 3. The main point to note is that the distance from the
center of the image (a circle on the image plane) maps directly onto
the angle around the projection sphere.
A 180 degree fisheye projects half the environment onto a circular
image, a 360 degree fisheye projects the whole environment onto a
circular image. As an aside, while it is quite easy to get 180 degree
fish eye lens and even up to 220 degrees, it is also feasible to photograph
almost a 360 degree fisheye. This can be accomplished by photographing
a silvered ball using a telephoto lens. Note that the images captured with
real fisheye lens will have other distortions to the ideal lens described
here.
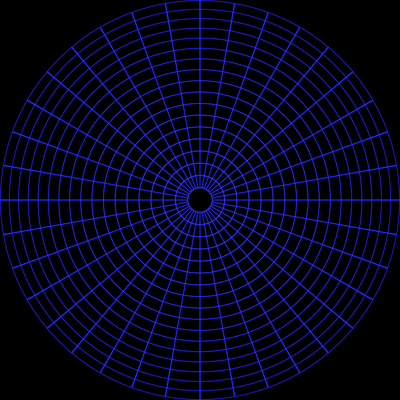
The image below is a 180 degree angular fish eye projection rendered
using the PovRay raytracer.
Creating an angular fisheye
To create an angular fisheye projection one needs to determine the
vector from the camera into the scene for every point in the image plane.
Figures 4 through 7 outline the procedure, at least, one possible
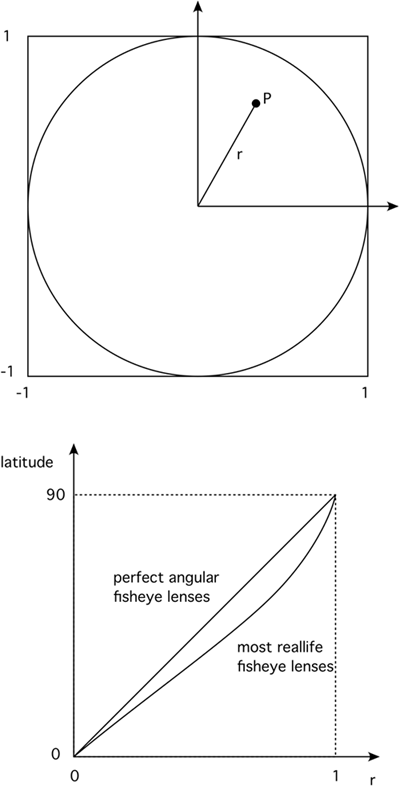
method. First the image coordinates are transformed from pixel
coordinates (i,j) into normalised coordinates (x,y) ranging from -1 to 1,
figure 5.
Next the radius r and angle phi to the x axis is calculated, figure 6. Note
that if atan2() is supported in your maths library then that can be
used as a more direct way of calculating the angle phi. At this stage
any pixels where r > 1 are ignored (drawn black or some other background
colour). Finally, r is mapped onto theta, phi is used directly as
the polar coordinates of the direction vector from the camera into the scene.
The angle theta is just r multiplied by half the intended fisheye angle
which may be anything up to 360 degrees.
Inverse transform
One way to use fisheye projections is as environment maps. In this case
one generally uses a 180 degree angular fisheye image and maps it onto
a hemisphere centered at the virtual camera. The general requirement
is to create the correct u,v texture coordinates for each vertex making
up the polygons on a unit radius hemisphere. Most texture mapping requires u,v
coordinates between 0 and 1 in each direction, the formula based upon
the conventions used here is as follows for a unit vector (x,y,z).
u = r cos(phi) + 0.5
v = r sin(phi) + 0.5
where
r = atan2(sqrt(x*x+y*y),p.z) / pi
phi = atan2(y,x)
There are many ways to create a polygonal representation of a unit
hemisphere. Two examples are given below in pseudo C code. The first
uses a grid in the x,y plane and calculates the z value using the
equation of the sphere x2 + y2 + z2 =
r2. The second creates a sphere using polar coordinates with
one pole directly in front of the camera. In both cases the sphere is
of unit radius and centered at the origin.
Method 1 - grid
Method 2 - polar
Note that for the above the normal at each point is the same
as the point itself. The value of N above relates to the resolution of the
sphere, the higher the more polygons created. In reality one might choose
more efficient methods than the above since it computes the same point
multiple times (for shared vertices). For example both methods can be
easily modified to support quad or triangle strips for OpenGL.
The texture coordinate for any point on the sphere
might be calculated as follows.
Source Code
Paraboloid
For completeness it should be mentioned that another way to record
wide angle views for environment maps is to use a paraboloid. The
main advantage is that there are efficient numerical methods for
unmapping the image for standard perspective views. Figure 8 shows
the cross section, the formula is generally something of the form.
z = 0.5 - 0.5 (x2 + y2)
for x2 + y2 <= 1
References
Max, N.,
Computer Graphics Distortion for IMAX and OMNIMAX Projection.
Proc Nicograph 83, Dec 1983 pp 137.
Greene, N.,
Environment Mapping and Other Applications of World Projections
IEEE Computer Graphics and Applications, November 1986, vol 6, no 11, pp 21
Wyvill, G., McNaughton, C.,
Optical Models
Computer Graphics International, 1990, Springer p88
Fleck M.,
Perspective projection: The wrong imaging model
University of Iowa, Tech Report #95-01
Svoboda, T., Pajdla, T., Hlavac, V.,
Central Panoramic Cameras: Geometry and Design
Czech Technical University, Tech Report K335/97/147.
|
Figure 1
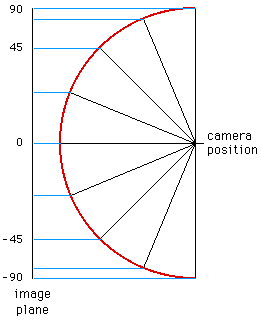
Figure 2
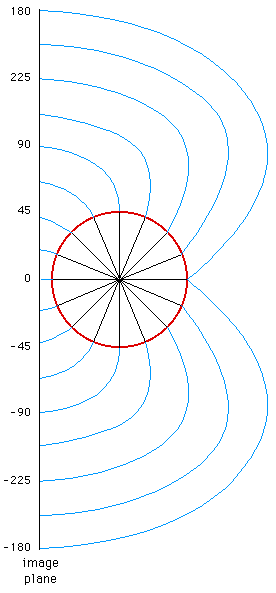
Figure 3
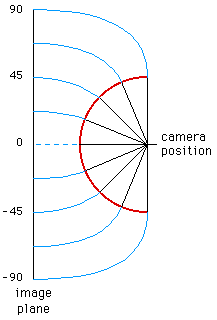
Figure 4
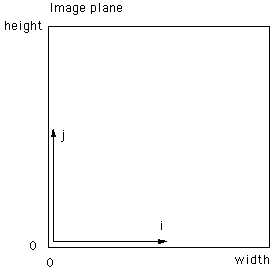
Figure 5
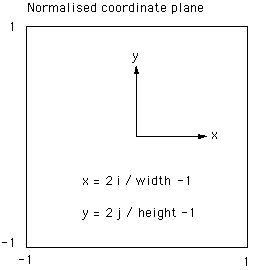
Figure 6
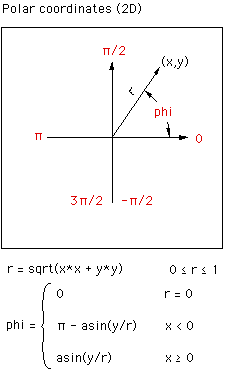
Figure 7
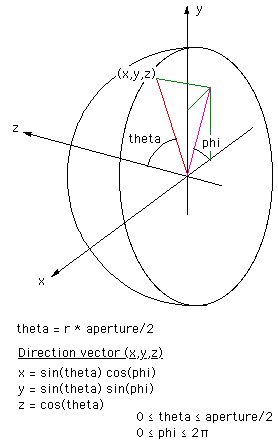
Figure 8
|
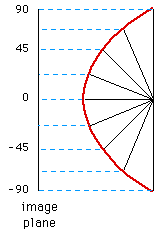
Non linearily
Real fisheye lenses rarely follow the precise linear relationship between radius
on the fisheye image plane and latitude. The most common form of deviation is a compression of the
image towards the rim of the fisheye circle.
Of course if this non-linearity is a problem it can be corrected for, at the
expense of some loss of resolution at the rim.
Appendix: Approximations
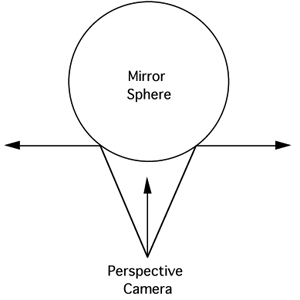
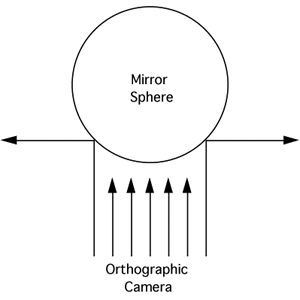
Some raytracing packages don't support a native fisheye camera, the question
is often asked "can a spherical mirror be used to create a fisheye view?".
The basic idea is to render the view of the scene by pointing the virtual
camera at a perfectly reflective spherical surface. The answer is "the
result is close but not exactly correct". Three rendering are shown below,
the scene is simply a hemisphere represented as a regular grid of lines
of latitude and longitude.
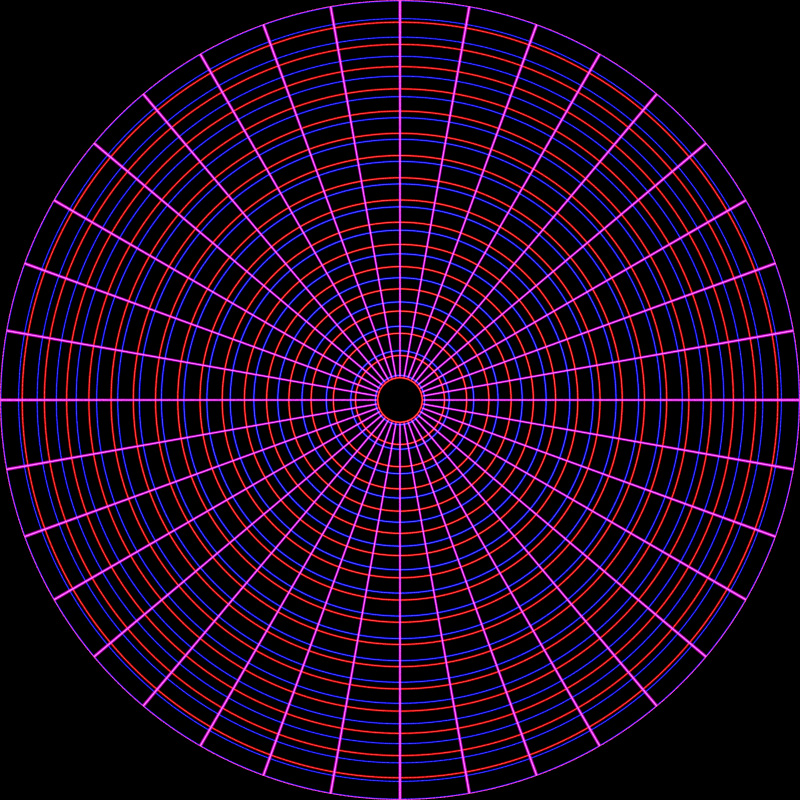
Overlap of fisheye and orthographic mirror
The following is the perfect fisheye superimposed with the orthographic
rendering. The biggest difference is around the mid latitudes, for example,
if such a projection was used in a planetarium then objects that remain at the
same distance from the camera but move from the pole to the horizon will
appear to change size.
It should be noted that a mirror (not spherical) can be designed such
the correct result is achieved. In the authors opinion it is vastly better
to render cubic maps from which correct fisheye projections can be derived.
Offaxis fisheye projection
Written by Paul Bourke
October 2001, modified January 2004
Introduction
There exist a number of full dome environments that project angular fisheye
or other radial functions. If the angular fisheye is created correctly then
the resulting image after projection onto the dome surface appears
undistorted. Unfortunately if the projector uses a single fisheye lens
then the standard fisheye projection as described
here requires that both the lens and the
viewer are located at the center of the dome, obviously impossible.
As the viewer moves away from the center the image appears increasingly
distorted. This isn't normally a problem for large planetariums
where the radius of the dome is very much larger than the seating area and
in any case nothing can be done since there are multiple viewers.
For smaller domes the effect is more marked and the viewer can easily
move significant distances from the center. It is possible to create
a modified fisheye image so that if viewed from a particular position
the projected image will appear undistorted, this is called an off axis
fisheye image. This is the same principle employed when creating stereo
pairs where one uses an off-axis (asymmetric) perspective frustum for
each eye.
Algorithm
|
Creating an off-axis fisheye is quite straightforward. First, create the
fisheye projection world vector
p as described here.
The vector
p' is derived as shown in the diagram on the right.
The new ray p' is the ray
p minus the vector to the
view position.
While the diagram on the right shows the view position
along the y axis, it is normally
applied to any point in the x,y plane as the dome viewer
will most commonly move around on that plane.
Note that as the viewer moves towards the rim the image gets increasingly
stretched in that direction. This violates the usual characteristic of angular
fisheye images where a pixel in image space is proportional to the angle in
fisheye space. Or put another way, all pixels in the fisheye image are
the same dimensions in the projected image, this can be seen in the example
below.
Viewer at (0,0)
|
Viewer at (0.5,0.5)
|
|
|
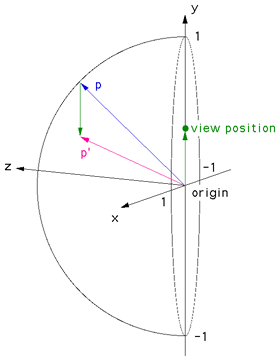
Figure 1
|
A common approach to creating content for dome environments is to
render standard projections onto the faces of a cube. The off-axis
fisheye can be computed from these at interactive rates and so a
single viewer with a head tracking device can be presented with
a corrected image as they walk around the base of the dome.
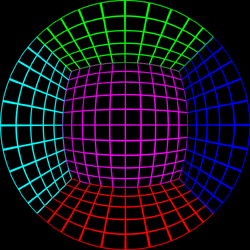
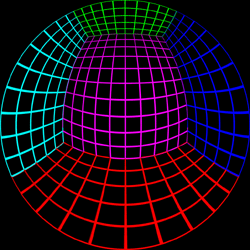
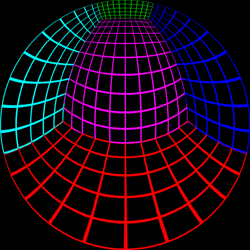
Test Pattern
The following test pattern was used to test the correctness of the
off-axis fisheye. It is a rendering of a
cubic room, each wall is a
different colour and constructed with a regular grid of bars. If
the fisheye generation is correct the curved lines in the fisheye
image should appear straight when projected onto the dome. The
coordinate above each image is the position of the viewer.
Offset = (0,0)
 |
Offset = (0,0.5)
 |
Offset = (0,0.75)
 |
Offset = (0,0.95)
 |
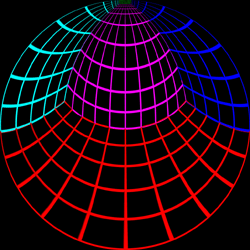Offset = (0.5,0.5)
 |
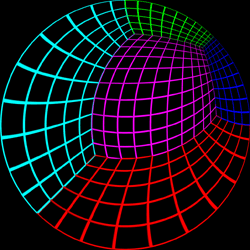Offset = (0.7,0.7)
 |
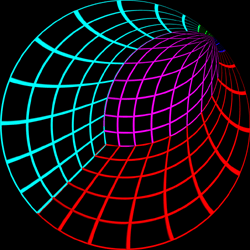This example is rendered in PovRay onto a
5 wall cubic environment map, the off-axis fisheye
is created from these 5 images.
(5view.ini,
5view.pov,
5viewcamera.pov)
This has the advantage of being
able to create multiple offaxis fisheye images from one set of
cubic environment maps, this would not be possible if the offaxis
fisheye was rendered directly in PovRay (something that is easy to
arrange by modifying the PovRay source code).
Creating offaxis projections from existing fisheye images
Given an existing fisheye image, an offaxis fisheye can be created
for any offaxis position. There is a full mapping for 180 degree
fisheye images, smaller angle images result in an incomplete
mapping.
It reads a TGA image representing a fisheye image and creates
an offaxis fisheye as another TGA file. Note that there are
important resolution issues to consider, this works best when
going from very high resolution fisheye images to lower
resolution ones. The code here is a simple command line
based UNIX utility, it supports supersampling antialiasing
and variable output image size.
offaxis tgafilename [options]
Options:
-a n set antialias level (Default: 1)
-w n width of the output image (Default: 500)
-h n height of the output image (Default: width)
-dx n x component of the offaxis vector (Default: 0)
-dy n y component of the offaxis vector (Default: 0)
-v debug/verbose mode (Default: off)
Original fisheye image
|
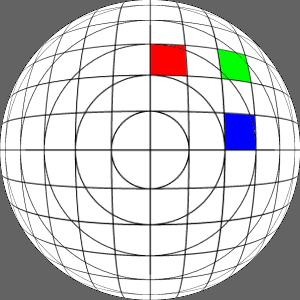
X axis offset of 0.3
|
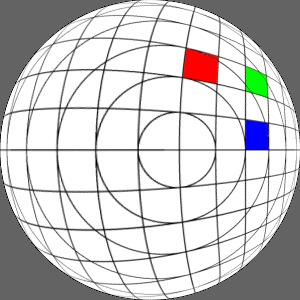
Y axis offset of 0.3
|
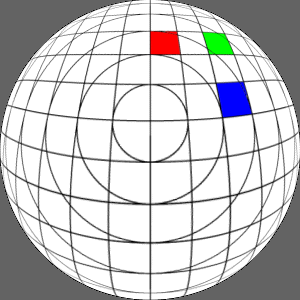
X and Y axis offset of 0.3
|
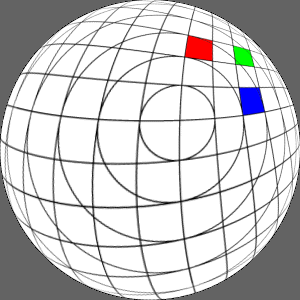
Photos of a Prototype Dome
Example Images used in the Prototype Dome
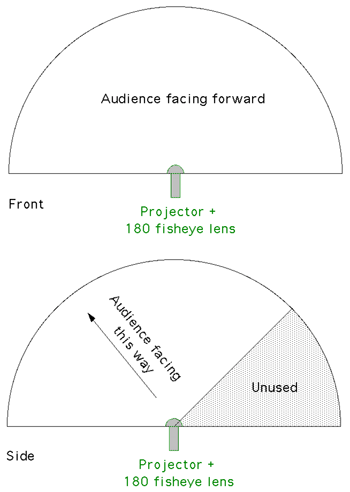
Note that for these tests an Elumens projector was used. This is a
standard projector with their fisheye lens and as such the projector
projects a 4:3 width to height ratio while fisheye images are 1:1.
This is addressed by clipping off 25% of the image, in the case of the
Elumens dome this is normally the bottom 25%. In our case we chose to
clip the top 25%, this conveniently gave the viewers a position behind
the projector from which to view the images without being blinded.
|
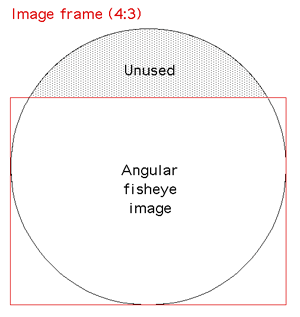Figure 2
|
Addendum
The offaxis correction as described above only applied to shifting the
observer around on the rim plane of the hemisphere. A similar correction
can be made to compensate for the observer being within the dome, or in
the more likely case, away from the rim of the dome (along the negative z axis,
see figure 1). This correction is
applied in exactly the same way but note that it results in a reduced
field of view unlike offset positions on the rim plane which result in
stretching distortion but the same field of view.
网址：
http://paulbourke.net/dome/fisheye/
|
