1.学习总结
1.1树结构思维导图
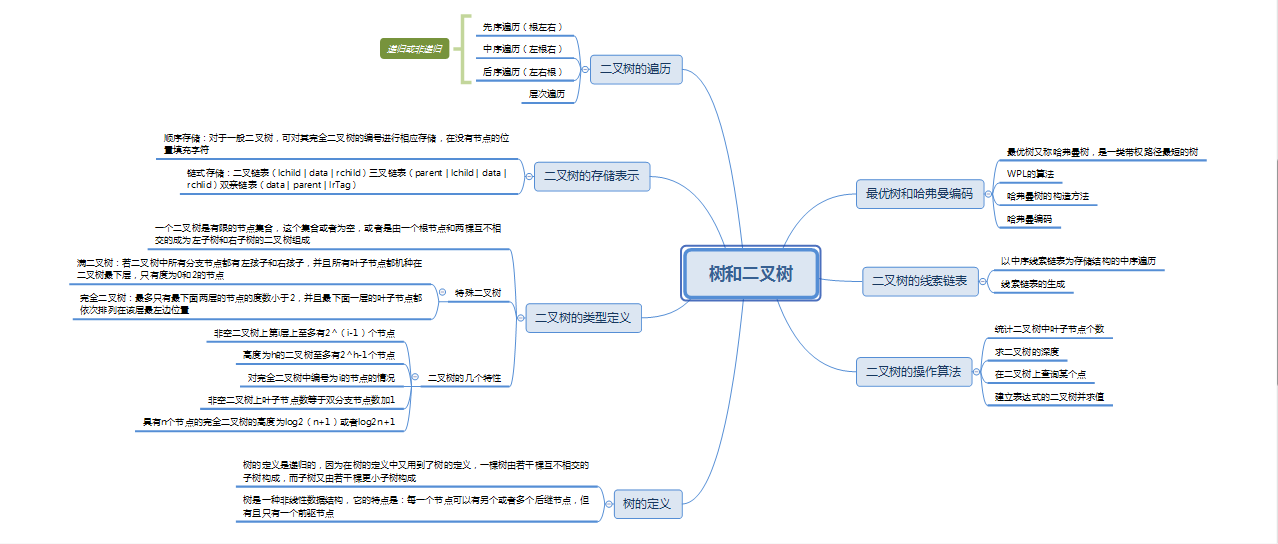
1.2 树结构学习体会
- 感觉树的内容很难,一些逻辑比较难弄懂,而且内容比较多,所以还是得花时间去理解,树不比先前的那些线性结构,多了很多新东西,比如带权路径长度,哈弗曼编码什么的,总之要学起来真的不容易。
2.PTA实验作业
1.题目1:6-2 求二叉树高度
1.1设计思路(伪代码或流程图)
int GetHeight( BinTree BT )
{
定义LD,RD分别表示左子树高度和右子树高度
如果BT==NULL 返回0
否则递归调用该节点的左节点和右节点(后序遍历)
最后返回max{LD,RD}+1
}
1.2代码截图

1.3PTA提交列表说明

- 此题在编译器上出现的错误:LD和RD的最大值没有加一再返回,导致答案错误;
2.题目1:6-4 jmu-ds-表达式树
2.1设计思路(伪代码或流程图)
void InitExpTree(BTree &T,string str)
{
建立op栈存运算符
op.push('#')
初始化根节点栈stacktree栈
while(str[i])
{
如果str[i]是操作数
生成一个只有根节点的子树T,stacktree.push(T)
如果str[i]是运算符{
switch(栈顶元素与str[i]的优先级)
大于:创建一个树节点T,数据为op.top
stacktree弹出两个节点T1,T2
T->lchild=T1,T->rlchild=T2
stacktree.push(T)
小于:op.push(str[i])
等于:op.pop()
}
}
while(op.top()!='#'){
创建一个树节点T,数据为op.top
stacktree弹出两个节点T1,T2
T->lchild=T1,T->rlchild=T2
stacktree.push(T)
op.pop()
}
T=stacktree.top()
}
double EvaluateExTree(BTree T)
{
定义变量a,b
递归出口:(!T->lchild&&!T->rchild)
返回T->data-'0'
递归调用左右节点
a=EvaluateExTree(T->lchild)
b=EvaluateExTree(T->rchild)
判断操作符
进行相应计算
}
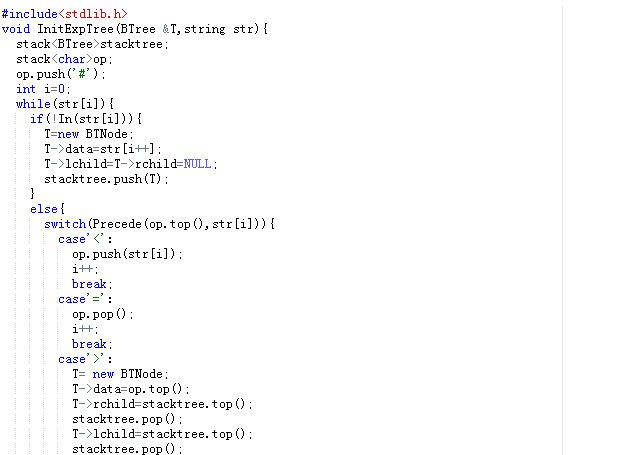
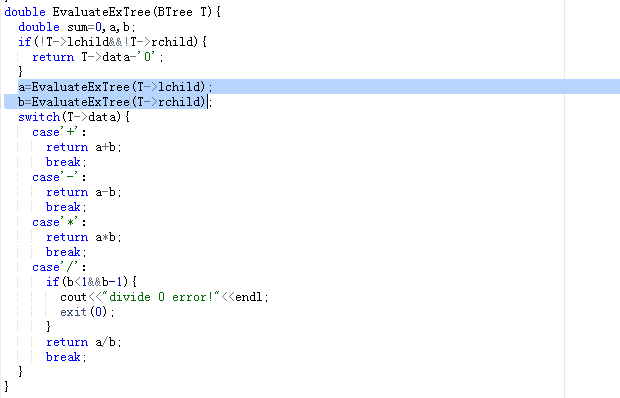
2.2代码截图

2.3PTA提交列表说明
- 此题频繁出现段错误,至今不知道是什么原因。后面参考了其他同学的代码,发现自己在建表达式树的时候,忽略了op栈中不空的时候,还是要继续出栈,因此在后面加一个while循环,表达式树的代码一开始把它复杂化了,想到的是还是利用栈对树进行遍历求值,类似于后缀表达式求值,后面看到其他同学的代码使用递归法求的,感觉简洁了很多,但是还是不太能理解
3.题目1:7-8 jmu-ds-二叉树叶子结点带权路径长度和
3.1设计思路(伪代码或流程图)
BTree CreateBtree(string str,int i)//递归法建树
{
递归出口:
(i>str.size()-1)或者(str[i]=='#')
BTree b;
申请空间,初始化将字符转为整型
b->lchild=CreateBtree(str,2*i);
b->rchild=CreateBtree(str,2*i+1);
}
定义一个全局变量count
void WPL(BTree b,int n)
{
if(b!=NULL){
如果是叶节点 count=count+b->data*n
否则 继续调用左右节点
WPL(b->lchild,n+1)
WPL(b->rchild,n+1)
}
}
3.2代码截图
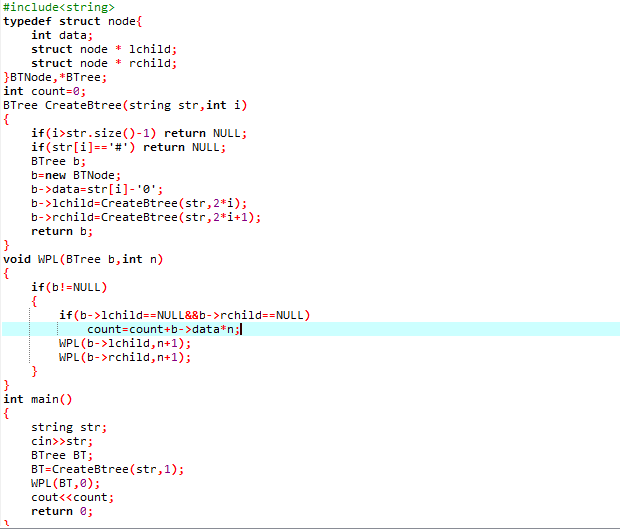
3.3PTA提交列表说明

- 在调用建树函数时应该是从1开始,第一个井号不算,一开始从零开始,导致只有空树时正确
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的得分:2分
PTA总分:205 在180-230之间
4. 阅读代码
二叉排序树插入代码
void Insert_BST(BST_P *root, DataType data)
{
BST_P p = (BST_P)malloc(sizeof(struct BST_Node));
if (!p) return;
p->data = data;
p->lchild = p->rchild = NULL;
if (*root == NULL)
{
*root = p;
return;
}
if (Search_BST(root, data) != NULL) return;
BST_P tnode = NULL, troot = *root;
while (troot)
{
tnode = troot;
troot = (data < troot->data) ? troot->lchild : troot->rchild;
}
if (data < tnode->data)
tnode->lchild = p;
else
tnode->rchild = p;
}
- 首先初始化插入节点,空树时,直接作为根节点,然后进行查找,看是否存在,如果已存在则返回,不插入,在进行出入的时候,要先找到插入位置的父节点,然后在判断插在左子树还是又子树。这段代码的有点在于逻辑很清晰,而且很简洁,各种情况都考虑到位,特别是查找插入位置的父节点时,用了troot = (data < troot->data) ? troot->lchild : troot->rchild;这个语句,简洁易懂。然后我在思考有没有递归的方法。
5. 代码Git提交记录截图