动态规划-背包问题

// 最优原则：不管前面的策略如何，此后的决策是是基于当前状态（由上一次决策产生）的最优决策。
// 当最优决策序列中包含最优决策子序列时，可建立动态规划递归方法。
// （有些问题的递归式不一定能保证最优原则，因此在求解时有必要对它进行验证。若不能保持最优原则，则不可应用动态规划方法。）
// 在得到最优解的递归式之后，需要执行回溯以构造最优解。
// 缺点：如果不努力地去避免重复计算，递归程序的复杂性将非常可观。
// 方案：如果在递归程序中解决了重复计算问题时，复杂性将急剧下降。
// 递归方程也可用迭代方程来求解，这很自然地避免了重复计算。迭代方程虽然具有相同的复杂性，不需要附加的递归栈空间，因此更快一些。

参考博客：

1、动态规划之01背包问题（最易理解的讲解）

2、0-1背包问题--动态规划算法

3、背包问题  递归方法

问题描述：
 　　给定n种物品和一背包，物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品（物品不能分割），使得装入背包中物品的总价值最大?

分析：

　　设f(i,j)为装入背包中的最大总价值，其中i是前i个物品，j是指背包剩余的承重,不是总承重。

　　1、把这个问题抽象成找到最优数组问题，x[0],x[1],x[2],x[3].....是一个01序列，其中1表示装入，0表示不装入。

　　2、假设当前状态找到的最优解序列是x[0],x[1],x[2],x[3]...x[j]，能使总价值最大。

　　　  对于第j个物品是否装入，需要进行比较

　　　　　　1)当w[j]>load,当这个物品的重量大于包剩余承重时，则无法装入，此时最大总价值等于前i-1个的最大总价值

　　　　　　　　　　　　   则  f(i,j)=f(i-1,j)

　　　　　　2)当w[j]<=load时，

　　　　　　　　　　则需要比较两个值，f(i,j)=max{f(i-1,j-w[i])+v[i] , f(i-1,j)}

　　　　　　　　  假如要装入第i个物品的话，则需要花掉w[i]的承重，则对于前i-1个物品来说，总价值是f(i-1,j-w[i])+v[i]。

　　　　　　　　  假如不装入的话，总价值是f(i-1,j)。

　　　　　　　　  取两者的较大值。

　　　上面的每个式子都包含了子序列，可以采用动态规划的方法解。

 

　　　******下面是另外一种顺序。

         

         

 

 

　　　　*******

  　 3、采用递归和非递归方式解答。

 

程序（非递归）：

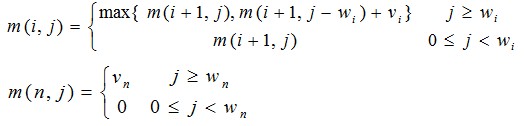
有编号分别为a,b,c,d,e的五件物品，它们的重量分别是6,4,3,5,7，它们的价值分别是3,7,6,6,5，现在给你个承重为10的背包，如何让背包里装入的物品具有最大的价值总和？

采用填表法

名称	weight	value	0	1	2	3	4	5	6	7	8	9	10
a	6	3	0	0	0	0	0	0	3	3	3	3	3
b	4	7	0	0	0	0	7	7	7	7	7	7	10
c	3	6	0	0	0	6	7	7	7	13	13	13	13
d	5	6	0	0	0	6	7	7	7	13	13	13	13
e	7	5	0	0	0	6	7	7	7	13	13	13	13

只要你能通过找规律手工填写出上面这张表就算理解了01背包的动态规划算法。

首先要明确这张表是从上往下，从左到右生成的。(****这里和参考的那篇文章正好相反)

 这张表的填写的规律：

　　1、先填写第0行的数据   if(load>w[i])  f(0,j)=v[i]    else  f(0,j)=0;

　　2、从上往下依次填写，f(i,j)=max{f(i-1,j-w[i])+v[i]  ,  f(i-1,j)}

　　　  比如c10  (第c行第10列)  f(2,10)=  max {f(1,10)    ,   f(1,10-6)+6}  ->  max{10  ,  7+6}  =  13 。

　　3、最大总价值自然就是   f(n-1,c)。

    public static void main(String[] args) {
        int[] weights={6,4,3,5,7};
        int[] values={3,7,6,6,5};
        boolean [] selected=new boolean[weights.length];
        System.out.println(getMaxReverse(weights, values, weights.length, 10));
        System.out.println(getMax(selected, weights, values, 1, 10));
        System.out.println(getMax(weights, values, 10));
    }
    /**
     * 背包问题第一步：获得动态公式
     * f(i,j)=Max{f(i-1,j-Mi)+Pi,f(i-1,j)}
     * f(i,j)表示前i件物品放在承重j的背包中的最大价值
     * Mi是第i件物品的重量，Pi是第i件物品的价值
     */
    public static int getMaxReverse(int [] weights,int[] values,int index,int load)
    {
        if(index==0 || load==0) return 0;
        if(weights[index-1]>load)//不选择当前
        {
            return getMaxReverse(weights, values, index-1, load);
        }
        else
        {
            //选择当前
            int m1=getMaxReverse(weights, values, index-1, load-weights[index-1])+values[index-1];
            //不选择当前
            int m2=getMaxReverse(weights, values, index-1, load);
            return Math.max(m1, m2);
        }
    }
    
　　//在递归里面确定装了哪些物品不靠谱
    public static int getMax(boolean[] selected,int [] weights,int[] values,int index,int load)
    {
        if(index==weights.length) return weights[index-1]>load?0:values[index-1];
        if(weights[index-1]>load)
        {
            selected[index-1]=false;
            return getMax(selected, weights, values, index+1, load);
        }
        else {
            int v1=getMax(selected, weights, values, index+1, load);
            int v2=getMax(selected, weights, values, index+1, load-weights[index-1])+values[index-1];
            if(v1>v2)
            {
                selected[index-1]=false;
                return v1;
            }
            else 
            {
                selected[index-1]=true;
                return v2;
            }
        }
    }
    /**
　　　　非递归解法
　　*/
    public static int getMax(int [] weights,int[] values,int load)
    {
        //新建数组用于存放数据
        //load+1的作用是取索引方便
        int len=weights.length;
        int[][] maxSum=new int[len][load+1];
        //第一步初始化第0行
        for(int i=0;i<load+1;i++)
        {
            maxSum[0][i]=weights[0]>i?0:values[0];
        }
        //从第1行到第n-1行
        for(int i=1;i<len;i++)
        {
            for(int j=0;j<load+1;j++)
            {
                if(j>=weights[i])
                    maxSum[i][j]=Math.max(maxSum[i-1][j], maxSum[i-1][j-weights[i]]+values[i]);
                else 
                    maxSum[i][j]=maxSum[i-1][j];
            }
        }
        for(int i=0;i<len;i++)
            System.out.println(Arrays.toString(maxSum[i]));
        //输出选择的物品
        int temp=load;
        for(int i=len-1;i>0;i--)
        {
            if(maxSum[i][temp]!=maxSum[i-1][temp])
            {
                System.out.println("取了第"+(i+1)+"件物品 重量"+weights[i]+"  价值"+values[i]);
                temp-=weights[i];
            }
        }
        //返回
        return maxSum[len-1][load];
    }