59.螺旋矩阵二

题目描述：

 给定一个正整数 n，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

 示例:

 输入: 3
 输出:
 [
   [ 1, 2, 3 ],
   [ 8, 9, 4 ],
   [ 7, 6, 5 ]
 ]

题解：

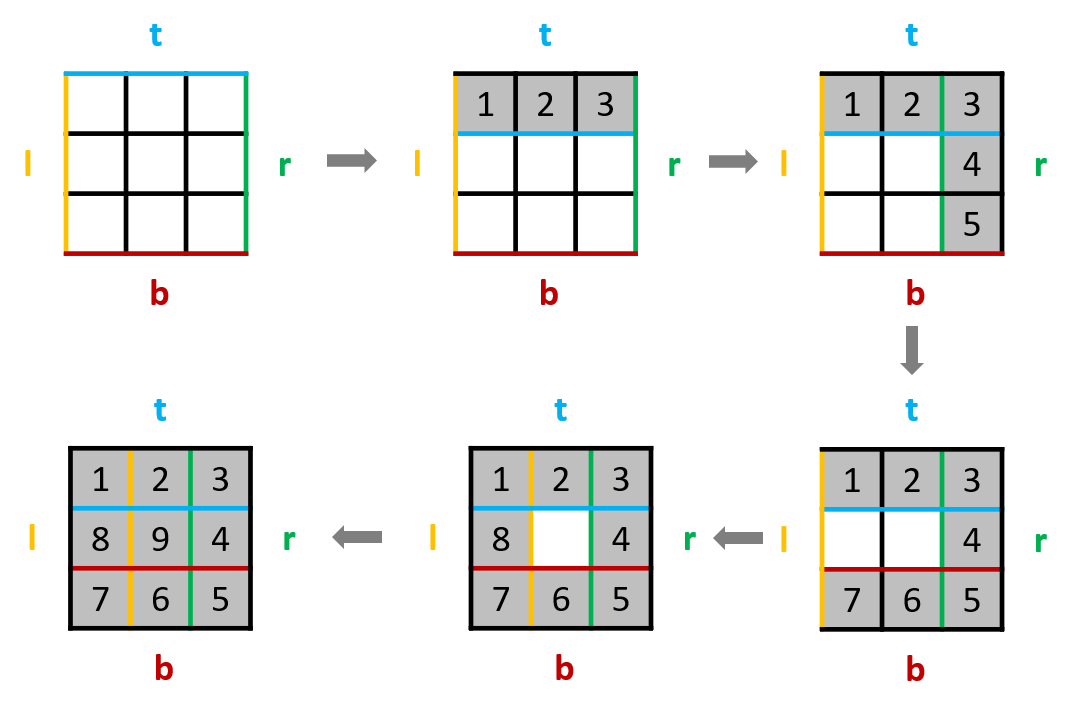
生成一个 n×n 空矩阵 mat，随后模拟整个向内环绕的填入过程：
定义当前左右上下边界 l,r,t,b，初始值 num = 1，迭代终止值 tar = n * n；
当 num <= tar 时，始终按照 从左到右 从上到下 从右到左 从下到上 填入顺序循环，每次填入后：
执行 num += 1：得到下一个需要填入的数字；
更新边界：例如从左到右填完后，上边界 t += 1，相当于上边界向内缩 1。
使用num <= tar而不是l < r || t < b作为迭代条件，是为了解决当n为奇数时，矩阵中心数字无法在迭代过程中被填充的问题。
最终返回 mat 即可。

public class L59 {
    public static int[][] generateMatrix(int n) {
        int[][] re = new int[n][n];
        int l = 0,t = 0,r = n ,b = n;
        int index = 1;
        while(index <= n *n){
            for(int i = l;i<r;i++){
                re[t][i] = index ++;
            }
            t ++;
            for(int i = t;i<b;i++){
                re[i][r-1] = index ++;
            }
            r --;
            for ( int i = r-1;i >= l;i--){
                re[b-1][i] = index ++;
            }
            b --;
            for(int i = b-1;i>=t;i--){
                re[i][l] = index ++;
            }
            l ++;
        }
        return re;
    }

    public static void main(String[] args) {
        int[][] re = generateMatrix(3);
        int s = 0;
    }
}