5.6 向量化 Vectorization
参考视频: 5 - 6 - Vectorization (14 min).mkv
下面是向量化的小例子,如果将所有u(j) 、所有v(j)、所有w(j)都看成列向量,则公式变为为向量加法 u = 2v + 5w
![]()
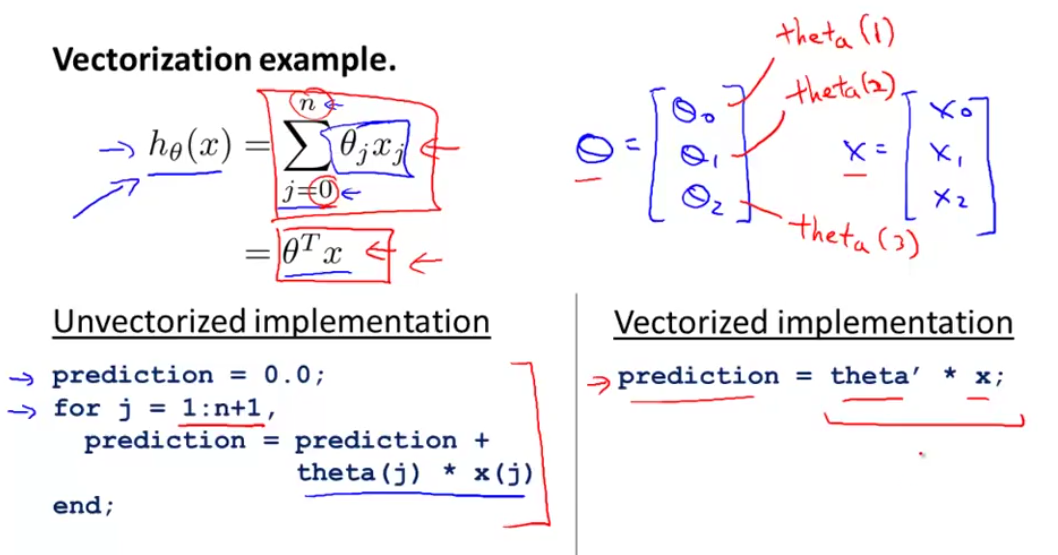
再复杂一些,在线性回归中 h(x) 的公式如下:

假设此时n=2,只有两个特征。将其向量化:
在Octave中,如果使用for循环实现,则为左边的代码。使用看做向量相乘,则只需要右边一行代码:
在C++中,for循环和向量化方法的对比如下:

当 n = 2 时,梯度下降的公式如下:

实现这三个方程的方式之一,是用一个 for 循环,让 j 分别等于 0、1、2 来更新 Θj。
因为三个参数是同步更新,可以用向量化的方法来实现。我们使用 δ 替代公式中下面这项(注意最右边 x 没有下标):

则δ是一个 n+1 维向量(在这里是3维)

α 是一个实数,α δ 也是 n+1 维向量
x(i) 是一个 n+1 维向量(在这里是3维)

公式变为一个向量减法:
Θ := Θ - α δ
有时我们使用几十或几百个特征量来计算线性归回,当使用向量化地实现线性回归,通常运行速度就会比 for 循环快的多