Codeforces Round #360 E

The Values You Can Make

题意：给n个数，第一次在这n个数中选出一些子序列，使得子序列和为k，然后再从这些和为k的子序列为k的数中再选出一些子序列，求第二次选出来的这些子序列的和的可能的值为多少，并升序输出（可以一个都不选）

思路：二维01背包方案数+滚动数组优化。

　　dp[i][j][k]表示当前有i个数，从这些数中选出和为j的子序列再选出和为k的子序列的方案数，若方案数不为0，说明可行

　　递推式为            

　　　　　　　　　

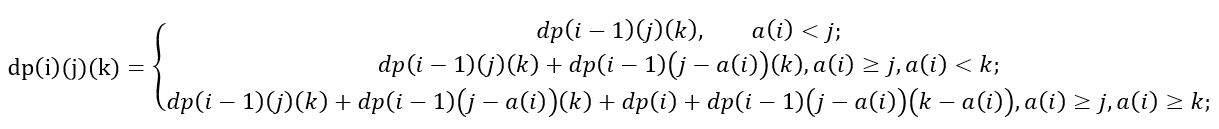
这里给的是逆推的公式（即第i个状态是由哪些状态转移过来的）因为比较好写公式，但是代码中给出的是正推（即当前状态可以转移成哪些状态），最后滚动数组优化空间

AC代码：

#include "iostream"
#include "string.h"
#include "stack"
#include "queue"
#include "string"
#include "vector"
#include "set"
#include "map"
#include "algorithm"
#include "stdio.h"
#include "math.h"
#pragma comment(linker, "/STACK:102400000,102400000")
#define ll long long
#define bug(x) cout<<x<<" "<<"UUUUU"<<endl;
#define mem(a,x) memset(a,x,sizeof(a))
#define mp(x,y) make_pair(x,y)
#define pb(x) push_back(x)
#define lrt (rt<<1)
#define rrt (rt<<1|1)
using namespace std;
const long long INF = 1e18+1LL;
const int inf = 1e9+1e8;
const int N=1e5+100;
const ll mod=1e9+7;

///EEEE
///设dp[i][j][k]表示前面i个数能构成的子序和为j的子序列能构造出子序和为k的数子序列。

int n,g,a[505],vis[505];
bool dp[3][505][505];
int ans[N];
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>g;
    for(int i=1; i<=n; ++i){
        cin>>a[i];
    }
    dp[0][0][0] = 1;
    bool cur=0;
    for(int i=0; i<n; ++i){
        for(int j=0; j<=g; ++j){
            for(int k=0; k<=j; ++k){
                if(j+a[i+1] <= g) dp[cur^1][j+a[i+1]][k] |= dp[cur][j][k];
                if(k+a[i+1] <= g) dp[cur^1][j+a[i+1]][k+a[i+1]] |= dp[cur][j][k];
                dp[cur^1][j][k] |= dp[cur][j][k];
            }
        }
        cur^=1;
    }
    int l=0;
    for(int k=0; k<=g; ++k){
        if(dp[cur][g][k] && !vis[k]){
            ans[++l]=k;
            vis[k]=1;
        }
    }
    sort(ans+1,ans+1+l);
    cout<<l<<endl;
    for(int i=1; i<=l; ++i) cout<<ans[i]<<" ";
    return 0;
}