(清华THUSSAT,多选题)
平面上 4 个不同点 (P_1,P_2,P_3,P_4),在每两个点之间连接线段得到 6 条线段. 记
对任意三点不共线的所有四点组 (P_1,P_2,P_3,P_4),把 (dfrac{L}{l}) 的取值集合记为 (P),则
A.(0.5 in P)
B.(1 in P)
C.(sqrt{2} in P)
D.(2 in P)

答案:C.D,构造如下:
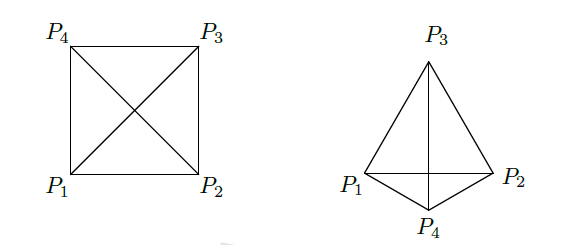
此题是著名的"Heilbronn问题"在4个点时的情形,一般的由以下结论(lambda_nge2cosdfrac{pi}{n})当(nge6)时尚不知道能否取到等号.
事实上1985全国联赛最后一题就是考察了5个点的情形.
(1985联赛加试)平面上任给5个点,以(lambda)表示这些点间最大的距离与最小的距离之比,证明:(lambda≥2sin54^o)
证明:
⑴ 若此五点中有三点共线,例如A、B、C三点共线,不妨设B在A、C之间,则AB与BC必有一较大者.不妨设AB≥BC.则(dfrac{AC}{BC}≥2>2sin54^o)

⑵ 设此五点中无三点共线的情况.
① 若此五点的凸包为正五边形.则其五个内角都(=108^o)五点的连线只有两种长度:正五边形的边长与对角线,而此对角线与边长之比为(2sin54^o).
② 若此五点的凸包为凸五边形.则其五个内角中至少有一个内角(≥108^o).设(angle EAB≥108^o),且(EA≥AB),则(angle AEB≤36^o, herefore dfrac{BE}{AB} = dfrac{sin(B+E)}{sinE} ≥dfrac{sin2E}{sinE} =2cosE≥2cos36^o=2sin54^o).
③ 若此五点的凸包为凸四边形ABCD,点E在其内部,连AC,设点E在(Delta ABC)内部,则(angle AEB,angle BEC,angle CEA)中至少有一个角(≥120^o>108^o),由上证可知,结论成立.
④ 若此五点的凸包为三角形ABC,则形内有两点D、E,则(angle ADB,angle BDC,angle CDA)中必有一个角(≥120^o),结论成立.
综上可知,结论成立.