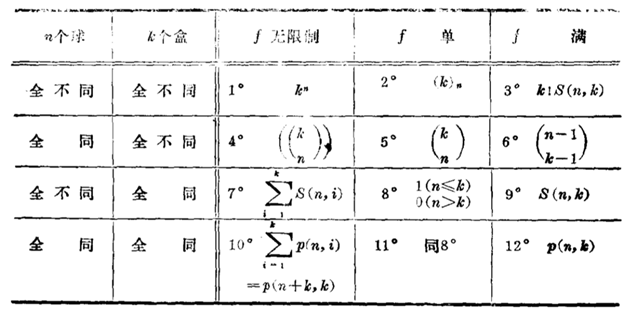
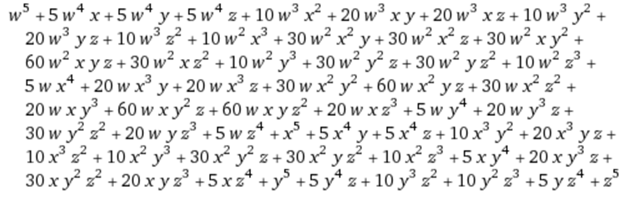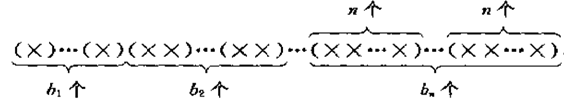先拿MT【100】的图表镇楼。
举几个例子:
【1】52张纸牌分发给4人,每人13张,问每人手中有一张小2的概率?
分析:第一步每人分一张小2,有4!种,然后48张牌平均分成4组有$frac{48!}{12!12!12!12!}$易得概率为$4!frac{48!(13!)^4}{52!(12!)^4}$大概为10.55%,有兴趣也可以算一下四张2都在某个人手里的概率。
【2】$(x+y+z+w)^5$的展开式有多少项?
分析:每一项都是5次方,相当于5个无区别的小球放入4个有标志的盒子里.每个盒子里放的球不加限制。也就是上表中第4种情况,有56种。$(x+y+z+w)^5$展开式如下:
注:顺便讲一下$x^2y^2z^1w^0$前的系数计算公式为$frac{5!}{2!2!1!0!}$可以类比二项式定理$(x+y)^5$展开中$x^2y^3$前的系数公式$frac{5!}{2!3!}$。
【3】$x_1+x_2+cdots+x_kle n$的非负整数解的个数.
分析:定义如下映射$(x_1,x_2,cdots,x_k)mapsto (x_1+1,x_1+x_2+1,cdots,x_1+cdots+x_k+k)$是$x_1+x_2+cdots+x_kle n$的非负整数解集到${1,2,cdots,n+k}$中取$k$项严格单调递增数列集合的一个一一映射,有$dbinom{k+n}{k}$
注:这里可以得到一个恒等式:$sum_{i=0}^{n}dbinom{k+i-1}{i}=dbinom{k+n}{n}$
【4】已知$b_1+2b_2+cdots+nb_n=n$其中$b_1,b_2,cdots,b_nin N$,把${1,2,cdots,n}$的一个全排列放入以下框架中
问有多少种不同形式.
答:$frac{n!}{b_1!b_2!cdots b_n!1^{b_1}2^{b_2}cdots n^{b_n}}$即对称群$S_n$中$1^{b_1}2^{b_2}cdots n^{b_n}$型的元素个数。