已知$ heta in[0,2pi]$求$2cos heta-sin heta-dfrac{sin heta+sqrt{5}}{cos heta+sqrt{5}}$的最小值_____
分析:$2cos heta-sin heta-dfrac{sin heta+sqrt{5}}{cos heta+sqrt{5}}= extbf{ON}cdot extbf{OP}+k_{PM}ge-sqrt{5}-2$
当$P(-dfrac{2}{sqrt{5}},dfrac{1}{sqrt{5}})$时取到最小值.
如图$M(-sqrt{5},-sqrt{5}),N(2,-1)$

注:最大值可以用万能公式变形为
$2cos heta-sin heta-dfrac{sin heta+sqrt{5}}{cos heta+sqrt{5}}=dfrac{2-2t^2-2t}{1+t^2}-dfrac{sqrt{5}t^2+2t+sqrt{5}}{(sqrt{5}-1)t^2+1+sqrt{5}}$
其中$t= andfrac{ heta}{2}in R$求导可知
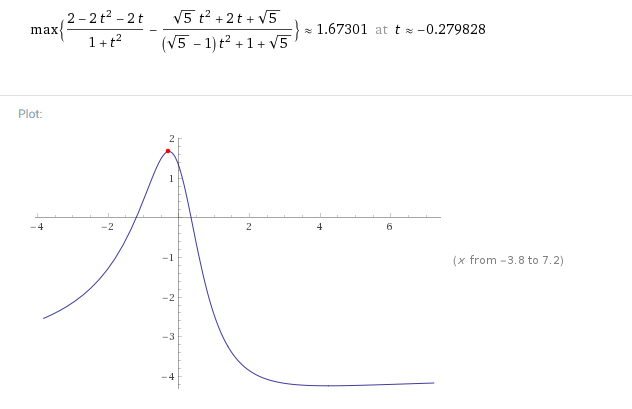
最小值几何意义明显,适合做考题.最大值不适合做考题