若$Delta ABC$满足:$ andfrac{A}{2}cdot andfrac{C}{2}=dfrac{1}{3},b=dfrac{4}{3}a$,则$sin B=$______

分析:$ andfrac{A}{2}cdot andfrac{C}{2}=dfrac{1-cos A}{sin A}cdotdfrac{sin C}{1+cos C}=dfrac{1}{3}$
得 $dfrac{a^2-(b-c)^2}{(a+b)^2-c^2}=dfrac{1}{3}$,得$dfrac{a-b+c}{a+b+c}=dfrac{1}{3}$,得$a+c=2b,c=dfrac{5}{3}a$
故$angle C=dfrac{pi}{2},sin B =dfrac{b}{c}=dfrac{4}{5}$
另附上我两个同事的解答:
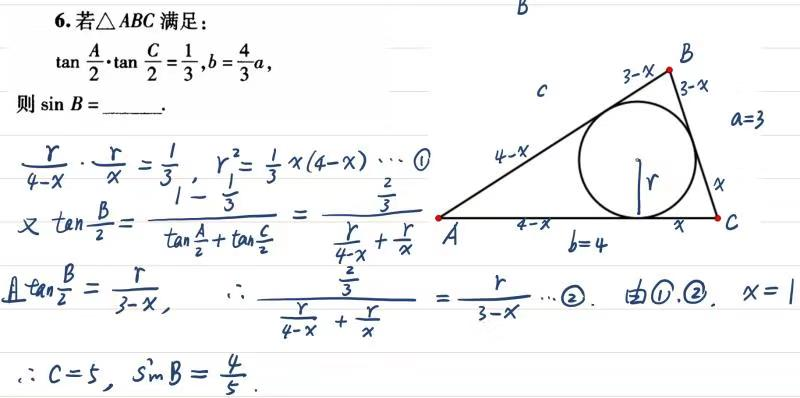
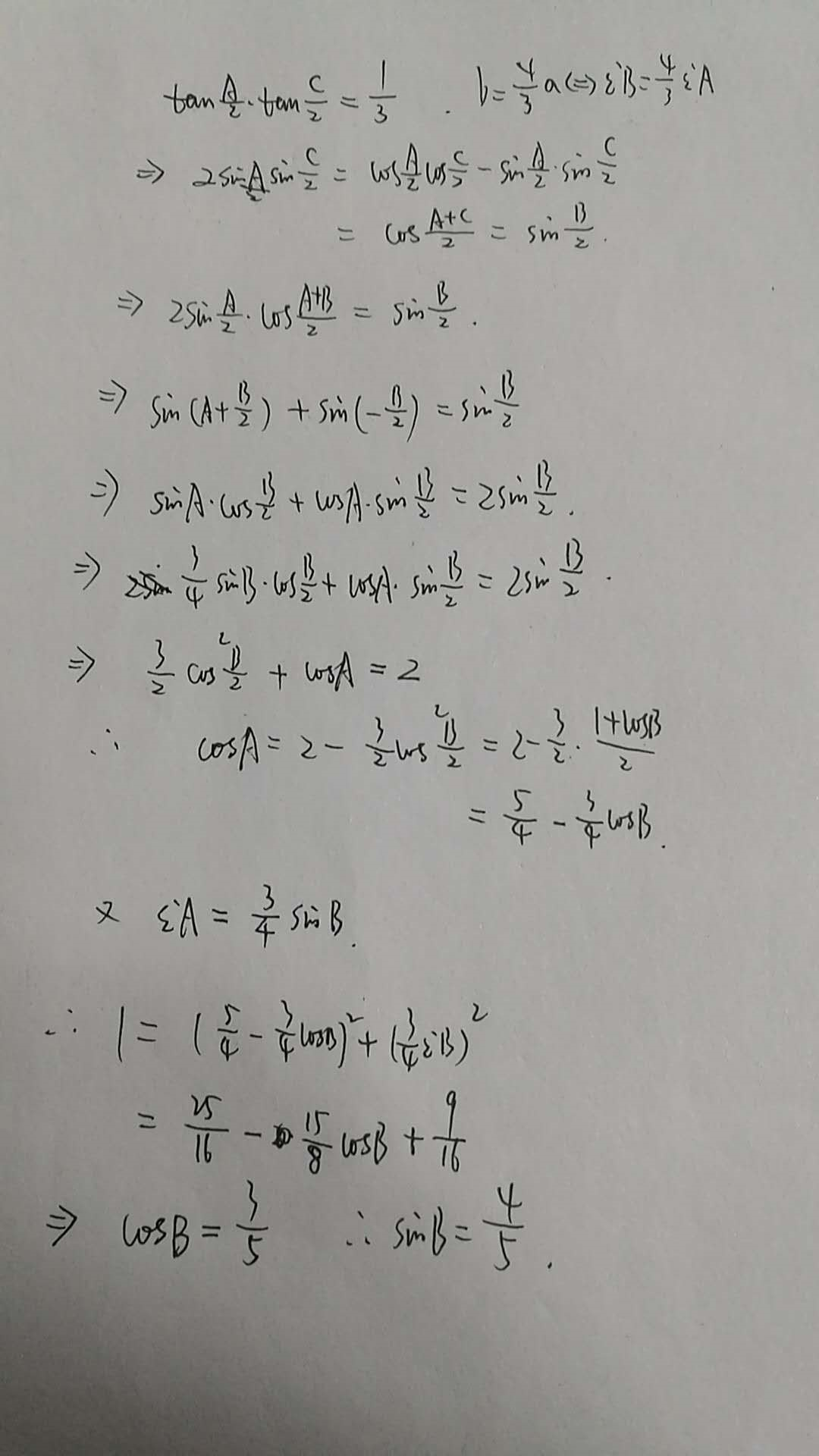
注:$sumlimits_{cyc}tandfrac{A}{2} andfrac{B}{2}=1$