Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 3228 Accepted Submission(s): 613
Problem Description
Calabash is the servant of a landlord. The landlord owns a piece of land, which can be regarded as an infinite 2D plane.
One day the landlord set up two orthogonal rectangular-shaped fences on his land. He asked Calabash a simple problem: how many nonempty connected components is my land divided into by these two fences, both finite and infinite? Calabash couldn't answer this simple question. Please help him!
Recall that a connected component is a maximal set of points not occupied by the fences, and every two points in the set are reachable without crossing the fence.
One day the landlord set up two orthogonal rectangular-shaped fences on his land. He asked Calabash a simple problem: how many nonempty connected components is my land divided into by these two fences, both finite and infinite? Calabash couldn't answer this simple question. Please help him!
Recall that a connected component is a maximal set of points not occupied by the fences, and every two points in the set are reachable without crossing the fence.
Input
The first line of input consists of a single integer T (1≤T, the number of test cases.
Each test case contains two lines, specifying the two rectangles. Each line contains four integers x1,y (0≤x1,y, where (x1,y are the Cartesian coordinates of two opposite vertices of the rectangular fence. The edges of the rectangles are parallel to the coordinate axes. The edges of the two rectangles may intersect, overlap, or even coincide.
Each test case contains two lines, specifying the two rectangles. Each line contains four integers x1,y (0≤x1,y, where (x1,y are the Cartesian coordinates of two opposite vertices of the rectangular fence. The edges of the rectangles are parallel to the coordinate axes. The edges of the two rectangles may intersect, overlap, or even coincide.
Output
For each test case, print the answer as an integer in one line.
Sample Input
3
0 0 1 1
2 2 3 4
1 0 3 2
0 1 2 3
0 0 1 1
0 0 1 1
Sample Output
3
4
2
题意:两个矩形,问这两个矩形可以将平面分割成几个部分。
思路:分析,一共可以分割为2,3,4,5,6这五种情况,4的时候情况比较多,其他四种容易
判断,所以直接判断其他四种情况即可。(比较菜,没想出来好的方法)
题目给出x1<x2,y1<y2;所以不会有非矩形的样例
设结果为ans
当ans = 6,只有这一种情况

当ans = 3时,有相离,内含的情况
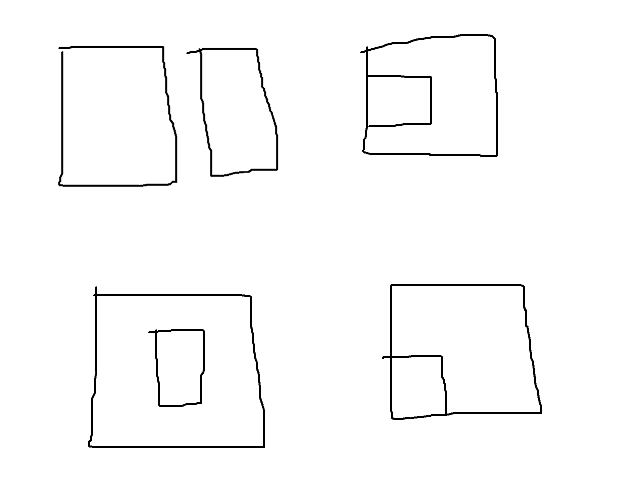
当ans = 2时,重合
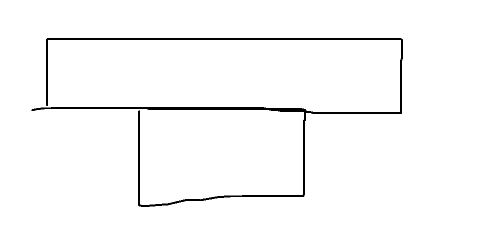
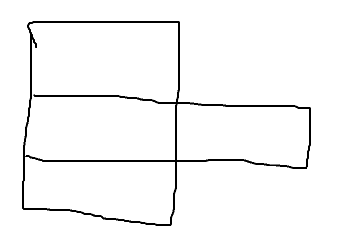
当ans = 5时,
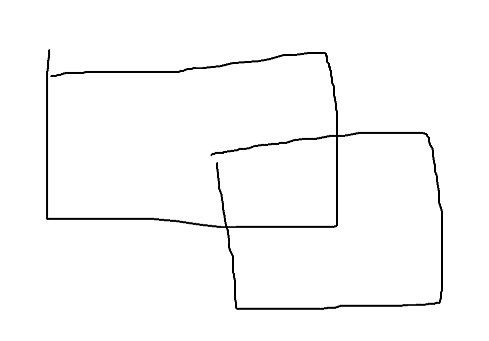
当ans = 4时,(或者还有其他的方式,else了..)
1 #include <stdio.h> 2 #include <string.h> 3 #include <iostream> 4 #include <algorithm> 5 #define int long long 6 #define rad rand()%mod+1 7 using namespace std; 8 typedef long long ll; 9 const int maxn = 1e6+5; 10 const int maxm = 1e3+5; 11 const int mod = 1e9+7; 12 13 signed main() 14 { 15 int x1, x2, x3, x4; 16 int y1, y2, y3, y4; 17 int t; 18 scanf("%lld", &t); 19 while(t--) 20 { 21 scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2); 22 scanf("%lld %lld %lld %lld", &x3, &y3, &x4, &y4); 23 ///为6的情况 24 if(x1 < x3&&x4 < x2&&y1> y3&&y2 < y4) 25 { 26 printf("6 "); 27 continue; 28 } 29 if(x3 < x1&&x2 < x4&&y3 > y1&&y2 > y4) 30 { 31 printf("6 "); 32 continue; 33 } 34 ///相离 35 if(x2 < x3||x4 < x1||y3 > y2||y1 > y4) 36 { 37 printf("3 "); 38 continue; 39 } 40 ///重合 41 if(x1 == x3&&y1 == y3&&x2 == x4&&y2 == y4) 42 { 43 printf("2 "); 44 continue; 45 } 46 ///两条边重合 47 if(x1 == x3 && x2 == x4&&((y1 < y3&&y4 < y2 )||(y1> y3&&y4 > y2))) 48 { 49 printf("4 "); 50 continue; 51 } 52 if(y1 == y3&&y2 == y4&&((x1 < x3&&x4 < x2|| (x3 < x1&&x2 < x4)) )) 53 { 54 printf("4 "); 55 continue; 56 } 57 ///内含 58 if(x1 <= x3&&x4 <= x2&&y4<=y2&&y3>=y1) 59 { 60 printf("3 "); 61 continue; 62 } 63 if(x3 <= x1&&x2 <= x4&&y1 >= y3&&y2 <= y4) 64 { 65 printf("3 "); 66 continue; 67 } 68 ///有一条边重合 (外) 69 if(x2 == x3 || x1 == x4||y2 == y3 || y1 == y4) 70 { 71 printf("3 "); 72 continue; 73 } 74 ///为5 的情况 75 if(x1 == x3) 76 { 77 if((y1 < y3 && y4 < y2) || (y1 > y3 &&y4 > y2)) 78 { 79 printf("5 "); 80 continue; 81 } 82 } 83 if(y1 == y3) 84 { 85 if((x1 < x3 && x4 < x2)||(x3 < x1&&x2 < x4) ) 86 { 87 printf("5 "); 88 continue; 89 } 90 } 91 if(x2 == x4) 92 { 93 if((y1 < y3 && y4 < y2) || (y1 > y3 && y4 > y2) ) 94 { 95 printf("5 "); 96 continue; 97 } 98 } 99 if(y2 == y4) 100 { 101 if((x1 < x3 && x4 < x2)||(x1 > x3 && x4 > x2)) 102 { 103 printf("5 "); 104 continue; 105 } 106 } 107 printf("4 "); 108 } 109 return 0; 110 } 111 112 /*** 113 114 ***/