回溯：组合问题

组合：给你一个数组，找出所有大小为2的组合。

组合是无序的！

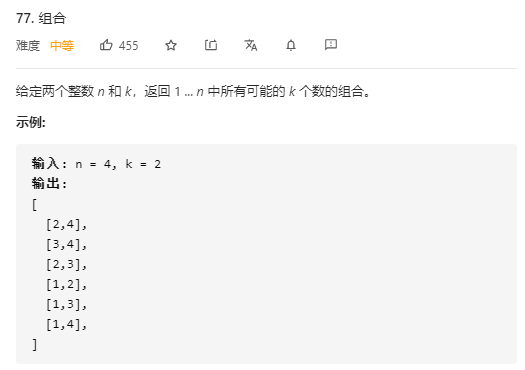
path.size()是已经选取的元素个数，还需要k-path.size()个元素需要选取，还要选取的元素至多要从n-(k-path.size())+1的位置选取。

class Solution {
private:
    vector<vector<int>> result;//存放符合条件的结果结合
    vector<int> path;//存放符合条件的单一结果
    void backtracking(int n, int k, int startIndex) {
        //回溯的终止条件:如果path数组的大小刚好等于k，说明找到了一个符合条件的结果集，存放进去
        if (path.size() == k) {
            result.push_back(path);
            return;
        }
        //for(int i=startIndex; i<=n; i++) {
            /*这个循环其实可以进行剪枝优化，因为你要求k个数的结合，那你之多也就只能遍历到结合剩下k个元素的位置，后面的遍历都是没有意义的，优化如下*/
        for (int i=startIndex; i<=(n-(k-path.size())+1); i++) {
            path.push_back(i);//处理节点
            backtracking(n, k, i+1);//递归，一直往里放，直到满足终止条件结束
            path.pop_back();//回溯，撤销处理的节点
        }
    }
public:
    vector<vector<int>> combine(int n, int k) {
        result.clear();
        path.clear();
        backtracking(n, k, 1);
        return result;
    }
};

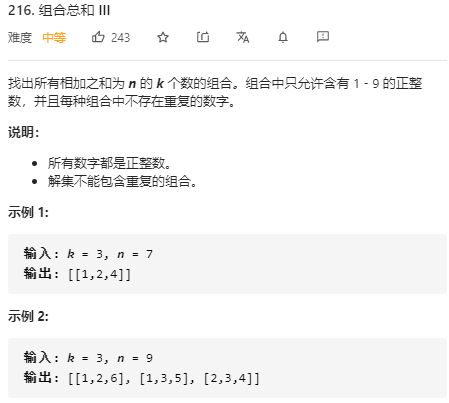
class Solution {
private:
    vector<vector<int>> result; // 用来存放结果
    vector<int> path; // 用来存放一个满足条件的路径

    void backtrackint(int k, int n, int sum, int startIndex) {
        if (sum == n) { // 如果和为n满足了条件
            if (path.size() == k) // 如果满足k个数
                result.push_back(path); // 将满足要求的一个路径path放进去
            return;
        }
        if (sum > n) // 进行剪枝，如果当前的已经大于n了，再往下比n更大
            return;

        for (int i = startIndex; i <= 9; i++) {
            path.push_back(i); // 处理当前
            sum += i;
            backtrackint(k, n, sum, i+1); // 递归
            sum -= i;
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear();
        path.clear();
        backtrackint(k, n, 0, 1);
        return result;
    }
};

 

 

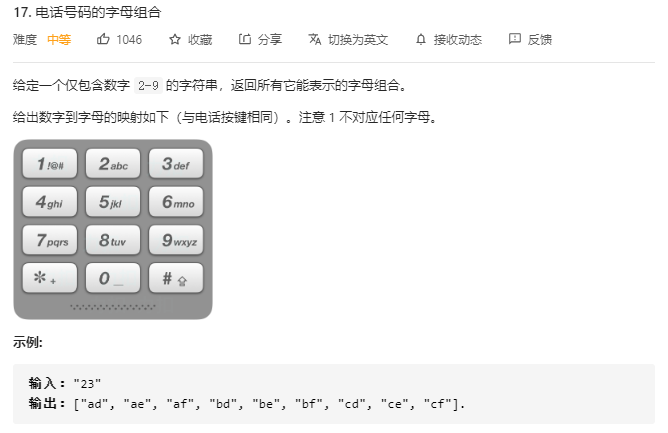
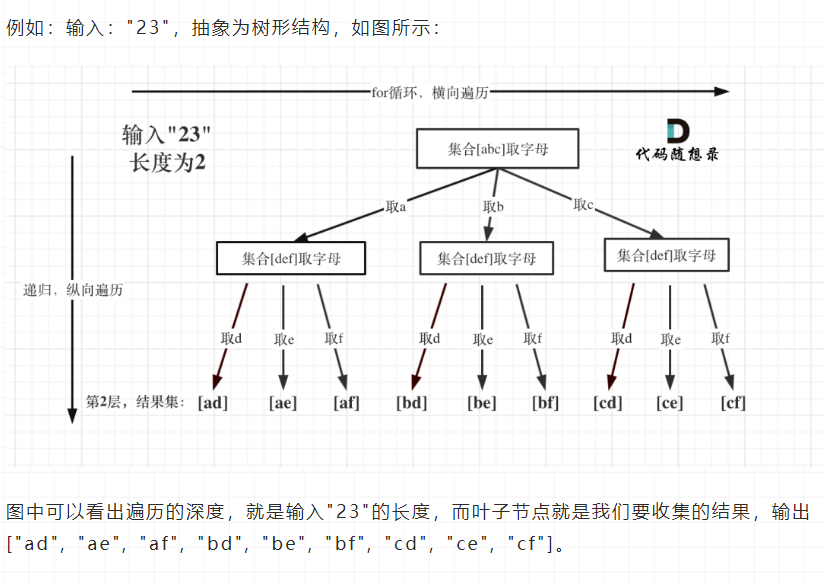
class Solution {
private:
    unordered_map<int, string> letterMap = {{2, "abc"}, {3, "def"}, {4, "ghi"}, {5, "jkl"}, {6, "mno"}, {7, "pqrs"},{8, "tuv"}, {9, "wxyz"}};
public:
    vector<string> result;
    string s;
    void backtracking(const string& digits, int index) {
        if (index == digits.size()) {//每个组合的字符串当中有digits.size()个元素
            result.push_back(s);
            return;
        }
        int digit = digits[index] - '0';//将index位置对应的字符转换成Int
        string letters = letterMap[digit]; //取出digit对应的字符集
        for (int i=0; i<letters.size(); i++) {
            s.push_back(letters[i]);
            backtracking(digits, index+1); //递归，注意index+1，要处理下一个数字了
            s.pop_back(); //回溯
        }
    }
    vector<string> letterCombinations(string digits) {
        result.clear();
        s.clear();
        if (digits.size() == 0) {
            return result;
        }
        backtracking(digits, 0);
        return result;
    }
};

 

 

 startIndex很重要，组合问题不能有重复，只能向后取！

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        if (sum > target) // 因为数组中元素都是正整数，所以可以剪枝
            return;
        
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) { // &&后面的是剪枝，意思是在当前层中，如果下一层的sum（就是本层的sum加上candidates[i]）已经大于target了，就没必要继续往下了
            path.push_back(candidates[i]);
            sum += candidates[i];
            backtracking(candidates, target, sum, i); // 这里的i是重点！！！体现了可以重复！！！
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        if (candidates.empty())
            return {};
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0);
        return result;
    }
};
// 求和问题中，排序之后加剪枝是常见的套路！
// 什么时候用startIndex，什么时候不用：如果是一个集合来求组合的话，就需要startIndex；如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex
// 元素可被无限重复选取表现在代码里
// 剪枝方法

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex, vector<bool>& used) {
        if (sum == target) {
            result.push_back(path);
            return;
        }
        if (sum > target) {
            return;
        }
        for (int i=startIndex; i<candidates.size() && (sum + candidates[i]) <= target; i++) {
            /*如果candidates[i] == candidates[i-1]并且used[i-1] == 1的话，说明元素在同一个树枝里使用过，这是允许的
            *如果candidates[i] == candidates[i-1]并且used[i-1] == 0的话，说明元素在同一树层里重复了，这是不允许的，要进行去重
            */
            if (i>0 && candidates[i] == candidates[i-1] && used[i-1] == false) {
                continue;
            }
            sum += candidates[i];
            path.push_back(candidates[i]);
            used[i] = true;
            backtracking(candidates, target, sum, i+1, used); // 这里是i+1不是i
            used[i] = false;
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        vector<bool> used(candidates.size(), false); // 用这数组来进行去重
        sort(candidates.begin(), candidates.end()); // 先把数组排序，让相同的元素排在一起，这样才能后面去重
        backtracking(candidates, target, 0, 0, used);
        return result;
    }
};