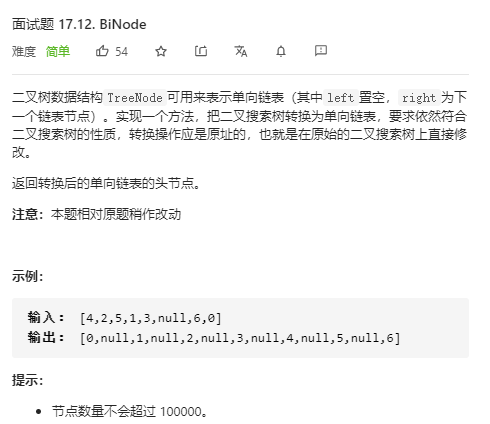
/******************************************/
二叉树的问题,一定要明白到底应该深度优先(前中后序)还是广度优先(层序遍历)
最基本的遍历方式:深度优先和广度优先
深度优先:前、中、后序(递归法和迭代法均可)
广度优先:层次遍历(迭代法)
栈其实就是递归的一种实现结构,也就是说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的;
广度优先遍历(层序遍历)的实现一般使用队列来实现,这也是队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。力扣102题
递归算法的三要素:
-
「确定递归函数的参数和返回值:」确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
-
「确定终止条件:」写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
-
「确定单层递归的逻辑:」确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程
二叉树节点的定义框架:
struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} };
二叉树相关的题目永远都逃不开树的递归遍历框架:
/*二叉树的遍历框架*/ void traverse(TreeNode root) { //前序遍历:先访问根节点,再前序访问左子树,再访问右子树 traverse(root->left); //中序遍历:先中序访问左子树,再访问根节点,再访问右子树 traverse(root->right); //后续遍历:先后续访问左子树,再访问右子树,再访问根节点 }
快速排序其实就是二叉树的前序遍历。
快速排序的逻辑是,需要对一个数组进行排序,我知道数组的首地址,知道首元素和最后一个元素的下标,然后我就先找一个分界点p,通过交换元素使得分界点p左边的值都比p小,右边的都比p大,然后递归的去这样做,最后整个数组就被排序了。这里需要知道的是,分界点p是数组的下标,怎么得到呢,我们在执行“分”的这个操作的时候,是先选取了一个基准值,一般选的是数组最后一个元素,当然优化的方式更好是随机选择的,选好基准值后,通过循环判断将比基准值小的都往左边放,最后将基准值放到数组合适的位置,这个位置的下标就是分界点p了。得到p之后,递归的对p左边的子数组和p右边的子数组进行排序,传入的参数是数组的首地址,子数组的首元素和尾元素下标,这个根据p得到。
代码框架如下:
void sort(vector<int>& nums, int lo, int hi) { /*前序遍历位置*/ //通过交换元素构建分界点p int p = partition(nums, lo, hi); /***********************/ sort(nums, lo, p - 1); sort(nums, p + 1, hi); }
归并排序其实就是二叉树的后序遍历。
归并排序的逻辑是,需要对一个数组进行排序,我知道数组的首地址,知道首元素和最后一个元素的下标,然后我将数组一分为二,分别对左右子数组进行排序,所以应该先求一个mid,以便于将数组通过下标分开,然后递归进行左右子数组排序,最后,将这两个有序数组进行合并,整个数组就排好了,合并的时候,是将两个有序的子数组合并起来,需要将两个数组从头开始比较元素,构建一个新的容器暂存有序的数组,一直保持将小的先放进去的原则,放完之后,肯定有一个子数组完全放进去了,还有一个是没有的,所以需要进行判断,将剩下的放进去。
代码框架如下:
void sort(vector<int>& nums, int lo, int hi) { int mid = (lo + hi) / 2; sort(nums, lo, mid - 1); sort(nums, mid + 1, hi); /*后序遍历位置*/ //合并两个排好序的子数组 merge(nums, lo, mid, hi); /*****************/ }
写递归算法的秘诀:关键是要明确函数的定义是什么,然后相信这个定义,利用这个定义推到最终的结果,千万不能跳进递归的细节。
关于二叉树的题目基本都是用递归很容易解决,问题是,你要搞清楚,这个题目当中,相当于让每个节点干什么事情。
二叉树的前序遍历:迭代和递归
class Solution { public: //vector<int> result;//递归的话定义在这里 vector<int> preorderTraversal(TreeNode* root) { //递归方式 /* if(root == nullptr) return {}; result.push_back(root->val); preorderTraversal(root->left); preorderTraversal(root->right); return result; */ //当然可以使用迭代解法,因为递归本身就是用栈来实现的,可以通过栈来迭代操作 //但是要注意栈的特性是后入先出,前序的话,就是先放入根节点赋值操作弹出,再放入右节点、左节点,再弹出,这样左节点就会先出,先赋值操作,就是前序了 stack<TreeNode*> sta; vector<int> result; sta.push(root); while(!sta.empty()) { int size = sta.size(); for(int i=0; i<size; i++) { TreeNode* node = sta.top(); sta.pop(); result.push_back(node->val); if(node->right) sta.push(node->right); if(node->left) sta.push(node->left); } } return result; } };
二叉树的后序遍历:迭代和递归
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //vector<int> result;//递归解法定义在这里 vector<int> postorderTraversal(TreeNode* root) { /* if(root == nullptr) return {}; postorderTraversal(root->left); postorderTraversal(root->right); result.push_back(root->val); return result; */ //本题还可以采用迭代解法,因为递归就是用栈来实现的 //考虑实现的过程 //后序遍历是左右中的顺序,但是我们在迭代的时候肯定会先访问根节点,也就是中间的节点,所以考虑先访问和处理中间节点,再处理右节点,再处理左边节点,最后将结果翻转就行了 stack<TreeNode*> sta; vector<int> result; sta.push(root); while(!sta.empty()) { int size = sta.size(); for(int i=0; i<size; i++) { TreeNode* node = sta.top(); sta.pop(); result.push_back(node->val); if(node->left) sta.push(node->left); if(node->right) sta.push(node->right); } } reverse(result.begin(), result.end()); return result; } };
二叉树的中序遍历
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: //vector<int>result;//递归写法这里定义 vector<int> inorderTraversal(TreeNode* root) { /*递归解法 if(root == nullptr) return {}; inorderTraversal(root->left); result.push_back(root->val); inorderTraversal(root->right); return result; */ //还能采用迭代解法,用栈来解决,因为递归本身就是用栈来实现的,因此是完全行得通的 //中序的顺序是左中右,那出栈的时候,处理的顺序肯定是右中左 //搞清楚访问和处理的概念 //访问:将节点入栈 //处理:将节点的值放入结果集 //中序的访问和处理的顺序是不一样的,所以要借助指针进行访问,也就是将节点放入栈中,用栈来做处理,也就是放入结果集 vector<int> result; stack<TreeNode*> sta; TreeNode* cur = root; while(cur != nullptr || !sta.empty()) { if(cur != nullptr) {//指针用来访问节点,访问到左边最底层的时候,指针和要开始处理的位置就一样了 sta.push(cur);//将访问的节点放进栈 cur = cur->left;//最左的子节点最后放进去,所以会先出栈 左 } else { cur = sta.top(); sta.pop(); result.push_back(cur->val); //中 cur = cur->right; //右 } } } };

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { queue<TreeNode*> que;//创建一个队列,层序遍历树的需要用队列来实现,队列中是二叉树的节点 if(root != nullptr) que.push(root);//如果头结点不为空的话,先将头结点放到队列中,因为头结点也就是第一行,只有这一个元素,所以直接放进去 vector<vector<int>> result;//定义返回值,返回的是一个二维数组 while(!que.empty()) { int size = que.size();//同一行可能不止一个元素,要循环都进行遍历,又因为下面要进行pop操作,que.size()是一个变化的值,所以这里存储数量 vector<int> vec;//用于临时存储每一行的节点值,最后统一存入返回的二维数组中 for(int i=0; i<size; i++) { TreeNode* node = que.front(); que.pop();// vec.push_back(node->val); if(node->left) que.push(node->left);//将这个节点的左右子节点放入队列中 if(node->right) que.push(node->right); } result.push_back(vec); } return result; } };
掌握了层序遍历的模板,别的题只要稍微改动几行代码就可以解决了。
遇到二叉树的题目,一定要想一想到底是用深度优先遍历还是广度优先遍历,到底使用迭代法还是用递归法。
遇到求二叉树节点的数量以及求二叉树的深度相关的题目,使用迭代和递归方法均可,关键是要自动向下对问题进行分析。
226.翻转二叉树

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode* invertTree(TreeNode* root) { //通过分析,得到了题意是:将每个节点的左右子节点进行翻转就可以了,前序和后序的方式都行 //不能使用中序的原因是某些节点可能会被翻转两次 /* if(root == NULL) return root; swap(root->left, root->right); invertTree(root->left); invertTree(root->right); return root; */ //以上是递归写法,这道题还可以有迭代写法,反正知道了题意就是将每个节点的左右子节点进行互换就可以了,可以遍历每个节点进行操作 /* if(root == NULL) return root; stack<TreeNode*> st; st.push(root); while(!st.empty()) { TreeNode* node = st.top(); st.pop(); swap(node->left, node->right); if(node->right) st.push(node->right); if(node->left) st.push(node->left); } return root; */ //以上是深度优先遍历当中的前序迭代写法,还可以采用层序遍历 if(root == NULL) return root; queue<TreeNode*> que; que.push(root); while(!que.empty()) { int size = que.size(); for(int i=0; i<size; i++) { TreeNode* node = que.front(); que.pop(); swap(node->left, node->right); if(node->left) que.push(node->left); if(node->right) que.push(node->right); } } return root; } };
114.二叉树展开为链表

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: void flatten(TreeNode* root) { //后序遍历:在还没操作节点右子树前,不能破坏该节点的右子树指向 if(root == nullptr) return; flatten(root->left); flatten(root->right); //左右子树已经被拉平成一条链表,需要将左子树变成右子树,将原来的右子树节点接到后面 TreeNode* left = root->left; TreeNode* right = root->right; root->left = nullptr; root->right = left; TreeNode* p = root; while(p->right != nullptr) { p = p->right; } p->right = right; } };
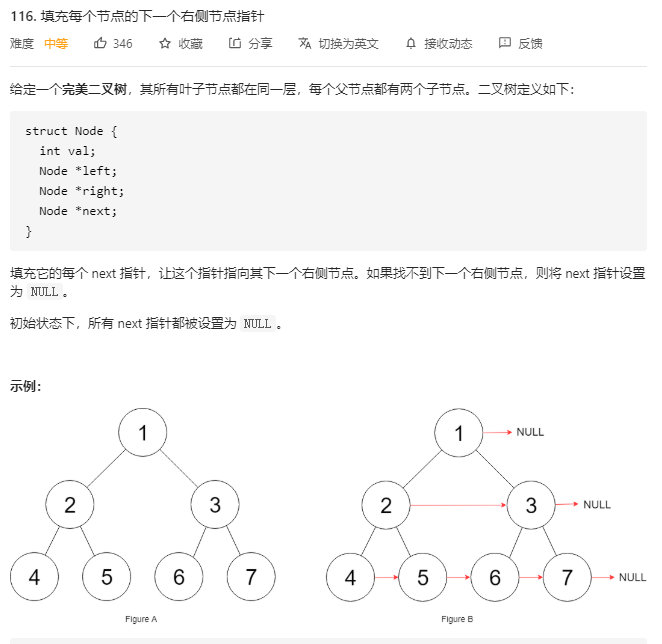
/* // Definition for a Node. class Node { public: int val; Node* left; Node* right; Node* next; Node() : val(0), left(NULL), right(NULL), next(NULL) {} Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {} Node(int _val, Node* _left, Node* _right, Node* _next) : val(_val), left(_left), right(_right), next(_next) {} }; */ class Solution { public: Node* connect(Node* root) { if(root == nullptr) return nullptr; connectTwoNode(root->left, root->right); return root; } void connectTwoNode(Node* node1, Node* node2) { if(node1 == nullptr || node2 == nullptr) return;//不操作 node1->next = node2; connectTwoNode(node1->left, node1->right); connectTwoNode(node2->left, node2->right); connectTwoNode(node1->right, node2->left); } };
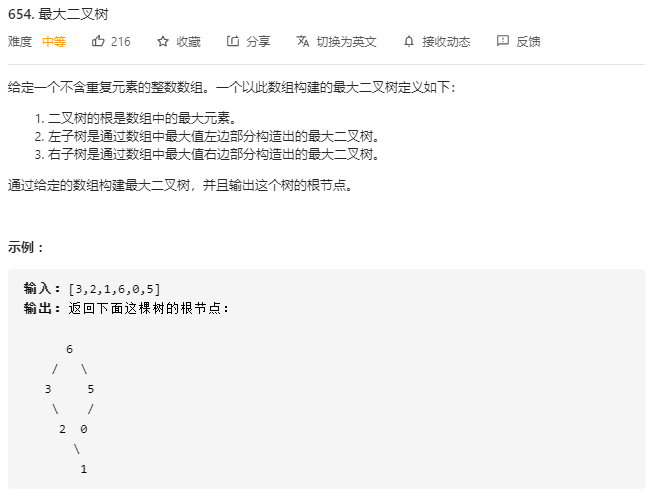
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode* constructMaximumBinaryTree(vector<int>& nums) { //肯定是需要先知道这个最大值,构造根节点,然后递归的构造左右子树,采用前序遍历框架 //需要知道子数组,所以函数的参数不够,需要自己构造函数,传入数组、子数组头尾下标 return build(nums, 0, nums.size()-1); } TreeNode* build(vector<int>& nums, int lo, int hi) { if(lo > hi) return nullptr; /*下面这一段是求最大值和最大值索引的,时间复杂度为O(n)*/ int max_num = nums.at(0); int index = 0; for(int i=0;i<=hi;i++) { if(max_num < nums.at(i)) { max_num = nums.at(i); index = i; } } /*****************************/ TreeNode* head = new TreeNode(max_num); head->left = build(nums, 0, index); head->right = build(nums, index+1, hi); return head; } };
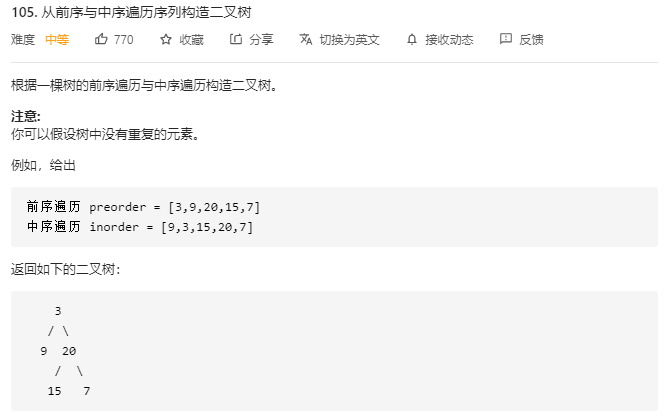
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { //要先明白,构造一颗二叉树,首先你得构造出根节点吧,然后你再去构造左右子节点 //根节点简单,就是前序遍历的第一个元素,很容易能够构造 //关键是你要构造左右子节点以及往下的,你得知道哪些元素是左子树哪些是右子树的,这就需要通过中序序列和已知的根节点的值来确定,这是中序的特性 return build(preorder, 0, preorder.size()-1, inorder, 0, inorder.size()-1); } TreeNode* build(vector<int> preorder, int prestart, int preend, vector<int> inorder, int instart, int inend) { if(prestart > preend) return nullptr; //先保存根节点的值,找到中序序列中根节点的位置 int rootval = preorder.at(prestart); int index = 0; for(int i=instart;i<=inend;i++) { if(inorder.at(i) == rootval) { index = i; break; } } //以上找到了中序序列中根节点的位置index int leftSize = index - instart;//得到左子树节点的个数,因为要分开前序遍历序列 //先构造根节点 TreeNode* root = new TreeNode(rootval); //递归构造 root->left = build(preorder, prestart+1, index+leftSize, inorder, instart, index-1); root->right = build(preorder, prestart+leftSize+1, preend, inorder, index+1, inend); return root; } };

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) { //后序和中序跟前一个一样的道理,还是应该先构造头结点,然后递归构造左右子树 //需要新建一个函数进行数组起止位置控制,别的也没什么 //后序最后一个是根节点的值 return build(inorder, 0, inorder.size()-1, postorder, 0, postorder.size()-1); } TreeNode* build(vector<int>& inorder, int inStart, int inEnd, vector<int>& postorder, int postStart, int postEnd) { //base case if(inStart > inEnd) return nullptr; //先保存根节点的值 int rootVal = postorder.at(postEnd); int index = 0;//记录中序序列中根节点的位置 for(int i=inStart;i<=inEnd;i++) { if(inorder.at(i) == rootVal) { index = i; break; } } int leftSize = index - inStart; //构造根节点 TreeNode* root = new TreeNode(rootVal); //递归构造左右子树 root->left = build(inorder, inStart, index-1, postorder, postStart, postStart+leftSize-1); root->right = build(inorder, index+1, inEnd, postorder, postStart+leftSize, postEnd-1); return root; } };

/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool isSubStructure(TreeNode* A, TreeNode* B) { //第一步:在树A中找到和树B的根节点一样的节点R //第二步:判断树A中以R为根节点的子树是不是包含和树B一样的结构 bool result = false; if(A != nullptr && B != nullptr)//只有两个都不空才去判断 { if(equal(A->val, B->val)) { //如果找到了跟B节点的根节点一样的节点,就去判断第二步 result = doesTree1HaveTree2(A, B); } if(!result) { //如果当前节点跟B根节点不一样,就去递归判断当前节点的左节点 result = isSubStructure(A->left, B); } if(!result) { //如果当前节点跟B根节点不一样,就去递归判断当前节点的右节点 result = isSubStructure(A->right, B); } } return result; } bool doesTree1HaveTree2(TreeNode* pRoot1, TreeNode* pRoot2) { if(pRoot2 == nullptr) { return true; } if(pRoot1 == nullptr) { return false; } if(!equal(pRoot1->val, pRoot2->val)) { return false; } return doesTree1HaveTree2(pRoot1->left, pRoot2->left) && doesTree1HaveTree2(pRoot1->right, pRoot2->right);//判断子树是不是一样的 } bool equal(double b1, double b2)//定义double类型是不是相等的判断 { if(b1-b2<0.0000001 && b1-b2>-0.0000001) return true; else return false; } };

(1)有一道求二叉树深度的题目,那个题目写的求深度的算法可以应用到这道题目里,思路就是,求得每一个结点的左右子节点的深度,判断相差不超过1,则是平衡二叉树
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool isBalanced(TreeNode* root) { if(root == nullptr) return true; //分别得到左右深度 int left = maxDepth(root->left); int right = maxDepth(root->right); if(left-right<-1 && left-right>1) return false; return isBalanced(root->left) && isBalanced(root->right); } int maxDepth(TreeNode* pRoot) { //求以pRoot为根节点的二叉树深度 if(pRoot == nullptr) return 0; int left = maxDepth(pRoot->left); int right = maxDepth(pRoot->right); return left>right? (left+1) : (right+1); } };
(2)每个节点只遍历一次的做法
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool isBalanced(TreeNode* root) { //用后序遍历的方式,遍历到一个节点之前我们就已经遍历了它的左右子树。在遍历每个节点的时候记录它的深度 int pDepth; return itIsBalanced(root, &pDepth); } bool itIsBalanced(TreeNode* pRoot, int* pDepth) { if(pRoot == nullptr) { *pDepth = 0; return true; } int left, right; if(itIsBalanced(pRoot->left, &left) && itIsBalanced(pRoot->right, &right))//判断当前节点的左右子节点为根节点的树是不是平衡的 { int diff = left - right; if(diff<=1 && diff>=-1)//判断当前节点为根节点的二叉树是不是平衡的 { *pDepth = 1 + (left>right ? left : right); return true; //如果子节点为根节点的是平衡的,当前节点为根节点的是平衡的,整个就是平衡的 } } return false; } };
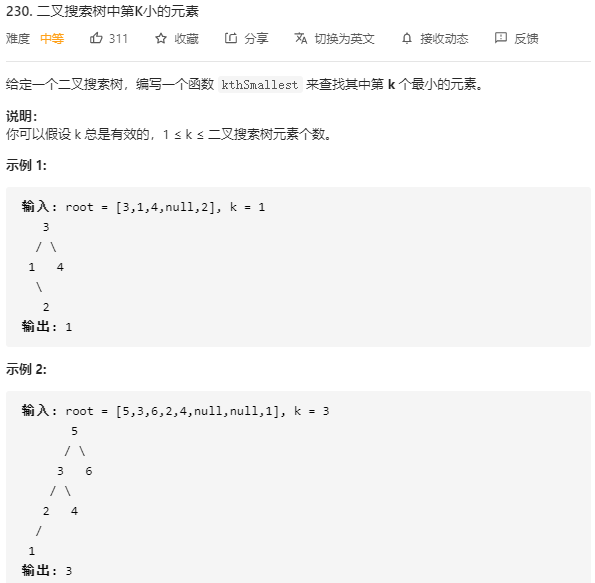
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int kthSmallest(TreeNode* root, int k) { //后序遍历,二叉搜索树的后序遍历是有序的 traverse(root, k); return res; } int res = 0;//记录结果 int rank = 0;//记录当前元素的位置排序 void traverse(TreeNod* root, int k) { if(root == nullptr) return; traverse(root->left, k); rank++; if(k == rank) { res = root->val; return; } traverse(root->right, k); } };
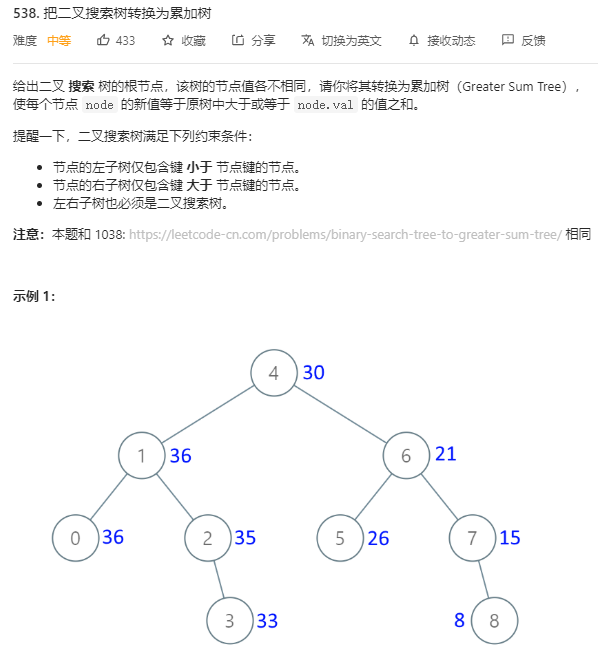
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* convertBST(TreeNode* root) { traverse(root); return root; } //记录累加和 int sum = 0; void traverse(TreeNode* root) { if(root == nullptr) return; traverse(root->right); //维护累加和 sum += root->val; //将BST转化成累加树 root->val = sum; traverse(root->left); } };