之前一直在复习树的相关知识,后来在leetcode中做了八道题目,这些题目不像之前二分查找一样有很多的细节,更多的只是看你的解题思路和树的基础操作,还有就是对递归的掌握程度。这八道题目总共可以分为三类,一类就是对一般树进行操作,主要就是提出一些要求,让你实现,第二类就是对树进行不同的方式遍历,第三就是平衡树、排序树的验证和增删改查。本文所有代码都放在我的github。
普通树的要求
这种题目给出的树,都是二叉树,对二叉树进行一些操作,大多数都是查找,只不过查找不是节点这种简单要求,而是最大路径、节点的共同祖先等等奇怪的要求。这类题目一般都是需要好的解题思路。
leetcode,第104题,Maximum Depth of Binary Tree,
Given a binary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example:
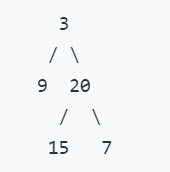
Given binary tree [3,9,20,null,null,15,7],
return its depth = 3.
这道题目就是求树的深度,深度主要是看叶子节点,所以这道题第一想到的就是如果我用递归的思想的话,一直到叶子节点,之后从叶子节点回溯的时候,依次加上1,然后看左右节点谁的深度最大,那么该节点的深度就是谁。这道题的思路还是比较清晰,主要是要熟悉递归写法。
// 这个方法很快,并且空间也不大
public int maxDepth(TreeNode root) {
// 这个节点就是空节点
if(root == null) return 0;
if(root.left != null || root.right != null) {
int left_depth = 1;
int right_depth = 1;
if(root.left != null) {
left_depth = maxDepth(root.left) + 1;
}
if(root.right != null) {
right_depth = maxDepth(root.right) + 1;
}
return Math.max(left_depth, right_depth);
}else {
return 1;
}
}
leetcode,第124题,Binary Tree Maximum Path Sum,
Given a non-empty binary tree, find the maximum path sum.
For this problem, a path is defined as any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The path must contain at least one node and does not need to go through the root.
Example:
Input:[-10,9,20,null,null,15,7]
Output: 42
这道题目还是有点难度的,求的最长路径,上图就是节点15到节点7的路径最长是42。依旧是用递归的思想来推导,以一个-10节点为例,这里的情况就是左子树最大,或者右子树最大,左子树加节点最大,右子树加节点最大,左子树加右子树加节点最大,这里其实不管谁最大,那么如果有一方是负数,那么肯定就不加它,比如节点-10,那么肯定不加节点-10,在代码可以将之与0比较即可,那么左子树和右子树如何比较大小,那么就设置一个全局变量进行比较。还要考虑递归的返回值是多少,递归返回值也就是子树的最大路径长度,那么子节点只能从左子树和右子树中选出一个才能和父节点形成一条路径,因此递归的返回值是左子树和右子树中较大的那个。
// 使用递归的思想来做,这里返回是路径的话。你只能选择其中一条路走
// 但是在求最大路径的时候,就可以三个都加起来
// 负数被省去了,那么左右子树就不会是负数,
private int searchMaxPathSum(TreeNode root) {
if(root == null) return 0;
int left_sum = Math.max(searchMaxPathSum(root.left),0);
int right_sum = Math.max(searchMaxPathSum(root.right),0);
// 包含了左子树加节点最大,右子树加上节点最大,左右子树是最大的,左右子树相加外加节点是最大的
max_path_sum = Math.max(left_sum + right_sum + root.val,max_path_sum);
return Math.max(left_sum, right_sum) + root.val;
}
leetcode,第236题,Lowest Common Ancestor of a Binary Tree,
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
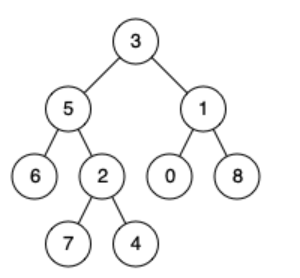
Given the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]
Example:
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
这道题就是找给出节点的共同祖先,节点也可以是自己的祖先。思想并不难,就是肯定只有三种情况:
- 俩个节点都在左子树或者右子树中,那么我们还需要继续查找。
- 俩个节点分别在左子树和右子树中,那么祖先肯定就是该节点。
- 该节点就是其中一个要查找的节点,那么祖先肯定就是该节点。
按照这个思路,我开始的代码非常的复杂。
// 这种写法很慢很慢。思想是对的,但是写法过于复杂了。
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
boolean isOneContain = true;
while(isOneContain) {
if(root == p || root == q) {
isOneContain = false;
break;
}
boolean isLeft = searchNodeValue(root.left, p, q);
boolean isRight = searchNodeValue(root.right, p, q);
if(isLeft && isRight) {
isOneContain = false;
}else {
root = isLeft?root.left:root.right;
}
}
return root;
}
private boolean searchNodeValue(TreeNode rootNode, TreeNode p, TreeNode q) {
if(rootNode == p || rootNode == q) {
return true;
}
if(rootNode == null) {
return false;
}
boolean left = searchNodeValue(rootNode.left, p, q);
boolean right = searchNodeValue(rootNode.right, p, q);
if(left || right) {
return true;
}else {
return false;
}
}
上面的代码没有用递归,如果用递归,那么代码量没有这么多,只要检查几种情况就行了。
// 思想和上面一样,都是看节点,只不过上面是查找,
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == p || root == q || root == null) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
//----------优化-------------------------------
// 加上他反而变慢了,主要是为了返回如果不是p也不是q,也不是null,那肯定就是最小父节点,那么不用递归右节点了,不过反而慢了
// if(left != null && left != p && left != q) return left;
//-------------------------------
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left != null && right != null) return root;
return left == null?right:left;
}
树的遍历
这类题目就是遍历的一些变形要求,让你使用不同的顺序来遍历树,不管它怎么要求,其实遍历的方法就那几种,还有一个就是排序树的中序遍历是从小到大完全有序,不过下面几个都是BFS层次遍历。
leetcode,第102题,Binary Tree Level Order Traversal,
Given a binary tree, return the level order traversal of its nodes' values. (ie, from left to right, level by level).
Example:
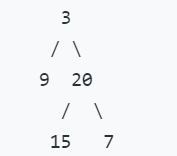
Given binary tree [3,9,20,null,null,15,7],
return its level order traversal as:
[
[3],
[9,20],
[15,7]
]
这个说白了就是一个层次遍历,层次遍历使用的是队列,只不过每次处理队列的时候,将队列中的数据全部取出来处理就行了。
// 层次遍历
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> tree_list = new ArrayList<List<Integer>>();
if(root == null) return tree_list;
Queue<TreeNode> tree_queue = new LinkedList<TreeNode>();
tree_queue.offer(root);
while(!tree_queue.isEmpty()) {
List<Integer> one_list = new ArrayList<Integer>();
int queue_size = tree_queue.size();
int index = 0;
while(index < queue_size) {
TreeNode one_node = tree_queue.poll();
one_list.add(one_node.val);
if(one_node.left != null) tree_queue.offer(one_node.left);
if(one_node.right != null) tree_queue.offer(one_node.right);
index++;
}
tree_list.add(one_list);
}
return tree_list;
}
leetcode,第107题,Binary Tree Level Order Traversal II,
Given a binary tree, return the bottom-up level order traversal of its nodes' values. (ie, from left to right, level by level from leaf to root).
Example:
Given binary tree [3,9,20,null,null,15,7],
return its bottom-up level order traversal as:
[
[15,7],
[9,20],
[3]
]
这道题说是上面的第二版本,其实就是将上面层次遍历的顺序颠倒一下,我上网查过了,好像没有什么好的解法。
// 没啥好的写法,大家都是这种翻转过来
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> tree_list = new ArrayList<List<Integer>>();
if(root == null) return tree_list;
Queue<TreeNode> tree_queue = new LinkedList<TreeNode>();
tree_queue.offer(root);
while(!tree_queue.isEmpty()) {
List<Integer> one_list = new ArrayList<Integer>();
int queue_size = tree_queue.size();
int index = 0;
while(index < queue_size) {
TreeNode one_node = tree_queue.poll();
one_list.add(one_node.val);
if(one_node.left != null) tree_queue.offer(one_node.left);
if(one_node.right != null) tree_queue.offer(one_node.right);
index++;
}
tree_list.add(0, one_list);
}
return tree_list;
}
leetcode,第103题,Binary Tree Zigzag Level Order Traversal,
Given a binary tree, return the zigzag level order traversal of its nodes' values. (ie, from left to right, then right to left for the next level and alternate between).
Example:
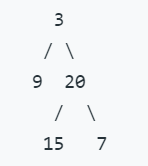
Given binary tree [3,9,20,null,null,15,7],
return its zigzag level order traversal as:
[
[3],
[20,9],
[15,7]
]
这种叫做Z遍历,就是如果上面是从左到右的顺序,那么下面就是从右到左的顺序,本质也是层次遍历,也不难,就是设置一个判断条件,看它的顺序是什么即可。
// 遍历
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> tree_list = new ArrayList<List<Integer>>();
if(root == null) return tree_list;
Queue<TreeNode> tree_queue = new LinkedList<TreeNode>();
tree_queue.offer(root);
boolean leftToRight = true;
while(!tree_queue.isEmpty()) {
List<Integer> one_list = new ArrayList<Integer>();
int queue_size = tree_queue.size();
int index = 0;
while(index < queue_size) {
TreeNode one_node = tree_queue.poll();
// 就是层次遍历上加一个判断条件
if(leftToRight) {
one_list.add(one_node.val);
}else {
one_list.add(0, one_node.val);
}
if(one_node.left != null) tree_queue.offer(one_node.left);
if(one_node.right != null) tree_queue.offer(one_node.right);
index++;
}
leftToRight = !leftToRight;
tree_list.add(one_list);
}
return tree_list;
}
特殊树的操作
leetcode中特殊树,比如AVL和BST挺多的,大多数都是插入删除这种操作,之前都已经实现了,就没贴出来,选了下面这俩道,一个判断是不是BST,还有一个是判断是不是平衡树。
leetcode,第98题,Validate Binary Search Tree,
Given a binary tree, determine if it is a valid binary search tree (BST).
Assume a BST is defined as follows:
The left subtree of a node contains only nodes with keys less than the node's key.
The right subtree of a node contains only nodes with keys greater than the node's key.
Both the left and right subtrees must also be binary search trees.
Example:
Input: [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.
判断BST,就是左子树所有节点小于该节点,右子树所有节点大于该节点,那么只需要递归的时候每次找出左子树的最大和右子树的最小值进行比较,我写了一下,没有优化,代码还是很复杂。
// 1. 找出左子树最小值和右子树的最大值来比较,分治法,但是复杂度太高了
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
if((root.left != null && root.val <= findMax(root.left)) ||
(root.right != null && root.val >= findMin(root.right))) {
return false;
}
boolean isLeft = isValidBST(root.left);
boolean isRight = isValidBST(root.right);
return isLeft&&isRight;
}
private int findMax(TreeNode node) {
int max_value = node.val;
Queue<TreeNode> tree_queue = new LinkedList<TreeNode>();
tree_queue.offer(node);
while(!tree_queue.isEmpty()) {
TreeNode one_node = tree_queue.poll();
if(max_value < one_node.val) max_value = one_node.val;
if (one_node.left != null)
tree_queue.offer(one_node.left);
if (one_node.right != null)
tree_queue.offer(one_node.right);
}
return max_value;
}
private int findMin(TreeNode node) {
int min_value = node.val;
Queue<TreeNode> tree_queue = new LinkedList<TreeNode>();
tree_queue.offer(node);
while(!tree_queue.isEmpty()) {
TreeNode one_node = tree_queue.poll();
if(min_value > one_node.val) min_value = one_node.val;
if (one_node.left != null)
tree_queue.offer(one_node.left);
if (one_node.right != null)
tree_queue.offer(one_node.right);
}
return min_value;
}
上面的代码量挺多的,主要是查找左子树和右子树的最值上花了很多代码。但是如果将思维转化一下,该节点是左子树的最大值和右子树的最小值,那么我们使用递归,依次比较即可。
// 2. 上面有简化版,不过思想变了一下,就是根节点是左子树的最大值,右子树的最小值,这个效率高
public boolean isValidBST(TreeNode root) {
// 这是因为输入可能是,[2147483647]
if(root == null) return true;
return validBst(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean validBst(TreeNode root, long min_value, long max_value) {
if(root == null) return true;
if(root.val <= min_value || root.val >= max_value) return false;
return validBst(root.left, min_value, root.val) && validBst(root.right, root.val, max_value);
}
判断BST,之前我们说过中序遍历BST,那么出来就是一个从小到大的有序序列,我们对树进行中序遍历即可,如果使用非递归中序遍历,可以直接将节点与上一次访问节点进行比较即可。
// 4. 也可以使用非递归中序遍历,这样的话,还可以直接比较是不是比前面大,不用存储
public boolean isValidBST(TreeNode root) {
Stack<TreeNode> stack_node = new Stack<TreeNode>();
TreeNode pre_node = null;
while(root != null || !stack_node.empty()) {
while(root != null) {
stack_node.push(root);
root = root.left;
}
root = stack_node.pop();
if(pre_node != null && pre_node.val >= root.val) return false;
pre_node = root;
root = root.right;
}
return true;
}
中序遍历非递归使用了栈,时间复杂度和空间复杂度都是(O(n)),在数据结构中使用线索二叉树来构成的Morris遍历,空间复杂度只有(O(1)),因此可以使用Morris遍历。
// 5. 还可以使用morris遍历
public boolean isValidBST(TreeNode root) {
TreeNode preNode = null;
while(root != null) {
if(root.left == null) {
if(preNode != null && preNode.val >= root.val) {
return false;
}
preNode = root;
root = root.right;
}else {
TreeNode rightNode = root.left;
while(rightNode.right != null && rightNode.right != root) {
rightNode = rightNode.right;
}
if(rightNode.right == null) {
rightNode.right = root;
root = root.left;
}else {
if(preNode != null && preNode.val >= root.val) {
return false;
}
preNode = root;
rightNode.right = null;
root = root.right;
}
}
}
return true;
}
leetcode,第110题,Balanced Binary Tree,
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example:
Given the following tree [1,2,2,3,3,null,null,4,4]:
Return false.
验证平衡树,比较的就是左右子树的深度差,使用递归的话,考虑的就是回溯的时候如何往上传值,因为可能中间发现不平衡,那么传递是深度值和是否平衡,这里就是将之结合在一起。
// 速度很快,就是空间使用有点大了
public boolean isBalanced(TreeNode root) {
if(maxDepth(root) == -1) {
return false;
}
return true;
}
// 深度的简化版
private int maxDepth(TreeNode root) {
if(root == null) return 0;
int left_depth = maxDepth(root.left);
int right_depth = maxDepth(root.right);
if(left_depth == -1 || right_depth == -1 || Math.abs(left_depth - right_depth) > 1) {
return -1;
}
return Math.max(left_depth + 1, right_depth + 1);
}
总结
树的题目基本都会有递归的解法,这也是树这种结构的特性导致的,我之前整理树形的时候,会写树的各种操作,基本上都是递归写法,上面的题目也是如此,本文所有代码都会放我的github。