介绍
图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中,图是最灵活的数据结构之一,很多问题都可以使用图模型进行建模求解。例如:生态环境中不同物种的相互竞争、人与人之间的社交与关系网络、化学上用图区分结构不同但分子式相同的同分异构体、分析计算机网络的拓扑结构确定两台计算机是否可以通信、找到两个城市之间的最短路径等等。
基本要点
-
有向图:指的是一个各个节点之间的路径之间存在方向性,简而言之就是(1->2 != 2->1),这样的图称之为有向图。
-
无向图:值得是相对于有向图的一个概念,也就顶定点之间的联通没有方向可言。
-
邻接(adjacency):邻接是两个顶点之间的一种关系。如果图包含$( u , v ) $则称顶点 (v)顶点 (u)邻接。当然,在无向图中,这也意味着顶点(u)与顶点 (v)接。
-
关联(incidence):关联是边和顶点之间的关系。在有向图中,边$( u , v ) (从顶点)u(开始关联到)v(,或者相反,从)v(关联到)u$。(从后向前)。
-
路径(path):依次遍历顶点序列之间的边所形成的轨迹。注意,依次就意味着有序,先1后2和先2后1不一样。
- 简单路径:没有重复顶点的路径称为简单路径。说白了,这一趟路里没有出现绕了一圈回到同一点的情况,也就是没有环。
-
环包:含相同的顶点两次或者两次以上.
-
连通: 无向图中每一对不同的顶点之间都有路径。如果这个条件在有向图里也成立,那么就是强连通的.
- 连通分支:不连通的图是由2个或者2个以上的连通分支的并。这些不相交的连通子图称为图的连通分支。
-
有向图的连通分支:将有向图的方向忽略后,任何两个顶点之间总是存在路径,则该有向图是弱连通的,有向图的子图是强连通的,且不包含在更大的连通子图中,则可以称为图的强连通分支.下面的图中a和b是弱联通的。
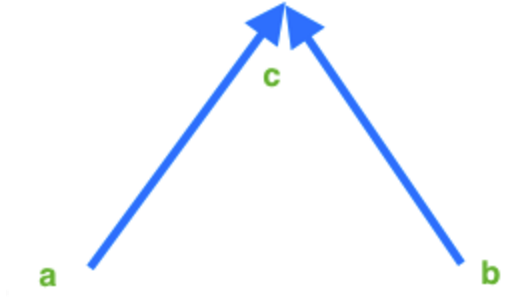
9.关节点和桥:- 关节点(割点):某些特定的顶点对于保持图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使图或者分支失去连通性,则称该顶点为关节点。
- 桥(割边):和关节点类似,删除一条边,就产生比原图更多的连通分支的子图,这条边就称为割边或者桥。
- 双连通图:不含任何关节点的图。
表示以及实现
图搜索算法
本部分完成的工作是做一些经典的题目辅助学习图论的知识,大概给一个思路代码的实现。
有向无环图(判定)
#include<iostream>
#include<malloc.h>
using namespace std;
#define maxNum 100 //定义邻接举证的最大定点数
int visited[maxNum];//通过visited数组来标记这个顶点是否被访问过,0表示未被访问,1表示被访问
int DFS_Count;//连通部件个数,用于测试无向图是否连通,DFS_Count=1表示只有一个连通部件,所以整个无向图是连通的
int pre[maxNum];
int post[maxNum];
int point;//pre和post的值
//图的邻接矩阵表示结构
typedef struct
{
char v[maxNum];//图的顶点信息
int e[maxNum][maxNum];//图的顶点信息
int vNum;//顶点个数
int eNum;//边的个数
}graph;
void createGraph(graph *g);//创建图g
void DFS(graph *g);//深度优先遍历图g
void dfs(graph *g,int i);//从顶点i开始深度优先遍历与其相邻的点
void dfs(graph *g,int i)
{
//cout<<"顶点"<<g->v[i]<<"已经被访问"<<endl;
cout<<"顶点"<<i<<"已经被访问"<<endl;
visited[i]=1;//标记顶点i被访问
pre[i]=++point;
for(int j=1;j<=g->vNum;j++)
{
if(g->e[i][j]!=0&&visited[j]==0)
dfs(g,j);
}
post[i]=++point;
}
void DFS(graph *g)
{
int i;
//初始化visited数组,表示一开始所有顶点都未被访问过
for(i=1;i<=g->vNum;i++)
{
visited[i]=0;
pre[i]=0;
post[i]=0;
}
//初始化pre和post
point=0;
//初始化连通部件数为0
DFS_Count=0;
//深度优先搜索
for(i=1;i<=g->vNum;i++)
{
if(visited[i]==0)//如果这个顶点为被访问过,则从i顶点出发进行深度优先遍历
{
DFS_Count++;//统计调用void dfs(graph *g,int i);的次数
dfs(g,i);
}
}
}
void createGraph(graph *g)//创建图g
{
cout<<"正在创建无向图..."<<endl;
cout<<"请输入顶点个数vNum:";
cin>>g->vNum;
cout<<"请输入边的个数eNum:";
cin>>g->eNum;
int i,j;
//输入顶点信息
//cout<<"请输入顶点信息:"<<endl;
//for(i=0;i<g->vNum;i++)
// cin>>g->v[i];
//初始画图g
for(i=1;i<=g->vNum;i++)
for(j=1;j<=g->vNum;j++)
g->e[i][j]=0;
//输入边的情况
cout<<"请输入边的头和尾"<<endl;
for(int k=0;k<g->eNum;k++)
{
cin>>i>>j;
g->e[i][j]=1;
g->e[j][i]=1;//无向图对称
}
}
int main()
{
graph *g;
g=(graph*)malloc(sizeof(graph));
createGraph(g);//创建图g
DFS(g);//深度优先遍历
//连通部件数,用于判断是否连通图
cout<<"连通部件数量:";
cout<<DFS_Count<<endl;
if(DFS_Count==1)
cout<<"图g是连通图"<<endl;
else if(DFS_Count>1)
cout<<"图g不是连通图"<<endl;
//各顶点的pre和post值
for(int i=1;i<=g->vNum;i++)
cout<<"顶点"<<i<<"的pre和post分别为:"<<pre[i]<<" "<<post[i]<<endl;
//cout<<endl;
//判断无向图中是否有环
if(g->eNum+DFS_Count>g->vNum)
cout<<"图g中存在环"<<endl;
else
cout<<"图g中不存在环"<<endl;
int k;
cin>>k;
return 0;
}
/*
输入:
正在创建无向图...
请输入顶点个数vNum:10
请输入边的个数eNum:9
请输入边的头和尾
1 2
1 4
2 5
2 6
4 7
5 9
6 3
7 8
9 10
*/
邻接矩阵实现拓扑排序
- 代码
#include <queue>
#include <vector>
#include <stack>
#include <iostream>
using namespace std;
enum GraphType
{
UNDIR_UNWEIGHT_GRAPH, //无向无权图
UNDIR_WEIGHT_GRAPH, //无向带权图
DIR_UNWEIGHT_GRAPH, //有向无权图
DIR_WEIGHT_GRAPH //有向带权图
};
//结点颜色代表遍历情况
enum ColorType
{
WHITE, //未访问
GRAY, //正在访问,邻接点还没访问完
BLACK //访问完毕
};
template<typename VertexType, typename InfoType>
class Graph
{
public:
Graph(int vertexNum, GraphType type) :m_vertexNum(vertexNum), m_type(type), m_arcNum(0)
{
for (int i = 0; i < MAX_VERTEX_NUM; ++i)
{
m_vertices[i].firstArc = nullptr;
}
}
void Create()
{
CreateDirUnweightGraph();
}
//输出图的信息
void Display()
{
for (int i = 0; i < m_vertexNum; ++i)
{
cout << "第" << i + 1 << "个结点为" << m_vertices[i].data << " 邻接表为:";
ArcNode* node = m_vertices[i].firstArc;
while (node)
{
cout << "->" << m_vertices[node->vertexIndex].data << "(" << node->info << ")";
node = node->next;
}
cout << endl;
}
}
//拓扑排序
void TopologicalSort()
{
cout << "拓扑排序为:";
CountInDegree();
stack<Vertex> s;
//把所有入度为0的结点入栈
for (int i = 0; i < m_vertexNum; ++i)
{
if (m_inDegreeArray[i] == 0)
s.push(m_vertices[i]);
}
int count = 0;//输出结点计数,用于判断有没有环
while (!s.empty())
{
Vertex v = s.top();
s.pop();
cout << v.data << "->";
++count;
ArcNode* node = v.firstArc;
while (node)
{
//从图中删除结点v,v指向的结点入度-1
//结点 入度为0加入栈中
if (--m_inDegreeArray[node->vertexIndex] == 0)
s.push(m_vertices[node->vertexIndex]);
node = node->next;
}
}
if (count < m_vertexNum)
cout << "图中存在环!" << endl;
}
private:
struct ArcNode
{
int vertexIndex; //该弧指向的顶点位置
struct ArcNode* next; //指向下一个弧
InfoType info; //该弧的相关信息,如权重等
};
struct Vertex
{
VertexType data; //顶点信息
ArcNode* firstArc; //指向第一条依附该节点弧的指针
ColorType color; //访问情况
};
//最大顶点数
static const int MAX_VERTEX_NUM = 20;
Vertex m_vertices[MAX_VERTEX_NUM]; //顶点列表
int m_vertexNum; //当前顶点数量
int m_arcNum; //当前弧数量
GraphType m_type; //图类型:有向无权图、有向带权图、无向无权图、无向无权图
//结点入度数组
int m_inDegreeArray[MAX_VERTEX_NUM];
private:
//初始化顶点列表
void InitVertices()
{
cout << "请输入每个顶点的关键字" << endl;
VertexType data;
for (int i = 0; i < m_vertexNum; ++i)
{
cin >> data;
m_vertices[i].data = data;
}
}
//插入一个表结点
void Insert(int headVertex, int tailVertex, InfoType info)
{
//构造一个邻接表结点,即创建一条弧
ArcNode* newNode = new ArcNode;
newNode->info = info;
newNode->next = nullptr;
newNode->vertexIndex = tailVertex;
//找到邻接表的最后一个节点
ArcNode* lastNode = m_vertices[headVertex].firstArc;
if (lastNode == nullptr)
m_vertices[headVertex].firstArc = newNode;
else
{
while (lastNode->next)
{
lastNode = lastNode->next;
}
lastNode->next = newNode;
}
++m_arcNum;
}
//创建有向无权图
void CreateDirUnweightGraph()
{
InitVertices();
cout << "请分别输入每条边的起始结点值:" << endl;
int head, tail;
while (cin >> head >> tail)
{
Insert(head, tail, 0);
}
}
void CountInDegree()
{
for (int i = 0; i < m_vertexNum; ++i)
{
m_inDegreeArray[i] = 0;
for (int j = 0; j < m_vertexNum; ++j)
{
ArcNode* node = m_vertices[j].firstArc;
while (node)
{
if (node->vertexIndex == i)
{
++m_inDegreeArray[i];
}
node = node->next;
}
}
}
}
};
int main()
{
Graph<char, int> g(6, DIR_UNWEIGHT_GRAPH);
g.Create();
g.Display();
g.TopologicalSort();
}
经典题目 Ordering_Tasks
- 代码和注释
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <memory.h>
using namespace std;
/*
拓扑的正常步骤为(方法不一定唯一):
1.从DGA图中找到一个没有前驱的顶点输出。(可以遍历,也可以用优先队列维护)
2.删除以这个点为起点的边。(它的指向的边删除,为了找到下个没有前驱的顶点)
3.重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环!
*/
int num_case, ver, num_edge;//测试样例的多少,图的顶点数和边数
int a, b;//输入的依赖关系的两个顶点
vector<int> ans;//存放最后的结果的容器
/*
优先队列,由于最终答案在可能输出的拓扑排序组合当中要求我们输出按照字典序排序的第一个答案,
那么我们是必要的对得到的答案进行处理,按照字典序排序,接着输出答案的第一个就可以了,那么字典序
是什么,实验报告里面会解释一下,这里按照字典序排列的最终结果符合数据排列升序,所以优先队列如下:
*/
priority_queue<int, vector<int>, greater<int> > Tasks;
int main() {
cin >> num_case;
while(num_case--) {
cin >> ver >> num_edge;//顶点数和边数
vector<int> task_map[ver+1];//声明动态邻接矩阵,随着问题规模的大小进行内存的申请
int indegree[ver+1];
memset(indegree,0,sizeof(indegree));//入度初始化为0
for(int i = 1; i <= num_edge; i++) {
cin >> a >> b;
indegree[b]++;//从a->b,也就是说b依赖于a,所以b的入度加一
task_map[a].push_back(b);//建图
}
for(int i = 1; i <= ver; i++) {
if(indegree[i] == 0) {
Tasks.push(i);//如果说,入度为0,放入队列
}
}
while(!Tasks.empty()) {
int temp = Tasks.top();
Tasks.pop();//从优先队列拿出来
ans.push_back(temp);//放入结果当中
vector<int>::const_iterator vec;
//当前节点的邻接节点向后搜索,每次搜索搜删除对应的边
for(vec = task_map[temp].begin(); vec != task_map[temp].end(); vec++) {
indegree[*vec]--;//删除对应的边
if(indegree[*vec] == 0) {//如果邻接节点入度为0,放到优先队列
Tasks.push(*vec);
}
}
}
for(int i = 0; i < ans.size(); i++) {
cout << ans[i] << " ";
}
cout << endl;
}
return 0;
}