还记得上学那会老师专门敲了黑板,强调方差分析很重要。。单因素方差分析(Analysis of Variance, ANOVA),如果变量多,就是多因素方差分析,还需要考虑到多重共线性,
也就是线性代数里的那些知识了。
现在写paper,基本上要用两种不同的方法做数据分析相互验证。比如用R和SPSS或者SAS,DPS之类。
但不论用什么方法,基本原理都是一样的,结果应该也一样。
首先,做方差分析的三大前提条件:
1.独立性
各样本必须是相互独立的随机样本
样本含量尽可能相等或相差不大
2.正态性
样本的总体符合正态分布,偏态分布不适用于方差分析,对偏态分布应考虑用对数转换、平方根变换、倒数变换、平方根反正弦变换等变量变换方法变为正态或接近正态分布后再进行方差分析
3.方差齐性
各组样本具有相同的方差
接下来,就比较简单了。
把数据一拷贝,再选择线性回归,选择置信区间95%,就能的出结果啦

但是如果不满足方差齐性,需要勾选上tamhane
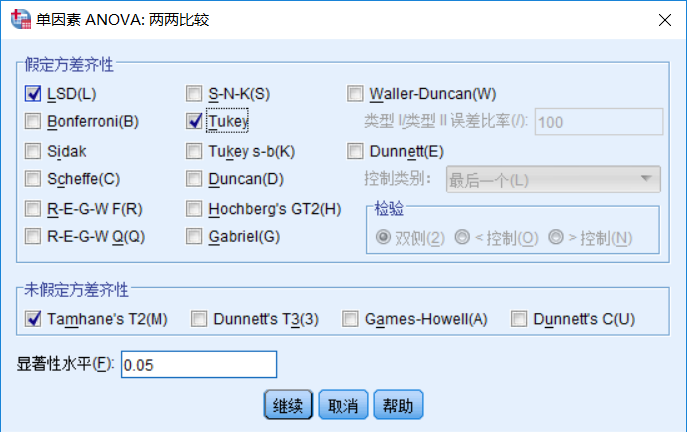
如果方差不齐,选择Tamhane选项。
2019-2-23更
又有同学问到了这个问题,方差分析和线性回归的区别
其实本质都是一样,
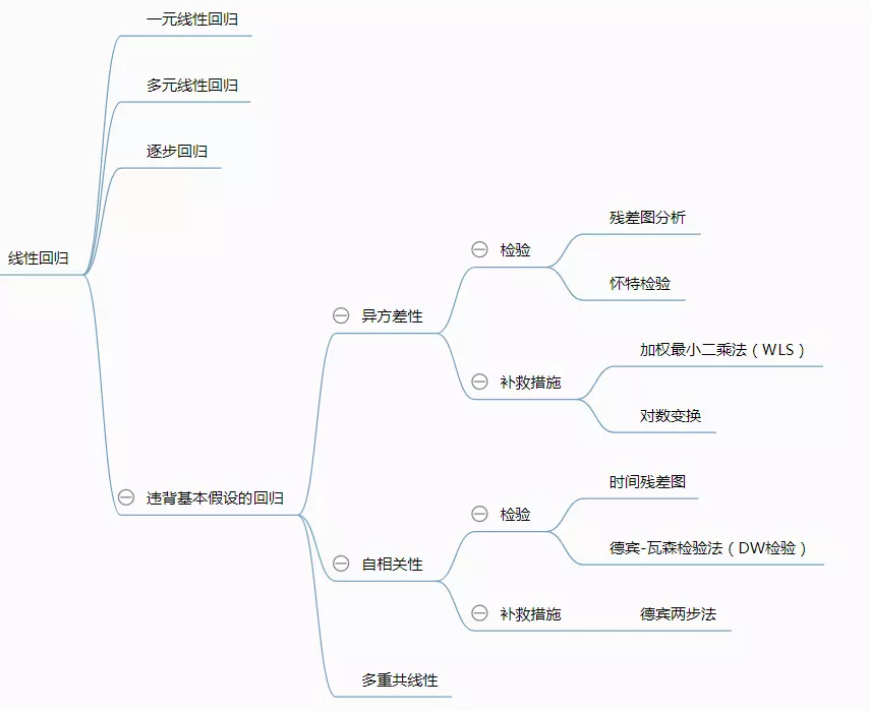
方差分析的用途,用来判定某个因素的多个水平处理对因变量的影响程度,比如说同种肥料的不同用量对作物的生长影响
见上图,通常,用于处理自变量都是离散的情形,比如性别,年份,季节,省份,当然连续变量也没问题,也可以做方差分析
核心思想是:组内方差和组间方差的比值,因为每个样本都是正态分布的话,恰好服从F分布,F分布也是个右偏分布,
假设组内差异和组件差异相等,F为1,然后求F值,也就是P值,当F值较大,P值较小时,拒绝原假设,也就是说因素显著地影响了因变量。
当自变量都是连续的,就可以直接用多元线性回归来分析了。此时,考虑到多重共线性,可以采用向前,向后逐步回归,当然一般的软件都给处理了,
同时他也做了方差分析,也就是哪个因素影响大,看P值就好了,哪个P值小,哪个因素就重要
当自变量都是连续,或者包含了离散值,但因变量是离散(二元),就用逻辑回归。逻辑回归实际上是个分类算法,另开一篇细说
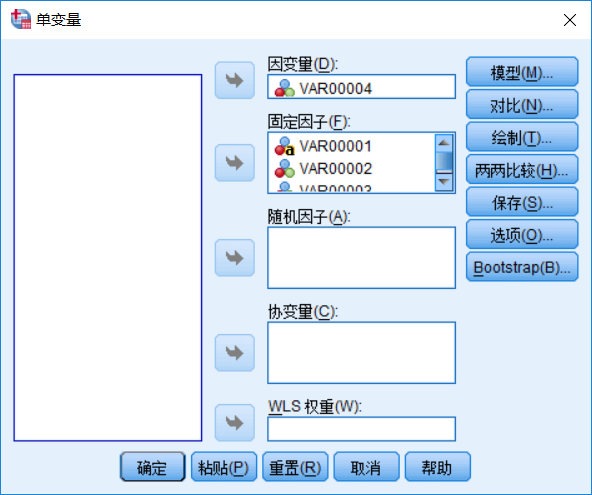
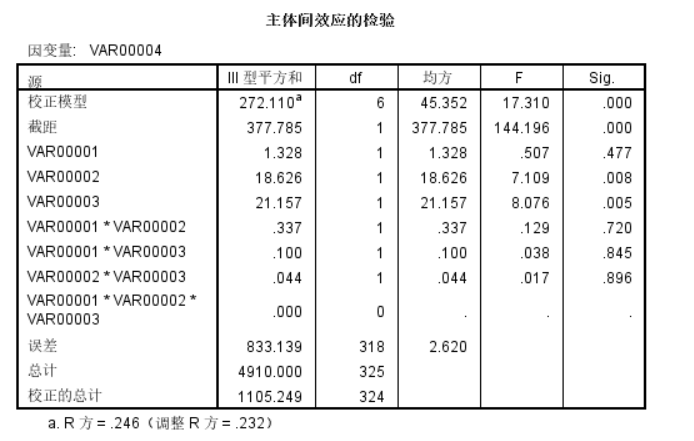
2019-4-2更新,补一下spss做多因素方差分析的流程,spss有两个地方可以处理,一个是

第一个是针对自变量来说的,单个自变量的方差分析,第二个是针对因变量来说的,单个因变量,可以有多个自变量,适合做多因素方差分析