1. 长话短说
这篇论文主要是通过设计一系列实验得到不同实验集的ID(Intrinsic Dimension),然后给出观察到的现象。这些现象也是比较符合直觉的,总结起来有这么几点:
- 数据集的ID越大,训练模型就需要越多的数据
- 数据集的extrinsic dimension对模型的训练影响不是很大,比如ImageNet图像缩放到32x32后,训练模型所需要的数据量并不会就因此减少,更多是由它本身的ID值决定的
2. Related Work
有这么一个假设,就是说子自然图像位于或者靠近 低维流行 (low-dimensional manifold)。 有两点现象能支持这个假设:
-
自然图像是locally connected,即每张图片周围都是与他本身高度相似的图像,差别可能就是亮度,对比度等特征。
-
自然图像位于 低维结构(low-dimensional structure) 上,因为图像的概率分布是高度集中的(即相似的纹理),如果我们只是对像素做均匀采样,很难得到一个有意义的图像。比如一张白色狗狗的照片,身体部位的像素绝大部分都是分布在白色区间,舌头则是高度集中在红色像素。
后续也有很多工作尝试去证明上面提到的假设。有的工作则是去尝试理解为什么深度模型能从训练集泛化到从未见过的测试集。有一类工作是从 loss landscape的角度来解释,有的则是认为 低维数据 与 不包含外在维度(extrinsic dimension)的属性 表征了分类问题的泛化难度:
- [1] 发现神经网络的特征是 low-dimensional 的
- [2] 发现神经网络不同层的特征的intrinsic dimension存在先增后降的特点
3. Intrinsic Dimension (ID) Estimation
3.1 本论文使用的ID估计方法: MLE
假设我们有一组数据点 \(\mathcal{P}\subset \mathbb{R}^N\),这些点位于或靠近低维流形 \(\mathcal{M}\subseteq \mathbb{R}^N\), 其中 \(dim( \mathcal{M} )=d<<N\)。现在的问题就是我们如何求出(或估计出) d 的大小。
一个常见的ID估计方法是找出每个样本点的 top-k 最近邻居,然后对邻居之间的距离进行建模。文献[3]中基于泊松过程使用了最大似然估计 (MLE) ,公式如下:
其中\(T_j(x)\)表示 采样点 \(x\) 到 它第j个最近邻居的欧氏距离 (norm2)。不过公式(1)是某一个样本点的结果,所有后面有算法[4]做出了修正,即取多个 (n) 样本点ID估计值的均值
基于MLE估计得到ID值有两个需要注意的问题:
- 如公式(2)所示,估计值依赖于 k 的取值
- 除了局部均匀性假设外,MLE还假设数据产生于一连串的独立随机变量,这些变量可以写成具有平滑密度的连续和足够平滑的随机变量的函数,但是对于自然图像数据集来说,这个假设我们很难判断真假。
3.2 一些其他ID估计的方法
- [5] GeoMLE 利用基于不同大小邻居数量 (即 k) 的近邻距离 对 标准MLE进行多项式回归 来说明密度的非均匀性和流形的非线性。问题在于它的ID值是 多个样本 \(\hat{m}_{k}(x)\) 的平均,而公式(2) 中是对 \(\hat{m}_{k}(x)^{-1}\) 求平均后,再取倒数得到最终的估计值。文章也明确说[5] 的估计值非常不准。下图是GeoMLE在 d-dimensional Hypercube data上的表现结果。
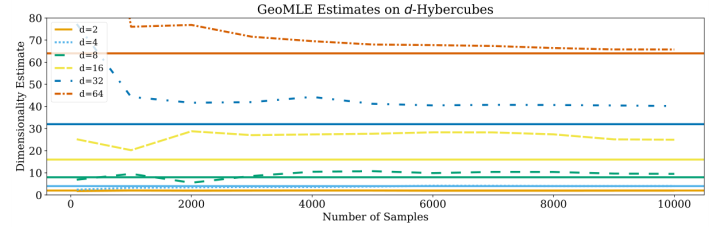
-
[6] 提出了 TwoNN 算法来估计ID值,简单说就是他基于两个邻居之间的距离 (即 k=2 )来估计ID。 文献[2]就是基于这个算法的。
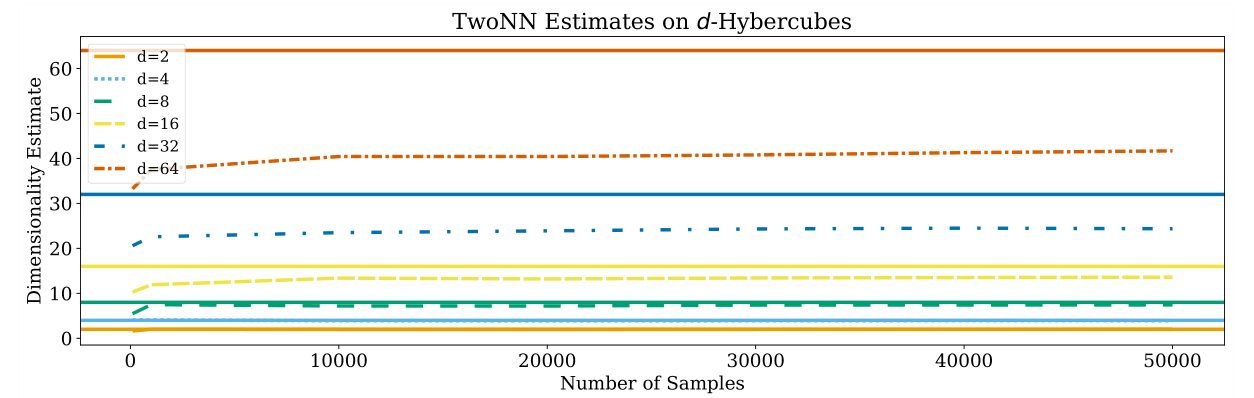
-
这篇文章不同邻居之间的距离是使用 norm2 的欧氏距离计算的,而 [7] 中使用的是 geodesic distance,记为 kNN graph distance。
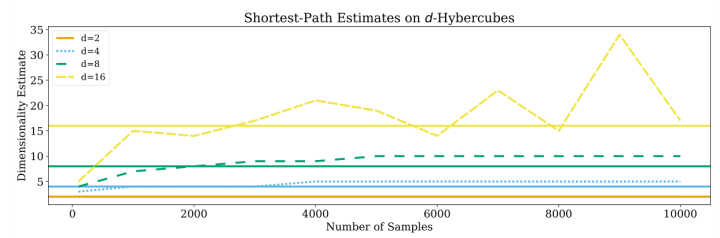
上面3个图可以看到GeoMLE和TwoNN的估计值一般会比真实值要打,即overestimate。而KNN graph则是略微地underestimate。不同估计方法对不同数据集的ID估计结果如下。TwoNN对MNIST的ID估计值比CIFAR-10还高,这可能多少和直觉相违背。另外前三个数据集对CIFAR10的ID估计值都要比CIFAR100高,这个感觉也有点反直觉。
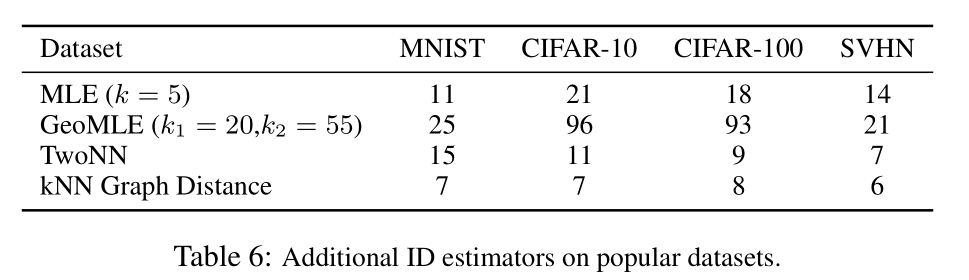
4. 在合成数据上验证 Intrinsic Dimension
4.1 直观感受ID对图像分类的影响
作者用BigGAN做了个实验。BigGAN有 128个latent entries,输出大小为128x128x3的图像。作者将128个latent entries大多数设置为0,只留下 \(\bar{d}\) 个free entries,即视为intrinsic dimension。然后给出了不同 \(\bar{d}\) 设置下一个类别(即 basenji)生成的图像的对比,如下图示。可以看到 ID值越小,生成的图片背景越简单,当 \(\bar{d}=128\) 时,背景复杂了很多。其实换个角度想,当数据的ID越小的时候则表示该数据越容易被区分。文献[2]的实验对比了resent18/50/152等就发现网络最后一层的ID值越低,模型最终的acc也相对高一些。

作者还在 \(\bar{d}=10\) 的情况下比较了不同 k 的取值对最终ID估计的影响,结果如下。我们可以看到如下几个现象:
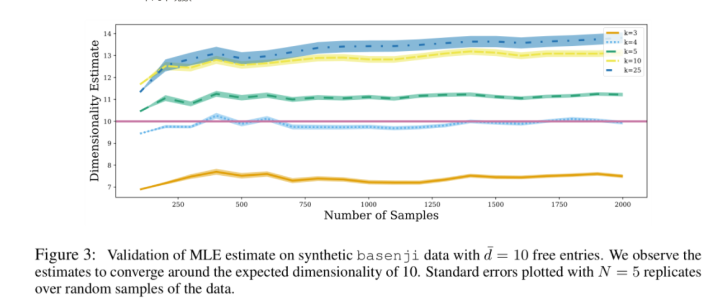
- 纵坐标10代表ground truth,当k=4的时候得到的ID估计值非常接近真实值。
- 原本的latent维度是128,虽然其他k值有一定误差,但是整体上偏差不是很大,他们都很接近10
- ID的估计比较robust,可以看到即使把采样点数量从125增加到2000后,不同k得到的ID的预测值都是相对稳定的。这表明我们可以只使用一部分数据就能很好地得到ID估计值。
4.2 两个假设
作者还进一步在合成数据集上设计了实验来验证两个假设:
- ID低的数据的sample complexity要小于 ID高的数据
为了验证这个,作者选择了basenji和beagle这两类图像来用BigGAN来生成4组不同的数据集,主要区别是intrinsic dimension的不同,具体设置如下:
- intrinsic dimension是指latent size,四个数据集对应的大小分别是16,32,64,128
- extrinsic dimension是指最终生成的图像大小,四个数据集都是一样的,即 3x32x32
数据集生成好后,作者使用ResNet-18 在这4个数据集上去训练,实验结果如下。可以看到ID (即latent size)越小的数据集,训练ResNet-18所需的训练样本数量也就越少。实验结果证明了假设。
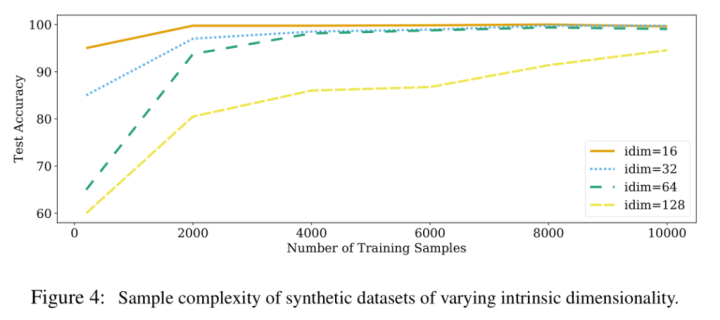
- extrinsic dimension和sample complexity没有关系
为了验证第二个假设,作者这次固定intrinsic,改变extrinsic dimension,也生成了4个不同的数据集,具体设置如下:
- intrinsic dimension: latent size都固定位128
- extrinsic dimension:生成图像的大小分别是16, 32, 64, 128, 256
实验结果如下图,可以看到此时4个数据集在使用2000个训练样本后基本就能达到相似的分类准确率了。实验结果表明extrinsic dimension对sample complexity的影响很小。
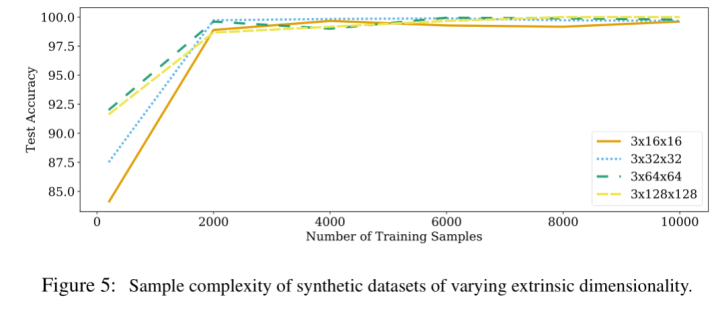
5. 在真实数据集上验证 Intrinsic Dimension
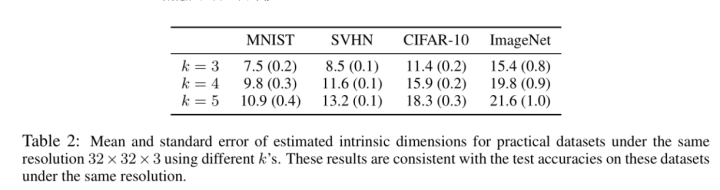
前面都是在GAN生成的数据集上做的实验,作者还在像MNIST,CIFAR-10等真实数据集上也做了验证试验。下图是在原始数据集上使用MLE得到的在不同 k 大小下的 ID 估计值。可以看到估计的结果符合预期,即数据集越难,ID值越大。
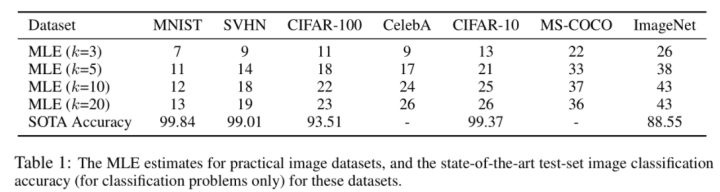
因为每个数据集的图形大小不一样,所以不同数据集的图像大小都缩放到 32x32 以保证extrinsic dimension都一样。实验设置和上面的合成数据集的设置类似,比如在ImageNet上随机选取两个类别的数据构造成一个二分类数据子集,然后计算出 ID 值。Table 2是基于两个类别得到的ID值,Table 1是基于原始数据集得到的ID值,可以看到二者虽然具体的ID值不同牡丹石整体呈现的趋势是类似的,即数据集越难,ID值越大。
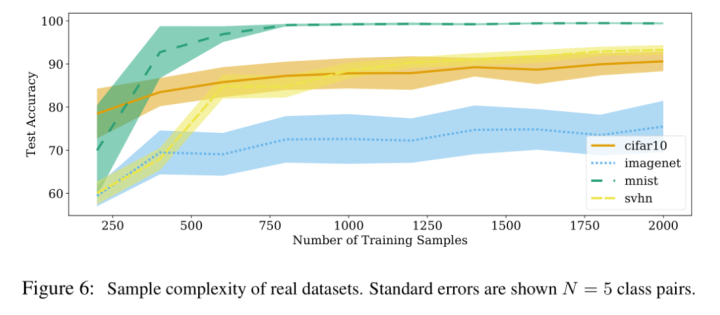
下图是在4个真实数据集上的结果,每个数据集跑了5次,每次选取不同的两个类别组成subnet。可以看到在真实数据集上的结果和Figure 4的结果类似,intrinsic dimension大的数据集(如ImageNet)需要采样更多的训练样本。
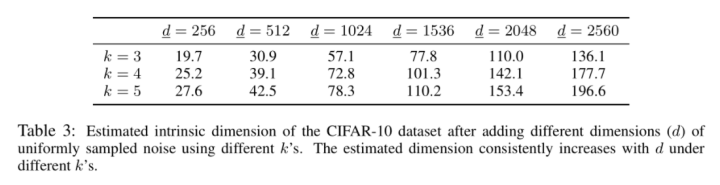
作者还做了一个比较有意思的实验,就是给数据集加上噪声。其实像ImageNet本身真实的ID我们是不知道的,但是噪声数据的ID我们是可以控制的,所以假如我们构造一个ID为 \(\underline{d}\) 的噪声并把它加到原图像上去,那么得到的新的图像的ID肯定是大于或等于\(\underline{d}\)的。Table 3 给出了加上不同ID噪声后,CIFAR-10数据集的ID估计值的变化情况。可以看到加上噪声后数据集的ID似乎并没有达到噪声的ID值,这很可能是因为数据点太少导致的。不过可以看到的是加入噪声的ID值越大,得到的新的数据集自身的ID值也是随之增加的。
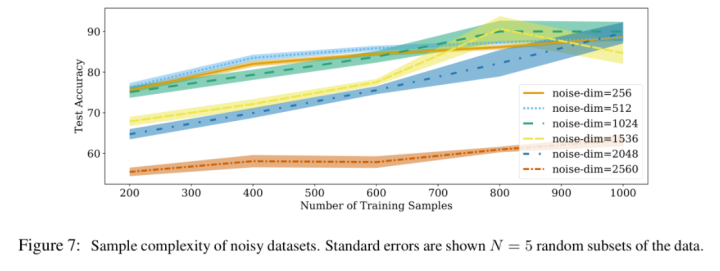
基于加入噪声后的数据集,作者也做了sample complexity实验的比较,实验现象和前面的类似。
Reference
[1] Sixue Gong, Vishnu Naresh Boddeti, and Anil K Jain. On the intrinsic dimensionality of image representations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3987–3996, 2019.
[2] Alessio Ansuini, Alessandro Laio, Jakob H Macke, and Davide Zoccolan. Intrinsic dimension of data representations in deep neural networks. In Advances in Neural Information Processing Systems, pp. 6111–6122, 2019.
[3] Elizaveta Levina and Peter J Bickel. Maximum likelihood estimation of intrinsic dimension. In Advances in neural information processing systems, pp. 777–784, 2005.
[4] David J.C. MacKay and Zoubin Ghahramani. Comments on ‘Maximum Likelihood Estimation of Intrinsic Dimension’ by E. Levina and P. Bickel (2004), 2005. URL http://www.inference.org.uk/mackay/dimension/.
[5] Marina Gomtsyan, Nikita Mokrov, Maxim Panov, and Yury Yanovich. Geometry-aware maximum likelihood estimation of intrinsic dimension. In Asian Conference on Machine Learning, pp. 1126–1141, 2019.
[6] Elena Facco, Maria d’Errico, Alex Rodriguez, and Alessandro Laio. Estimating the intrinsic dimension of datasets by a minimal neighborhood information. Scientific Reports, 7(1):12140, 2017.
[7] Daniele Granata and Vincenzo Carnevale. Accurate estimation of the intrinsic dimension using graph distances: Unraveling the geometric complexity of datasets. Scientific reports, 6:31377, 2016.