本文笔记参考Wang Shusen老师的课程:https://www.youtube.com/watch?v=aButdUV0dxI&list=PLvOO0btloRntpSWSxFbwPIjIum3Ub4GSC&index=1
1. 回顾Attention
在介绍Transformer之前,我们首先回顾一下Attention机制。我们要知道Attention的提出的目的是为了解决句子太长而出现的遗忘问题。
而要解决遗忘问题,一个很自然的想法就是我复习一下前面的单词,即我需要计算当前位置和前面输入的数据的关系。
1.1 Hidden state
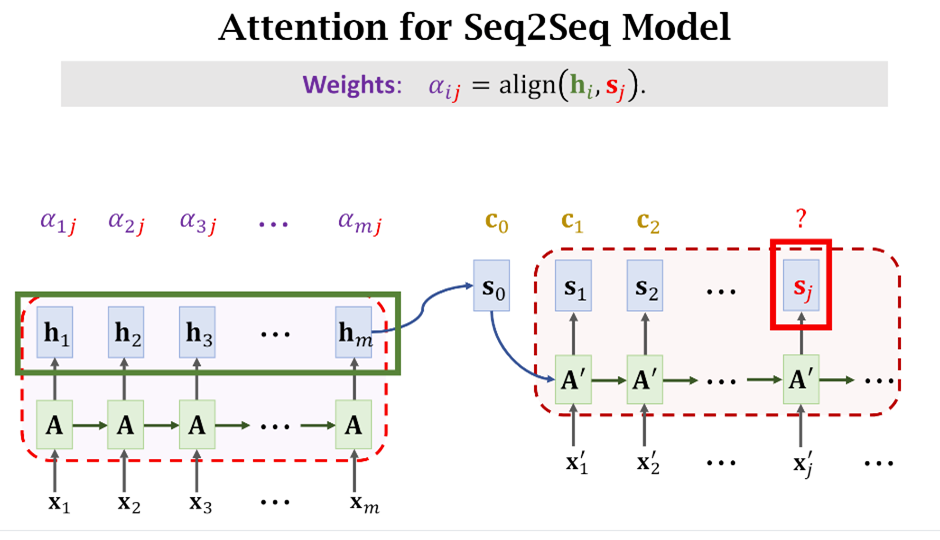
对应到上图,隐状态(s_j)计算公式如下,
1.2 Context Vector
虽然看起来(s_j)只依赖于上一时刻(单词)的结果,其实其中的Context vector (c_{j-1}) 已经包含了前面单词的信息。以(c_j)的计算为例:
上面公式中的(align)可以有不同的计算方式,它计算的是(h_i)和(s_j)的关系。注意,我们需要计算(s_j)与左边所有({h_i,iin[1,m]})的关系,得到对应的权重({alpha_{ij},iin[1,m]}),最后把所有的({h_i,iin[1,m]})加权求和就得到了第(j)个预测单词的特征和原句子每个单词之间的关系。
1.3 Q,K,V
上一节中(alpha_{ij})要通过计算(h_i)和(s_j)之间的关系得到,一个最简单的办法就是把这两个矩阵直接相乘,但是这样一来可能会有问题:一是两个矩阵可能形状不匹配,没法直接做矩阵乘法;二是直接相乘可能并不能求出二者之间的关系。所以很自然地我们给这两个矩阵分别左乘一个矩阵(W_k)和(W_Q),这两个矩阵的参数都是可学习的。
为了方便理解,下图仅以计算(align(h_i,s_j))为例。

在实际计算的时候不会像上图一样,一个一个地去算,而是以矩阵相乘的形式计算。比如把m个(h_i)合并成一个大矩阵(Hinmathbb{R}^{emb imes m}),它会被左乘一个矩阵(W_Kin mathbb{R}^{j imes emb}),得到(K=W_KHinmathbb{R}^{j imes m})。同理右边所有的(s)拼接成大矩阵(Sinmathbb{R}^{emb imes j}),然后左乘(W_Qin mathbb{R}^{j imes emb}),得到(Q=W_QSinmathbb{R}^{j imes j}),其中(emb)表示每个词向量映射成隐状态矢量的长度,即(h_iin mathbb{R}^{emb imes 1})。
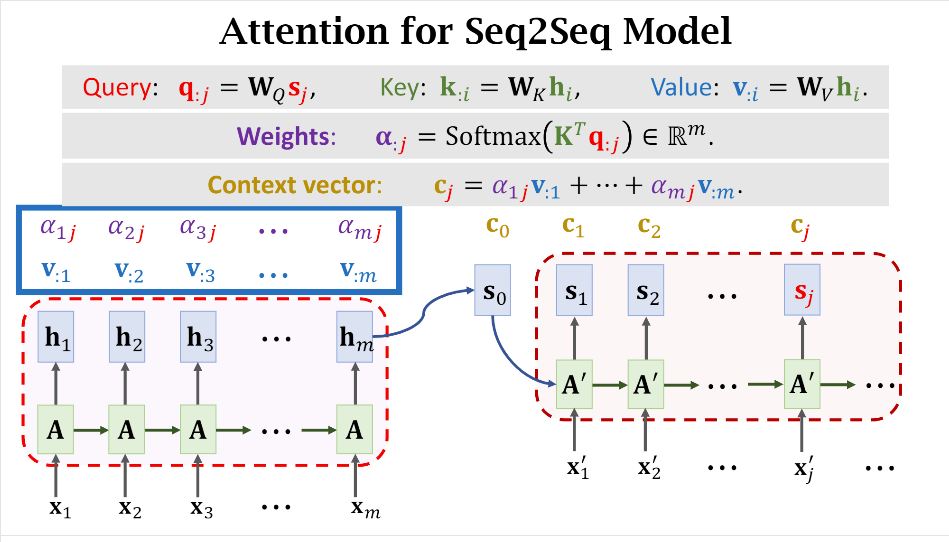
有了(q,k),就可以计算出权重(alpha),其实按照1.2节中的公式就能计算出(c)了,只不过这里将(h)进一步做了映射,替换成了(v)。
这也就解释了Transformer的Attention机制中Q,K,V三个矩阵的来源了。下图给出了完整的用于SequenceToSequence的注意力机制计算示意图。
2. Attention without RNN
终于回顾完了Attention的计算逻辑,下面我们探讨一下如果去除RNN,只保留Attention模块。
2.1 Attention Layer
下面我们一步一步看如何构造没有RNN的Attention Layer。
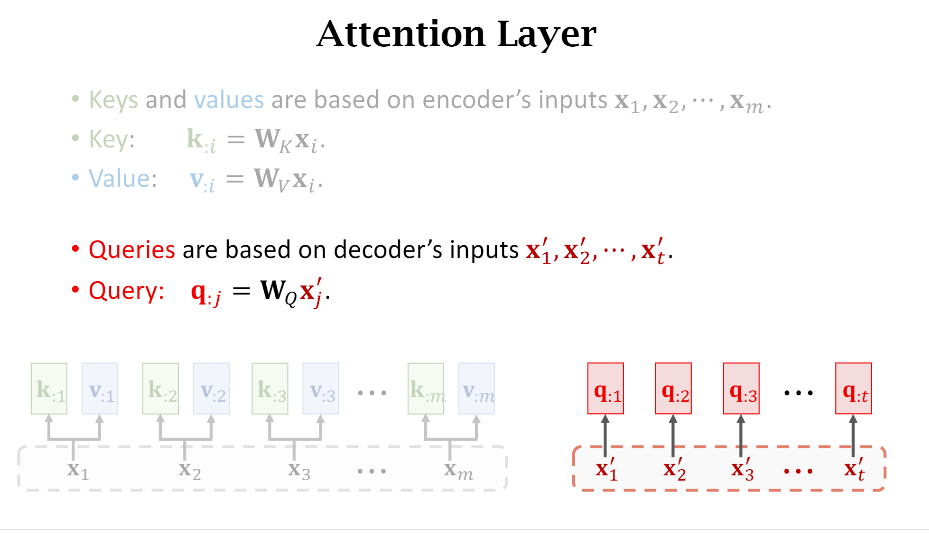
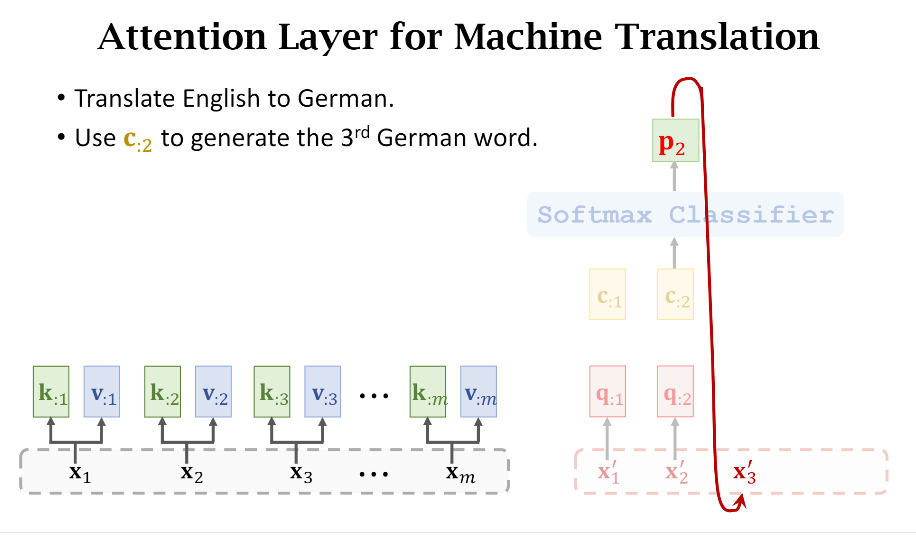
- Encoder和Decoder的输入
可以看到Encoder和Decoder的输入长度是不一样的,这也可以理解,在做汉英翻译任务的时候,两种语言的单词数通常是不一样的。(x_1)表示原句子的第一个词的embedding,通常是一个一维向量。

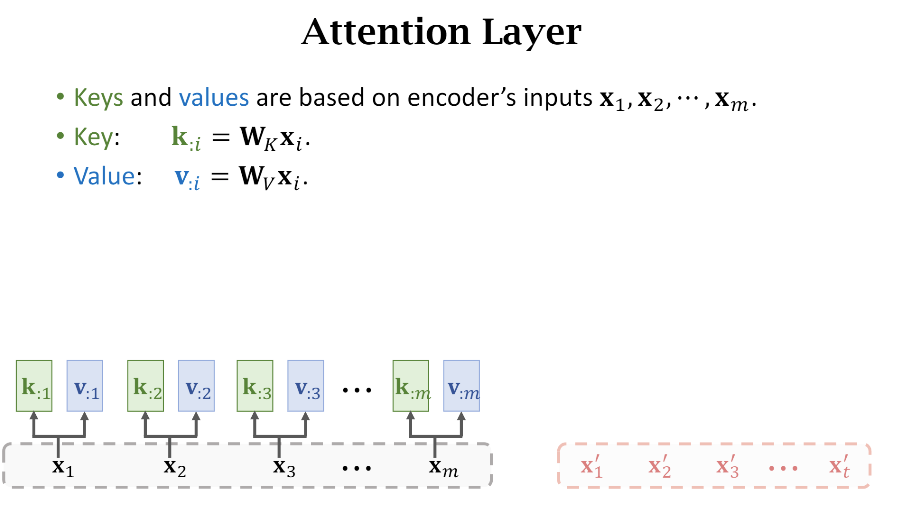
- Keys和Values
我们根据第一节可以知道接下来需要计算原句子每个词的Key和Value,
- Queries
下一步我们计算Decoder每个输入词的Query。
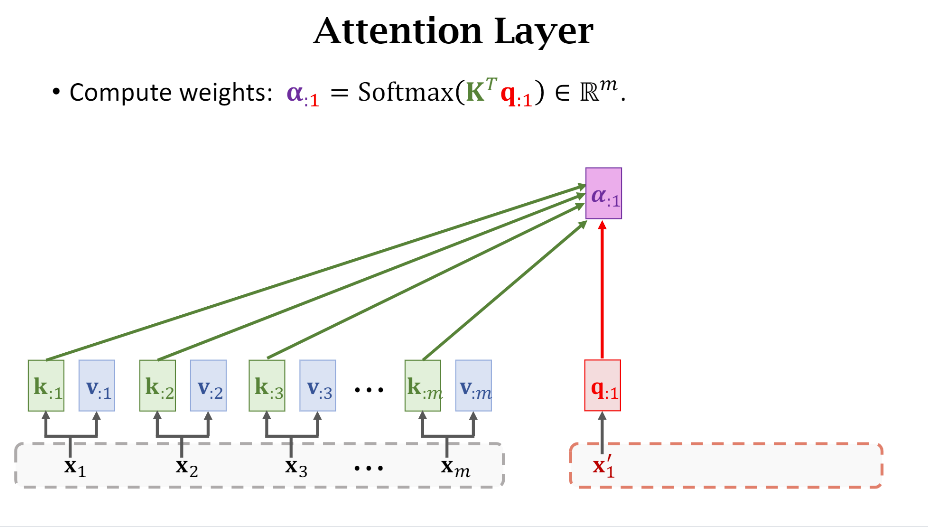
- 计算权重(alpha)
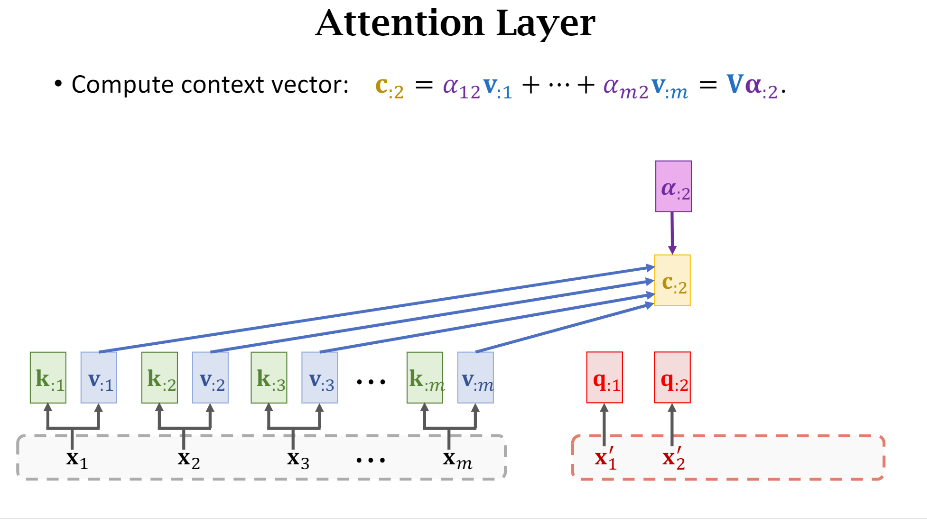
- 计算Context Vector
可以看到权重的计算用的是Key和Query之间的关系。
其实仔细想想Key,Value,Query这些词的命名还挺有意思的,比如Query就好像是我发起了一次请求,我要计算当前这个词和原句子中所有词的关系,然后原句子中每个词都有一个被唯一编码的Key,通过计算Query和Key的关系就得到了彼此之间的权重关系。
有了权重关系之后,我把原句子中所有词的值(Value)乘上对应的权重(Weights),然后累加不就得到了当前这个词和原句子的上下文(Context)关系嘛,所以简写成字母c。
以此类推,我们可以计算出Decoder所有词对应的Query((q))和Context((c))
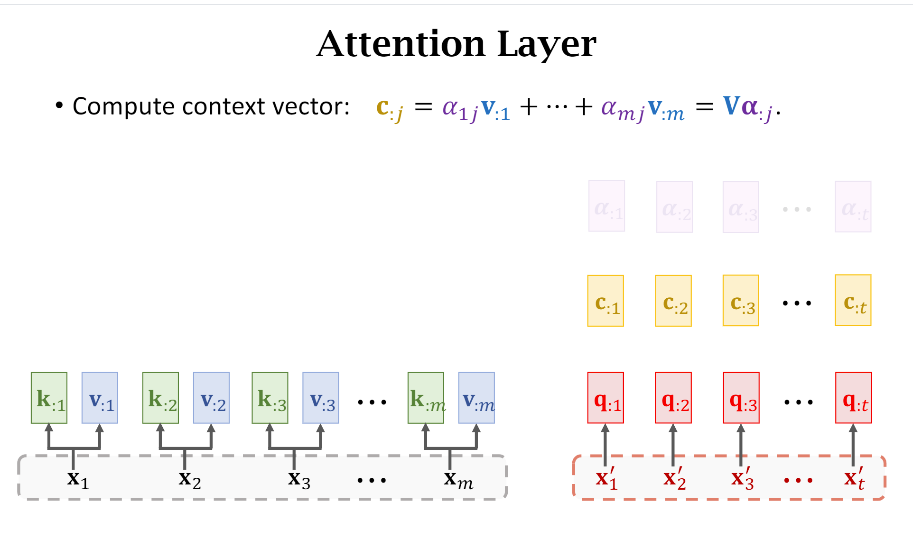
有一个需要注意的地方是Decoder的输入是依赖于上一时刻的预测,比如第2个词(x_2')通过计算得到了(c_{:2}),之后会被喂给一个Softmax分类器得到一个词分布(p_2),简单理解就是类似于分类任务,每个词会有不同的置信度,假如我们选择置信度最高的词,然后该词就会作为下一次输入,即(x_3')。
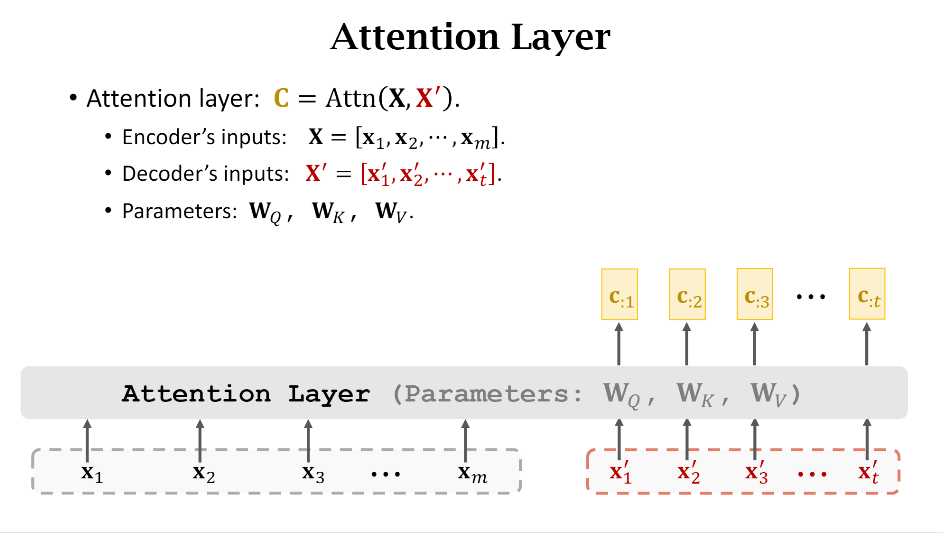
最后为了方面绘图,上面一系列复杂的操作(Q,K,V)就被简化成了下图:
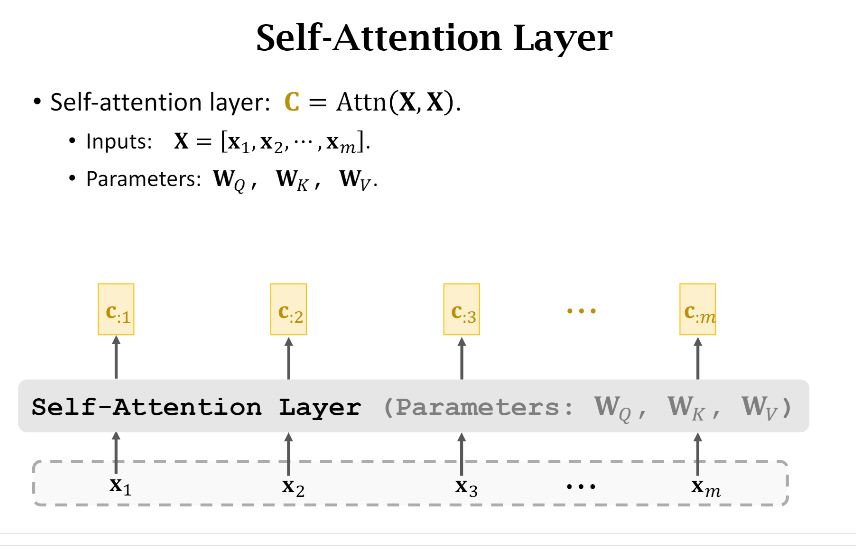
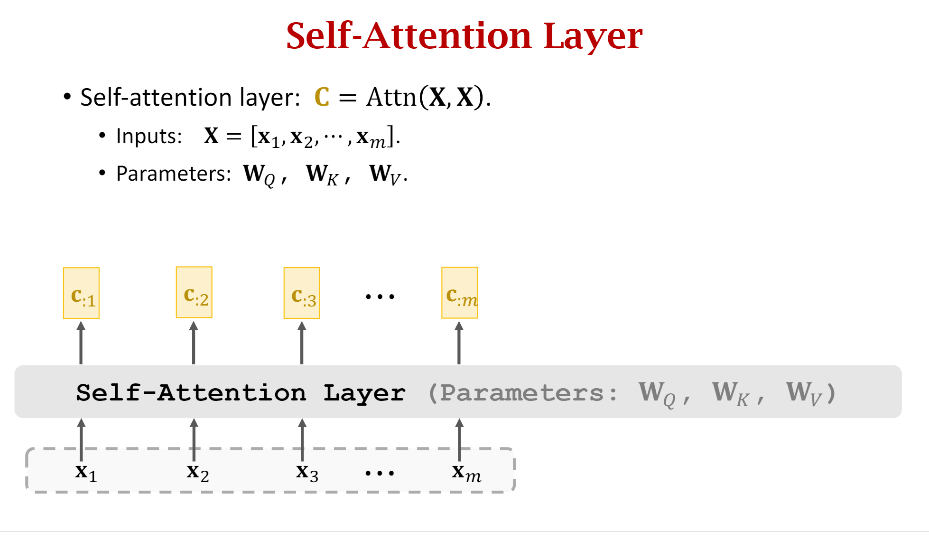
3. Self-Attention without RNN
上面Attention without RNN是以Encoder和Decoder为例进行介绍的,那么Self-Attention without RNN就很好理解了。你可以和上一个图片仔细对比一下区别,你会发现Self-Attention其实就是自己和自己做Attention运算。
和第二节一样,我们还是一步一步地去看看Self-attention到底是怎么计算的。
- Inputs
此时只有一个输入句子,由m个单词组成
- Q,K,V计算
因为是Self-attention,所以我们一步到位计算出每个单词的q,k,v向量
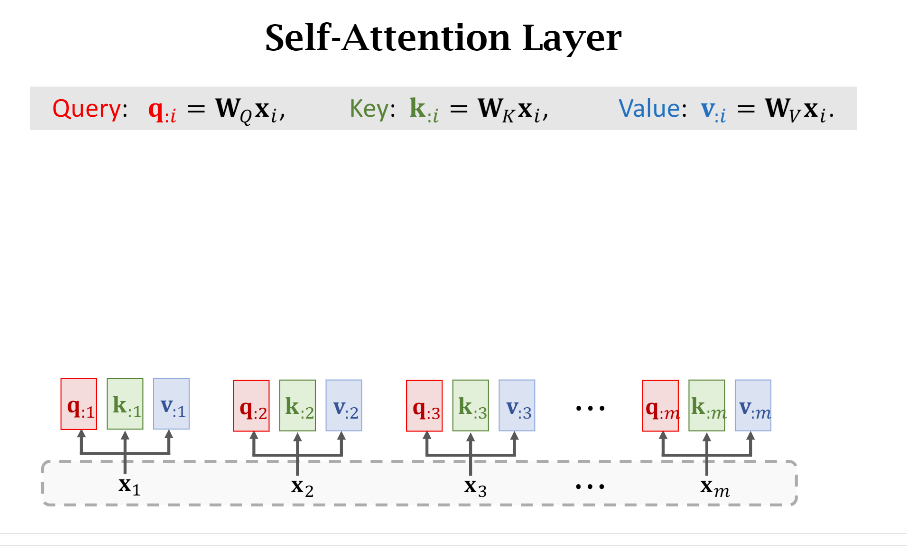
- 权重
如果要计算第(i)个单词和其他单词之间的权重,就只需要拿第(i)个单词的Query(q_{:i})和所有单词的Key({k_{:,j},jin[1,m]})进行计算。
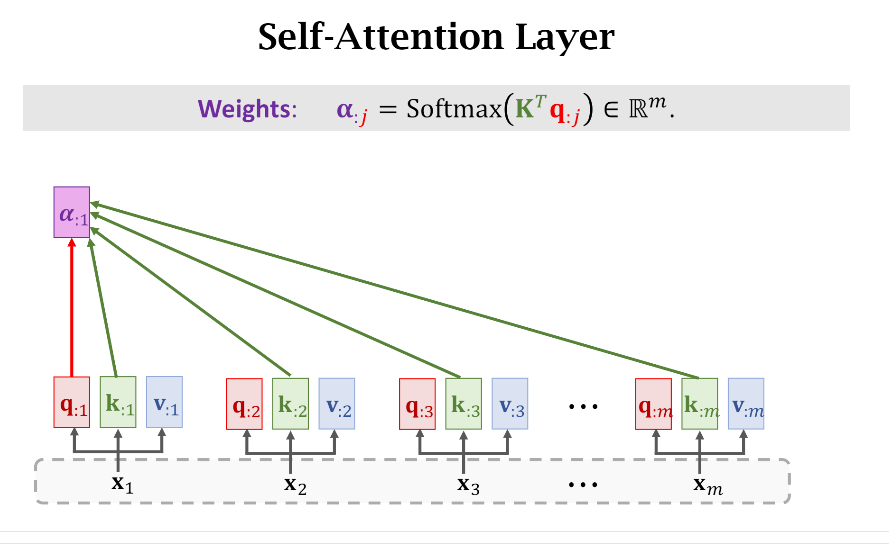
在真实代码实现的时候,其实就是(Softmax(K^TQ))就完事了,得到如下图的结果
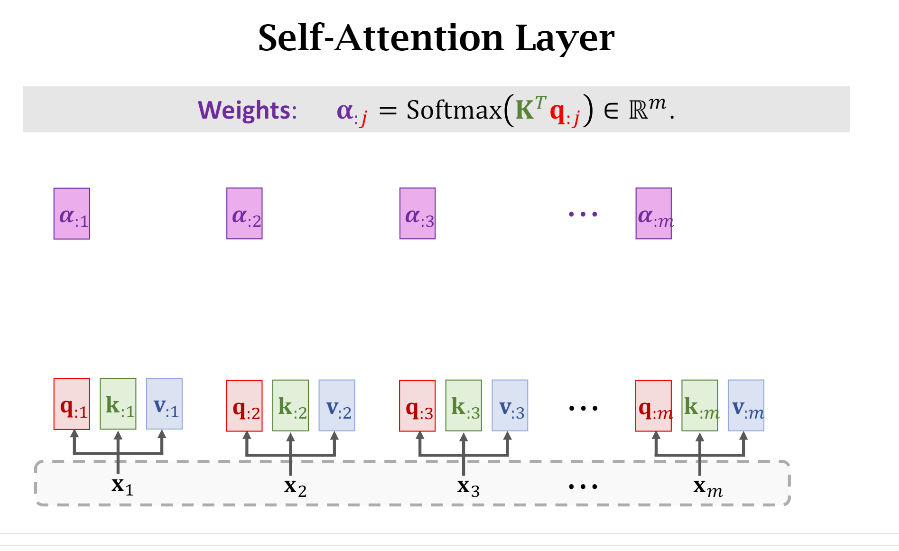
- Context
接下来咱们按部就班地拿Weight和Value计算Context Vector(或者说Context Matrix)
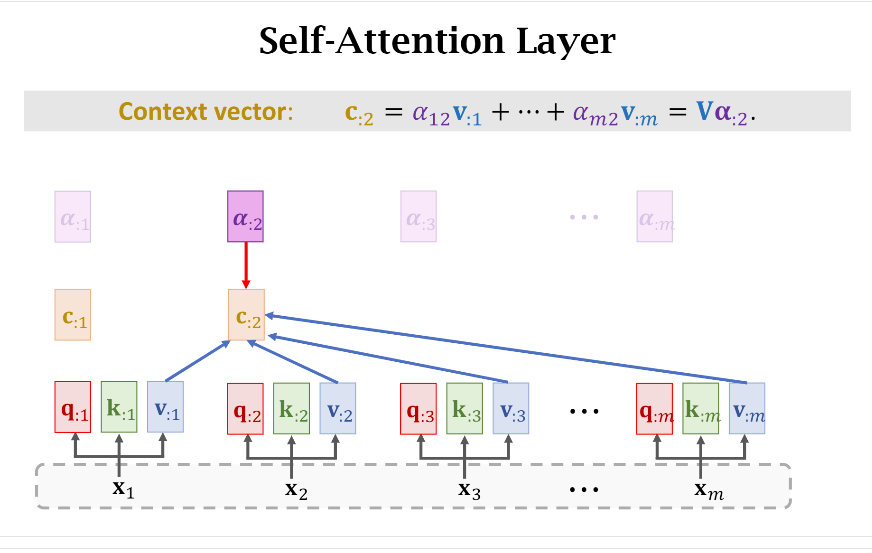
同理,在真实代码层面,也是直接计算(V cdot Softmax(K^TQ))就可以得到所有的({c_{:j},jin[1,m]})
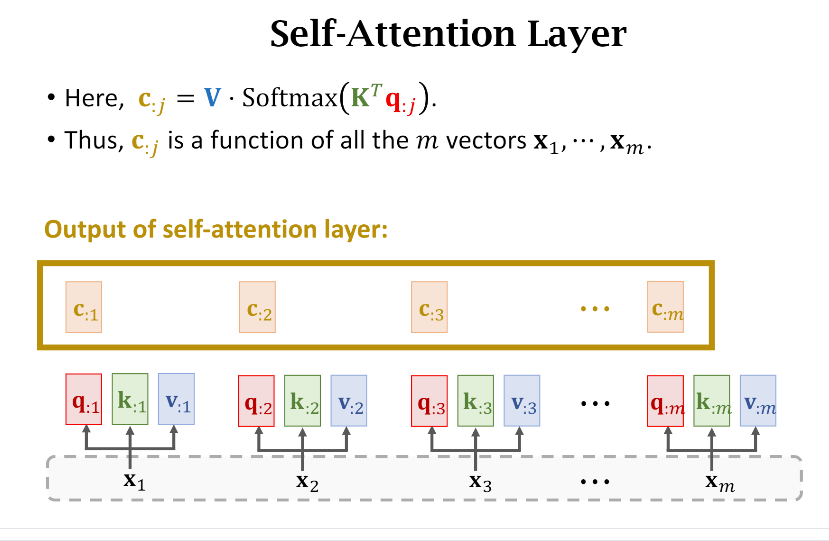
同样,我们把Self-attention层简化成下图