Matlab图论工具箱的命令见表1
表1 matlab图论工具箱的相关命令
|
命令名 |
功能 |
|
graphallshortestpaths |
求图中所有顶点对之间的最短距离 |
|
graphconncomp |
找无向图的连通分支,或有向图的强弱连通分支 |
|
graphisdag |
测试有向图是否含有圈,不含圈返回1,否则返回0 |
|
graphisomorphism |
确定两个图是否同构,同构返回1,否则返回0 |
|
graphisspantree |
确定一个图是否是生成树,是返回1,否则返回0 |
|
graphmaxflow |
计算有向图的最大流 |
|
graphminspantree |
在图中找最小生成树 |
|
graphpred2path |
把前驱顶点序列变成路径的顶点序列 |
|
graphshortestpath |
求图中指定的一对顶点间的最短距离和最短路径 |
|
graphtopootder |
执行有向无圈图的拓扑排序 |
|
graphtraverse |
求从一顶点出发,所能遍历图中的顶点 |
1.图的最短路径graphallshortestpaths函数的命令格式:
[dist]=graphallshortestpaths(G)
[dist]=graphallshortestpaths(G,...’Directed’,DirectedValue,...)
[dist]=graphallshortestpaths(G,...’Weights’,WeightsValue,...)
G是代表一个图的N*N稀疏矩阵,矩阵中的非零值代表一条边的权值:DirectedValue属性表示图是否为有向图,false代表无向图,true代表有向图,默认为true。WeightsValue是矩阵G中边的自定义权值列向量,该属性可以使我们使用零权值。输出[dist]是一个N*N的矩阵,每一个元素代表两点之间最短距离,对角线上的元素总为零,不在对角线上的零表示起点和终点的距离为零,inf值表示没有路径。
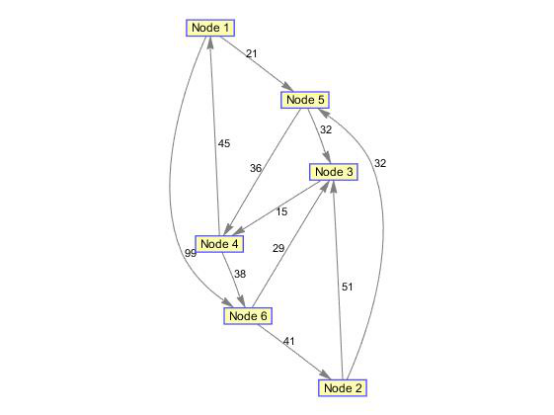
(1)创建并显示一个含有6个结点11条边的有向图
w=[41 99 51 32 15 45 38 32 36 29 21];%权值向量 dg=sparse([6 1 2 2 3 4 4 5 5 6 1],[2 6 3 5 4 1 6 3 4 3 5],w)%构造的稀疏矩阵表示图 h=view(biograph(dg,[],'ShowWeights','on'))%显示图的结构 dist=graphallshortestpaths(dg)%显示图中每对结点之间的最短路径
dist =
0 136 53 57 21 95
111 0 51 66 32 104
60 94 0 15 81 53
45 79 67 0 66 38
81 115 32 36 0 74
89 41 29 44 73 0
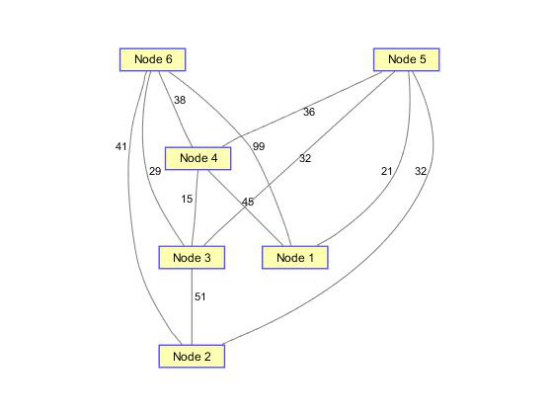
(2)创建无向图,结点信息同上
ug=tril(dg+dg');%要求生成的无向图是一个下三角矩阵 view(biograph(ug,[],'ShowArrows','off','ShowWeights','on')); dist=graphallshortestpaths(ug,'directed',false)
dist =
0 53 53 45 21 82
53 0 51 66 32 41
53 51 0 15 32 29
45 66 15 0 36 38
21 32 32 36 0 61
82 41 29 38 61 0
2.最小生成树graphminspantree函数的调用格式:
[Tree,pred]=graphminspantree(G)
[Tree,pred]=graphminspantree(G,R)
[Tree,pred]=graphminspantree(...,’Method’,MethofValue,...)
[Tree,pred]=graphminspantree(...,’Weights’,WeightsValue,...)
该函数用来寻找一个无循环的节点集合,连接无详图的全部节点,并且总的权值最小。Tree是一个代表生成树的稀疏矩阵,pred是包含最小生成的祖先节点的向量。G是无向图,R代表根节点,取值为1到节点数目,Method可以选择‘Kruskal’,’Prim’算法。
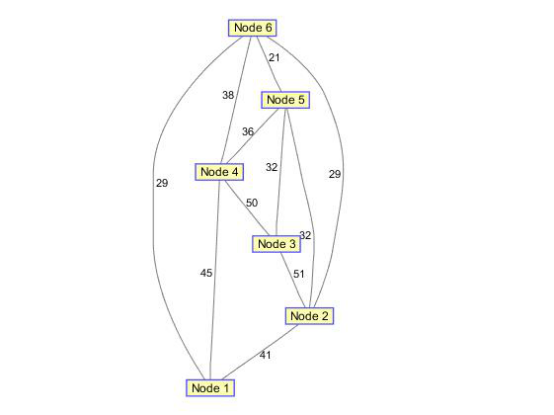
(1)构造无向图
w=[ 41 29 51 32 50 45 38 32 36 29 21]; dg=sparse([1 1 2 2 3 4 4 5 5 6 6],[2 6 3 5 4 1 6 3 4 2 5],w) ug=tril(dg+dg'); view(biograph(ug,[],'ShowArrows','off','ShowWeights','on'));
[st,pred]=graphminspantree(ug)%生成最小生成树 h=view(biograph(st,[],'ShowArrows','off','ShowWeights','on')); Edges=getedgesbynodeid(h);%提取无向图h的边集 set(Edges,'LineColor',[0 0 0]);%设置颜色属性 set(Edges,'LineWidth',1.5)%设置边值属性

3.计算有向图的最大流graphmaxflow,函数格式为:
[MaxFlow,FlowMatrix,Cut]=graphmaxflow(G,SNode,TNode)
[...]=graphmaxflow(G,SNode,TNode,...’Capacity’,CapacityValue,...)
[...]=graphmaxflow(G,SNode,TNode,...’Method’,MethodValue,...)
G是N*N的稀疏矩阵,表示有向图,SNode和TNode都是G中的节点,分别表示起点和目标点,CapacityValue为每条边自定义容量的列向量;MethodValue可以取‘Edmonds’和‘Goldberg’算法。输出MaxFlow表示最大流,FlowMatrix是表示每条边数据流值的稀疏矩阵,Cut表示连接SNode到TNode的逻辑向量,如果有多个解时,Cut是一个矩阵。
(1)构造带有节点和边的有向图
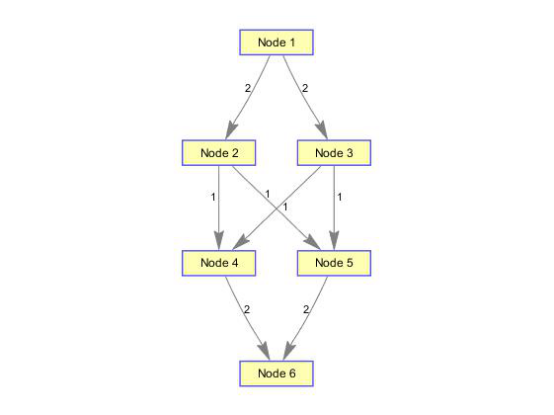
cm=sparse([1 1 2 2 3 3 4 5],[2 3 4 5 4 5 6 6],[2 3 3 1 1 1 2 3 ],6,6); %6个节点8条边 [M,F,K]=graphmaxflow(cm,1,6);%计算第1个到第6个节点的最大流 h=view(biograph(cm,[],'ShowWeights','on'));%显示原始有向图的图结构
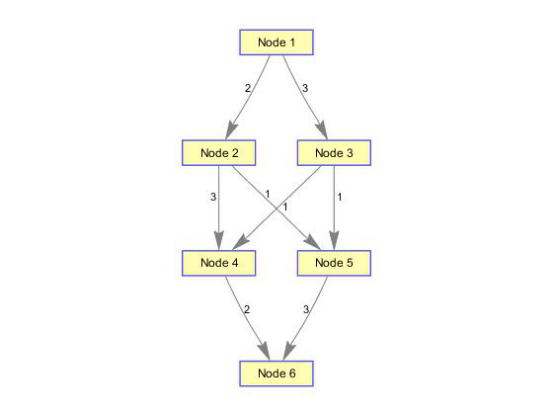
h1=view(biograph(F,[],'ShowWeights','on'));%显示计算最大流矩阵的图结构
4.图的遍历函数graphtraverse,命令格式如下:
[disc,pred,closed]=graphtraverse(G,S)
[...]=graphtraverse(G,S,...’Directed’,DirectedValue,...)
[...]=graphtraverse(G,S,...’Depth’,DepthValue,...)
[...]=graphtraverse(G,S,...’Method’,MethodValue,...)
G是有向图,S为起始节点,disc是节点索引向量,pred是祖先节点索引向量
(1)创建一个有向图
DG=sparse([1 2 3 4 5 5 5 6 7 8 8 9],[2 4 1 5 3 6 7 9 8 1 10 2],true,10,10) h1=view(biograph(DG));
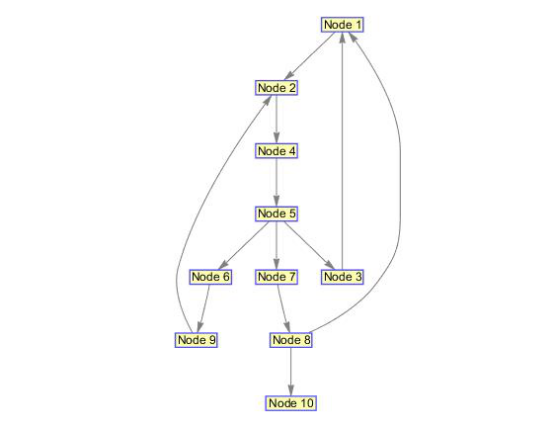
order=graphtraverse(DG,4)%使用深度优先算法从第4个节点开始遍历 order2=graphtraverse(DG,4,'Method','BFS')%使用广度优先遍历 index=graphtraverse(DG,4,'depth',2)%标记与节点4邻近的深度为2的节点
order =
4 5 3 1 2 6 9 7 8 10
order2 =
4 5 3 6 7 1 9 8 2 10
index =
4 5 3 6 7