1631. Path With Minimum Effort (M)

Path With Minimum Effort (M)

题目

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

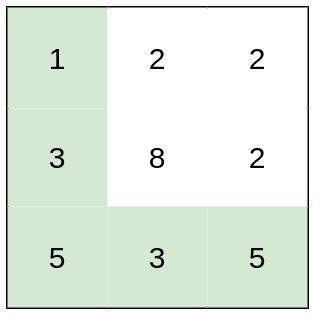
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

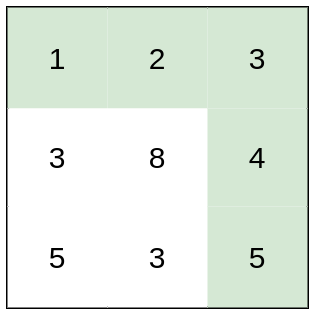
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

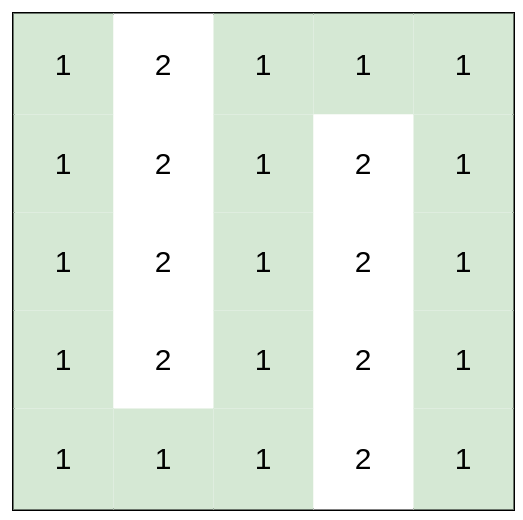
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 10^6

---

题意

在矩阵中找到一条从左上角到右下角的路径，使得该路径上所有相邻两个元素的差的绝对值的最大值最小。

思路

最短路问题，Dijkstra算法。

---

代码实现

Java

class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length, n = heights[0].length;
        int[][] e = new int[m][n];
        Queue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]);
        int[] xShift = {-1, 0, 1, 0}, yShift = {0, 1, 0, -1};
      
        for (int[] tmp : e) {
            Arrays.fill(tmp, Integer.MAX_VALUE);
        }
        e[0][0] = 0;
        q.offer(new int[]{0, 0, 0});

        while (!q.isEmpty()) {
            int[] cur = q.poll();
            if (cur[1] == m - 1 && cur[2] == n - 1) {
                return cur[0];
            }
            for (int i = 0; i < 4; i++) {
                int nX = cur[1] + xShift[i], nY = cur[2] + yShift[i];
                if (nX >= 0 && nX < m && nY >= 0 && nY < n) {
                    int nE = Math.max(cur[0], Math.abs(heights[nX][nY] - heights[cur[1]][cur[2]]));
                    if (nE < e[nX][nY]) {
                        e[nX][nY]  = nE;
                        q.offer(new int[]{nE, nX, nY});
                    }
                }
            }
        }

        return -1;
    }
}