Description
设 \(F_n\) 表示用 \(1\times 2\) 的骨牌填满 \(2\times n\) 的矩阵的方案数,\(G_n\) 表示用 \(1\times 2\) 的骨牌填满 \(3\times n\) 的矩阵的方案数。给出 \(l,r,k\),分别求出:
对 \(998244353\) 取模。\(1\leq T\leq 5\),\(1\leq l\leq r\leq 10^{18}\),\(k\leq 501\)。
Solution
m=2
考虑第 \(i\) 列是竖着放还是横着放,\(F_i=F_{i-1}+F_{i-2}\),\(F_0=1\)。发现 \(F_i=f_{i+1}\)(其中 \(f_i\) 为斐波那契数列,\(f_1=f_2=1\))。为了方便,一开始就令 \(l,r\) 加 \(1\),我们实际上要求 \(\sum_{n=l}^r\binom{f_n}{k}\)。
直接带 \(f\) 不太好做,考虑通项公式:
不妨设 \(A=\frac{1}{\sqrt 5}\),\(B=-\frac{1}{\sqrt 5}\),\(x=\frac{1+\sqrt 5}{2}\),\(y=\frac{1-\sqrt 5}{2}\),则 \(f_n=Ax^n+By^n\)。注意到 \(\sqrt 5\) 在组合数上指标上不太好维护。根据 \(\binom n m=\frac{n^{\underline m}}{m!}\),考虑下降幂转普通幂的公式 \(x^{\underline k}=\sum_{i=0}^k\begin{bmatrix}k\\i\end{bmatrix}(-1)^{k-i}x^i\):
最后面的 \(\sum_{n=l}^r(x^jy^{i-j})^n\) 是个等比数列求和。这样就能 \(\mathcal O(k^2\log n)\) 计算了。注意:
-
特判公比为 \(1\) 的情况。
-
\(\sqrt 5\) 在 \(\bmod 998244353\) 意义下不存在,类似表示虚数的方法,将每个数表示成 \(A+B\sqrt 5\),加减乘除照样定义。最后算出来的答案一定满足 \(B=0\),不必担心。
除法 \(\frac{a+b\sqrt 5}{c+d\sqrt 5}=\frac{(a+b\sqrt 5)(c-d\sqrt 5)}{(c+d\sqrt 5)(c-d\sqrt 5)}=\frac{ac-5bd}{c^2-5d^2}+\frac{bc-ad}{c^2-5d^2}\sqrt 5\)。
m=3
先考虑求出递推式。\(G_i=3G_{i-2}+2\sum_{k\geq 1}G_{i-2k-2}\)。
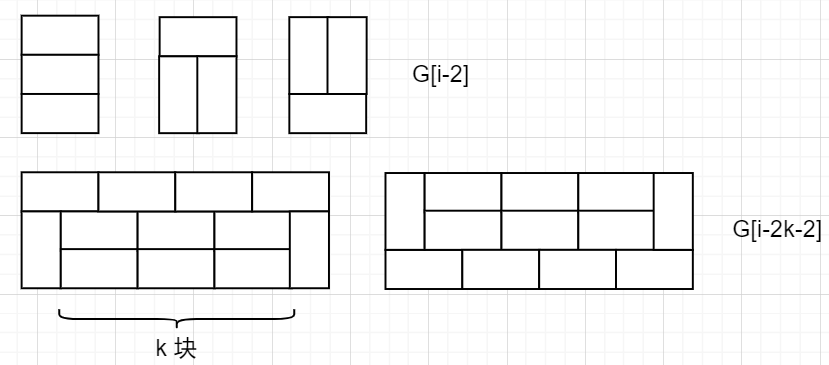
当 \(n\) 为奇数时答案为 \(0\),设 \(g_i=G_{2i}\),那么 \(g_i=3g_{i-1}+2\sum_{k=1}^{i-1}g_{i-k-1}=3g_{i-1}+2\sum_{k=0}^{i-2}g_k\)。
特征方程为 \(x^2=4x-1\),解得 \(x_1=2+\sqrt 3,x_2=2-\sqrt 3\)。则 \(g_i=Ax_1^n+Bx_2^n\)。再根据 \(g_0=1,g_1=3\):
然后就和 \(m=2\) 一样了。只是这里 \(l,r\) 没有 \(+1\) 而变成了 \(/2\)。
#include<bits/stdc++.h> #define ll long long using namespace std; const int N=510,mod=998244353; int t,m,w,c[N][N],s[N][N],inv[N],k,iv2=(mod+1)/2,tmp; ll l,r; int qpow(int x,int n){ int ans=1; for(;n;n>>=1,x=1ll*x*x%mod) if(n&1) ans=1ll*ans*x%mod; return ans; } struct num{ int x,y; num operator+(num a){return {(x+a.x)%mod,(y+a.y)%mod};} num operator-(num a){return {(x-a.x+mod)%mod,(y-a.y+mod)%mod};} num operator*(int a){return {1ll*x*a%mod,1ll*y*a%mod};} num operator*(num a){return {(1ll*x*a.x%mod+1ll*y*a.y%mod*w%mod)%mod,(1ll*x*a.y%mod+1ll*y*a.x%mod)%mod};} num operator/(num a){ int iv=qpow((1ll*a.x*a.x%mod-1ll*w*a.y%mod*a.y%mod+mod)%mod,mod-2); return {1ll*(1ll*x*a.x%mod-1ll*w*y%mod*a.y%mod+mod)%mod*iv%mod,1ll*(1ll*y*a.x%mod-1ll*x*a.y%mod+mod)%mod*iv%mod}; } }a,b,x,y; num qpow(num x,ll n){ num ans={1,0}; for(;n;n>>=1,x=x*x) if(n&1) ans=ans*x; return ans; } int calc(){ int ans=0; for(int i=0;i<=k;i++){ int cnt=0; for(int j=0;j<=i;j++){ num p=qpow(a,j)*qpow(b,i-j)*c[i][j],q=qpow(x,j)*qpow(y,i-j); q=q.x==1&&q.y==0?(num){(r-l+1)%mod,0}:(qpow(q,r+1)-qpow(q,l))/(q-(num){1,0}); cnt=(cnt+(p*q).x)%mod; } ans=(ans+1ll*((k-i)&1?mod-1:1)*s[k][i]%mod*cnt%mod)%mod; } return 1ll*inv[k]%mod*ans%mod; } signed main(){ inv[0]=inv[1]=1; for(int i=2;i<N;i++) inv[i]=1ll*inv[mod%i]*(mod-mod/i)%mod; c[0][0]=s[0][0]=1; for(int i=1;i<N;i++){ c[i][0]=1,inv[i]=1ll*inv[i-1]*inv[i]%mod; for(int j=1;j<=i;j++){ c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; s[i][j]=(1ll*s[i-1][j]*(i-1)%mod+s[i-1][j-1])%mod; } } scanf("%d%d",&t,&m); if(m==2) w=5,a=(num){0,1}/(num){5,0},b=(num){0,-1}/(num){5,0},x={iv2,iv2},y={iv2,mod-iv2}; else w=3,a=(num){3,1}/(num){6,0},b=(num){3,mod-1}/(num){6,0},x={2,1},y={2,mod-1}; while(t--){ scanf("%lld%lld%d",&l,&r,&k),tmp=qpow((r-l+1)%mod,mod-2); //注意后面 r-l+1 改变了 m==2?(l++,r++):(l=(l+1)/2,r/=2),printf("%lld\n",1ll*tmp*calc()%mod); } return 0; }