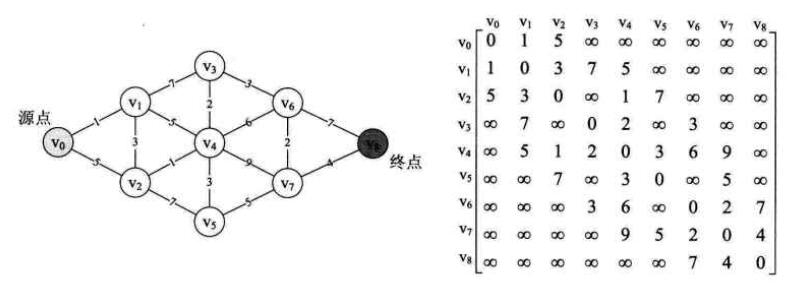
package dijkstra; import java.util.ArrayList; public class Dijkstra { private static int N = 1000; /*private static int[][] Graph = { { 0, 1, 5, N, N, N, N, N, N }, { 1, 0, 3, 7, 5, N, N, N, N }, { 5, 3, 0, N, 1, 7, N, N, N }, { N, 7, N, 0, 2, N, 3, N, N }, { N, 5, 1, 2, 0, 3, 6, 9, N }, { N, N, 7, N, 3, 0, N, 5, N }, { N, N, N, 3, 6, N, 0, 2, 7 }, { N, N, N, N, 9, 5, 2, 0, 4 }, { N, N, N, N, N, N, 7, 4, 0 } };*/ private static int[][] Graph = { { 0, 1, 1, N, N, 1, N, N, N }, { 1, 0, N, N, N, N, 1, N, N }, { 1, N, 0, 1, 1, N, N, N, N }, { N, N, 1, 0, N, N, N, N, N }, { N, N, 1, N, 0, N, N, 1, N }, { 1, N, N, N, N, 0, N, N, N }, { N, 1, N, N, N, N, 0, 1, N }, { N, N, N, N, 1, N, 1, 0, 1 }, { N, N, N, N, N, N, N, 1, 0 } }; public static void main(String[] args) { dijkstra(0, Graph,8); } /** * Dijkstra最短路径。 * 即图中"节点vs"到其它各个节点的最短路径。 * @param vs 起始节点 * @param Graph 图 * @param ds 目的终点 * 输入vs,Graph,ds输出选出的路径 * 每次选出一个最优节点加入最短路径数组中 */ public static void dijkstra(int vs, int[][] Graph,int ds) { int NUM = Graph[0].length; // 前驱节点数组 int[] prenode = new int[NUM]; // 最短距离数组 int[] mindist = new int[NUM]; // 该节点是否已经找到最短路径 boolean[] find = new boolean[NUM]; int vnear = 0; for (int i = 0; i < mindist.length; i++) { prenode[i] = i; mindist[i] = Graph[vs][i]; find[i] = false; } find[vs] = true; for (int v = 1; v < Graph.length; v++) { // 每次循环求得距离vs最近的节点vnear和最短距离min int min = N; for (int j = 0; j < Graph.length; j++) { if (!find[j] && mindist[j] < min) { min = mindist[j]; vnear = j; } } find[vnear] = true; // 根据vnear修正vs到其他所有节点的前驱节点及距离 for (int k = 0; k < Graph.length; k++) { if (!find[k] && (min + Graph[vnear][k]) < mindist[k]) { prenode[k] = vnear; mindist[k] = min + Graph[vnear][k]; } } } for (int i = 0; i < NUM; i++) { System.out.println("v" + vs + "...v" + prenode[i] + "->v" + i + ", s=" + mindist[i]); } int before=ds; int b=0; String q=null; ArrayList<String> array=new ArrayList<String>();//Java数组动态增加容量,采用ArrayList类数组,它可以在需要时自动扩容; array.add(String.valueOf(ds));//保存经过的路径节点 while(true) { b=prenode[before]; if(b==before) { break; } before=b; if(before==vs) { q=String.valueOf(before);//int型强转为String类型 array.add(q); break; } else { q=String.valueOf(before); array.add(q); } } array.add(String.valueOf(vs)); System.out.println(array);//输出找到的路径经过的点 } }