
解题思路:利用二叉搜索树性质

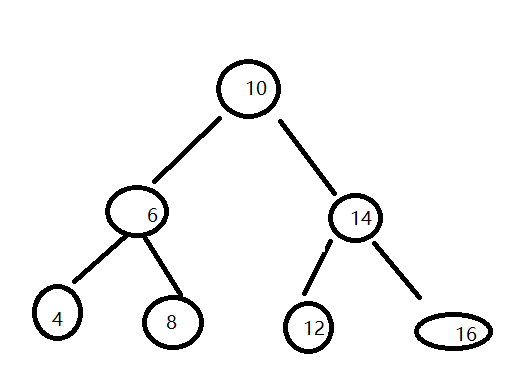
根据左子数节点<根节点,找出左子数集合和右子树集合。判断右子树集合满不满足>根节点。
可以确定10为根节点,
class Solution {
public:
vector<int> seq;
bool verifySequenceOfBST(vector<int> sequence) {
seq = sequence;
return dfs(0, seq.size() - 1);
}
bool dfs(int l, int r) {
if (l >= r) return true; //空树
int root = seq[r];
int k = l;
while(k < r && seq[k] < root) k ++; //找到根节点的左子树节点
for(int i = k; i < r; i ++) { //判断一下右子树里面的所有点都比根节点大,满足,则合法
if (seq[i] < root) //不满足,返回false
return false;
}
return dfs(l, k - 1) && dfs(k, r-1);//递归判断左右子树
//(左子树的右节点集合是不是 > 左子数根节点 && 右子树的右节点是不是 > 右子树根节点 )
}
};