动态规划的基本思想
动态规划的基本思想在于发现和定义问题中的子问题,这里子问题可也以叫做状态;以及一个子问题到下一个子问题之间 是如何转化的 也就是状态转移方程
因此我们遇到一个问题的时候 应该想一想这个问题是否能用某种方式表示成一个小问题,并且小问题具有最优子结构
最优子结构:问题的最优解由相关子问题的最优解组合而成,这些子问题可以独立求解
关于最优子结构 我们来看2个示例
1、求无权有向图中q-t的最短路径
如果q-t间的最短路径经过了点w 那么我们可以证明 q-w w-t也均是最短路径
所以无权有向图最短路径是具有最优子结构的
2、求无权有向图中q-t的最长的路径
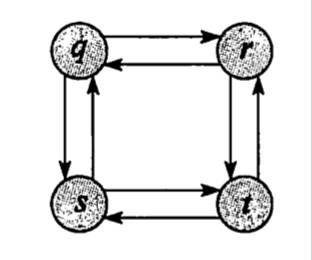
而无权有向图最长路径中
q-t的最长路径是是q-r-t 但 q-r缺不是q-r的最长路径 q-s-t-r是一条更长的路径
所以无权有向图最长路径不具有最优子结构
2、关于动态规划的另一个要点便是思考稍小的子问题和下一个子问题间是如何转化的也就是如何定义状态转移方程
状态转移方程的定义和我们是如何定义子问题的有关
比如:求最长连续回文串: 给出一个字符串S,求最长的连续回文串,例如串 babcbabcbaccba 最长回文是:abcbabcba
我们如果定义
p( i ) :以i结尾的最长回文串 我们会发现我们用子问题无法表示出p(i+1)
我们重新考虑一下原问题 最长连续回文串 如果用另一种方式来重新定义这个问题
已知字符串 S[0,n] 求回文传S[i,j]中最长的那一个
我们可以定义以下子问题
P(i,j) : S[i,j] 是否是一个回文, P(i,i) = true
那么我们可以定义如下的状态转换方程
P(i,j) ={ (P(i+1,j-1) && (Si == Sj) }
总结起来我们可以用以下步骤去考虑一个问题如何用动态规划来解决
1、思考问题的最后一个步骤 是如何通过选择构造得到最终答案的
2、根据构造情况来发现子问题
3、看看能否确定状态转移方程
动态规划与贪心等其他算法的比较
动态规划与分治,减治
分治 :将大问题分成若干个小问题去解决 递归的求解每个小问题,每个小问题之间没有关系 例如 快排
减治 :将大问题缩减成小问题,减掉的部分不需要考虑,例如:二分查找
动态规划:将原问题分成多个子问题,不同子问题间存在一定的联系,相互间有重叠的子问题
这里我个人认为动态规划分治 减治都是将大问题拆分成小问题 进行求解 区别在于
减治法减掉的部分 可以不用再求解了;
分治法每个小问题都需要进行求解;
动态规划不同的子问题间是有相互重叠的子问题的
动态规划与贪心
动态规划在于我们求解了所有子问题 虽然有些子问题最终并不能组成答案
而贪心算法任务无需求解所有子问题,所以选择在当前情况下最优的情况自顶向下的求解问题,贪心可以认为是动态规划的一个特例
如果用一个树来表示子问题的话 可以认为动态规划考虑了树中的所有节点
而贪心算法减去了树了许多枝干,在考虑了通向最优解的那一条路
常见的可以用动态规划解决的问题
1、最大连续子序列和:
给定k个整数的序列{N1,N2,...,Nk },其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj },其中 1 <= i <= j <= k。最大连续子序列是所有连续子序中元素和最大的一个,
例如给定序列{ -2, 11, -4, 13, -5, -2 },其最大连续子序列为{11,-4,13},最大连续子序列和即为20。
2、最大连续子序列乘积:
给一个浮点数序列,取最大乘积连续子串的值,例如 -2.5,4,0,3,0.5,8,-1,则取出的最大乘积连续子串为3,0.5,8。也就是说,上述数组中,3 0.5 8这3个数的乘积30.58=12是最大的,而且是连续的。
3、求最长连续回文串:
给出一个字符串S,求最长的连续回文串,例如串 babcbabcbaccba 最长回文是:abcbabcba
4、字符串相似度:
把两个字符串变成相同的基本操作定义如下:
1. 修改一个字符(如把 a 变成 b)
2. 增加一个字符 (如 abed 变成 abedd)
3. 删除一个字符(如 jackbllog 变成 jackblog)
针对于 jackbllog到jackblog 只需要删除一个或增加一个 l 就可以把两个字符串变为相同。把这种操作需要的次数定义为两个字符串的距离 L, 则相似度定义为1/(L+1) 即距离加一的倒数。那么jackbllog和jackblog的相似度为 1/1+1=1/2=0.5 也就是所两个字符串的相似度是 0.5。
给定任意两个字符串,你是否写出一个是否来计算出它们的相识度。
5、最长公共子序列
对于序列S和T,求它们的最长公共子序列。例如X={A,B,C,B,D,A,B},Y={B,D,C,A,B,A}则它们的lcs是{B,C,B,A}和{B,D,A,B}。求出一个即可。
针对最大连续子序列乘积给出一段讲解与代码
最大连续子序列和:
给定k个整数的序列{N1,N2,...,Nk },其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj },其中 1 <= i <= j <= k。最大连续子序列是所有连续子序中元素和最大的一个,
例如给定序列【-2, 11, -4, 13, -5, -2】,其最大连续子序列为{11,-4,13},最大连续子序列和即为20。
思路:
20这个答案 是我们比较了【-2】,【11】,【-4】,【-2,11,-4,11】,【11,-4,13】,【11,-4,13,-5】,【11,-4,13,-5。-2】这几个序列之后得到
所以我们定义子问题是
Max(i) : 以i结尾的连续序列的最大和
状态转移方程是:
Max[i] = max{a[i], Max[i-1] + a[i])
代码如下:
int maxSubArray(int A[], int n) {
int ans=A[0],i,j,sum=0;
for(i=0;i<n;i++){
sum+=A[i];
ans=max(sum,ans);
sum=max(sum,0);
}
return ans;
}