插入排序
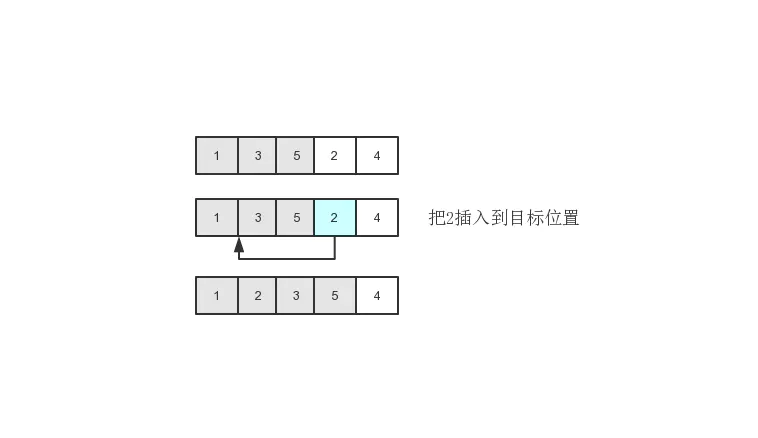
上图演示了第4次遍历,此时元素1、3、5已经是有序序列,待排的元素是2,要把它插入到1和3之间。此时3和5都往后移动了一位。
可以看出该算法的核心是:如何在有序序列里找到正确的插入位置?
思路是从有序序列的尾部开始,逐个与目标元素比较,如果大于目标元素,该元素需要后移。
代码实现:
for (let j = 1; j < array.length; j++) { let i = j let target = array[i] while(i > 0 && array[i-1] > target) { array[i] = array[i-1] i-- } array[i] = target }
插入排序不需要额外空间,是本地排序,相等元素是不会交换前后顺序,因而也是稳定排序,时间复杂度为O(n^2),适用于少量数据排序。
相比冒泡排序和选择排序,插入排序的使用相对多一些。因为前两者是交换排序,本质上需要3次原子操作的。
快速排序
快速排序的特点就是快,而且效率高!它是处理大数据最快的排序算法之一。
思想
- 先找到一个基准点(一般指数组的中部),然后数组被该基准点分为两部分,依次与该基准点数据比较,如果比它小,放左边;反之,放右边。
- 左右分别用一个空数组去存储比较后的数据。
- 最后递归执行上述操作,直到数组长度 <= 1;
特点:快速,常用。
缺点:需要另外声明两个数组,浪费了内存空间资源。
const quickSort1 = arr => { if (arr.length <= 1) { return arr; } //取基准点 const midIndex = Math.floor(arr.length / 2); //取基准点的值,splice(index,1) 则返回的是含有被删除的元素的数组。 const valArr = arr.splice(midIndex, 1); const midIndexVal = valArr[0]; const left = []; //存放比基准点小的数组 const right = []; //存放比基准点大的数组 //遍历数组,进行判断分配 for (let i = 0; i < arr.length; i++) { if (arr[i] < midIndexVal) { left.push(arr[i]); //比基准点小的放在左边数组 } else { right.push(arr[i]); //比基准点大的放在右边数组 } } //递归执行以上操作,对左右两个数组进行操作,直到数组长度为 <= 1 return quickSort1(left).concat(midIndexVal, quickSort1(right)); }; const array2 = [5, 4, 3, 2, 1]; console.log('quickSort1 ', quickSort1(array2)); // quickSort1: [1, 2, 3, 4, 5]