斐波那契搜索技术是一种使用分而治之算法搜索已排序数组的方法,该算法借助斐波纳契数来缩小可能的位置。与二元搜索相比,排序数组被分成两个大小相等的部分,其中一个进一步检查,斐波那契搜索将数组分成两个部分,其大小为连续的斐波纳契数。平均而言,这导致执行的比较增加了大约4%,但它的优点是只需要加法和减法来计算被访问数组元素的索引,而经典二进制搜索需要比特移位,除法或乘法,这些操作在Fibonacci搜索时首先不常见出版。Fibonacci搜索具有O(log n)的平均和最差情况复杂度。
总的来说是二分查找的一个优化。
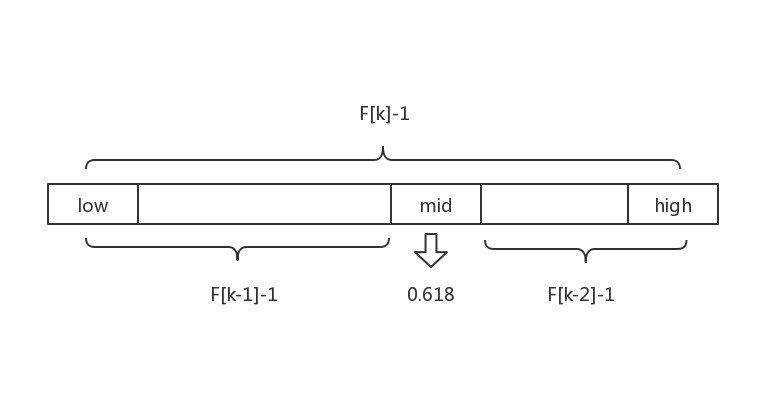
Fibonacci序列具有一个数字是其前面两个连续数的总和的属性。因此,可以通过重复添加来计算序列。两个连续数字的比率接近黄金比率,1.618 ...二进制搜索通过将搜索区域除以相等的部分(1:1)来工作。Fibonacci搜索可以将其分成接近1:1.618的部分,同时使用更简单的操作。
构建斐波那契序列数组(越到后面,前一个数与后一个数的比例接近0.618):
1 //构建斐波那契数列 2 public static void fibonacci(int[] F) { 3 F[0] = 0; 4 F[1] = 1; 5 for (int i = 2; i < max_size; ++i) 6 F[i] = F[i - 1] + F[i - 2]; 7 System.out.println(Arrays.toString(F)); 8 }
斐波那契查找算法:
1 public static int fibonacciSearch(int[] a, int n, int key) { 2 int low = 0; 3 int high = n - 1; 4 5 int F[] = new int[max_size]; 6 fibonacci(F);//构建斐波那契数组 7 8 //计算 n 位于斐波那契数列的位置 9 int k = 0; 10 while (n > F[k] - 1) 11 ++k; 12 13 //将数组a扩展到F[k]-1的长度 14 int tmp[]; 15 tmp = new int[F[k] - 1]; 16 System.arraycopy(a, 0, tmp, 0, n); 17 18 for (int i = n; i < F[k] - 1; ++i) 19 tmp[i] = a[n - 1];//用数组最后一个元素扩展 20 21 while (low <= high) { 22 int mid = low + F[k - 1] - 1;//借助斐波纳契数确定位置 23 if (key < tmp[mid]) { 24 high = mid - 1; 25 k -= 1; 26 } else if (tmp[mid] < key) { 27 low = mid + 1; 28 k -= 2; 29 } else { 30 if (mid < n) 31 return mid; 32 else 33 return n - 1; 34 } 35 } 36 tmp = null; 37 return -1; 38 }
如果被搜索的元素具有非均匀访问存储器存储(即,访问存储位置所需的时间根据所访问的位置而变化),则斐波那契搜索可能具有优于二分搜索的优势,从而略微减少访问所需的平均时间存储位置。
最坏情况下,时间复杂度为O(log2n),且其期望复杂度也为O(log2n)。
测试代码:
1 public static void main(String[] args) { 2 int a[] = {0, 16, 24, 35, 47, 59, 62, 73, 132}; 3 int key = 132; 4 int index = fibonacciSearch(a, a.length, key); 5 System.out.println(key + " is located at " + (index+1)); 6 }