选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小元素(这里只考虑升序),存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小元素,然后准确放到已排序序列中(数组前面)。因此,这个算法主要维护数组中两个子数组,一个是已排序的子数组,另一个是剩下未排序的数组。
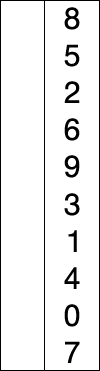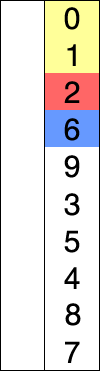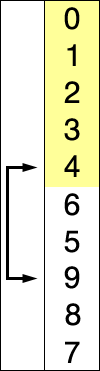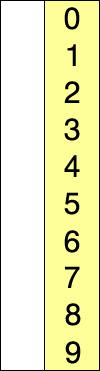
在选择排序的每次迭代中,都会从未排序的子数组中选取最小元素(这里只考虑升序)并将其移至已排序的子数组中。
选择排序的主要优点与数据移动有关。如果某个元素位于正确的最终位置上,则它不会被移动。选择排序每次交换一对元素,它们当中至少有一个将被移到其最终位置上,因此对 n 个元素的表进行排序总共进行至多(n - 1)次交换,交换永远不会超过 O(n)。在所有的完全依靠交换去移动元素的排序方法中,选择排序属于非常好的一种,特别是在内存中写入是一项非常昂贵的操作时非常有用。
/** * 选择排序算法的实现 * * @param arrays 需要排序的数组 * @param n 数组长度 */ private static void selectionSort(int[] arrays, int n) { int i, j, minIndex; for (i = 0; i < n; i++) { minIndex = i; // 记录最小数值的索引 for (j = i + 1; j < n; j++) { if (arrays[j] < arrays[minIndex]) { minIndex = j; } } if (minIndex > i) swap(arrays, i, minIndex); } }
代码用了两个嵌套 for 循环,其时间复杂度都是 O(n²),辅助空间为 O(1),是一种 in-place 排序,不需要额外的空间。
选择排序为不稳定排序,比如说 5, 8, 5, 2, 1,第一个 5 与第四个 2 交换,原始的两个 5 的顺序发生变化,因而为不稳定排序。
-
平均时间复杂度: O(n^2)
-
空间复杂度: O(1)
-
稳定性: 不稳定(不过可以实现稳定)
测试代码
1 public static void main(String[] args) { 2 int[] arr = {1, 1, 2, 0, 9, 3, 12, 7, 8, 3, 4, 65, 22}; 3 4 SelectionSort.selectionSorts(arr, arr.length); 5 6 for(int a : arr){ 7 System.out.print(a + " "); 8 } 9 }