由于经常需要进行摄像机标定,所以对张正友标定算法做了一个总结。其实可以参考以下博客:
http://blog.csdn.net/u010128736/article/details/52860364
http://blog.csdn.net/pinbodexiaozhu/article/details/43373247
一、相机模型
要理解摄像机标定,首先要理解基于小孔成像的相机成像模型,下面分析小孔成像模型并给出整个投影过程。
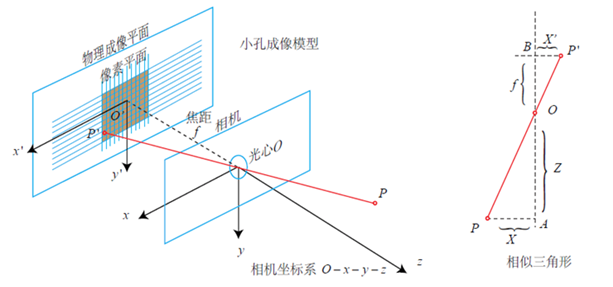
如图所示,(X,Y,Z)表示物体在相机坐标系(以光心为坐标原点,光轴为Z轴,如上图所示),(X',Y')表示物体在成像平面上的坐标,则根据三角形相似 可以得出:

去负号可得(表示物理成像面在光心之前,不影响计算):
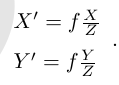
上面的过程表示将一个相机坐标系下的一点投影到了相机成像面上,下面则要将物理成像面(物理成像坐标系)上的点转换到像素面(像素坐标系)上,像素坐标系原点一般定义在左上角,故物理成像面到像素成像面可以描述成一个缩放加一个平移:

其中: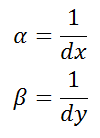 ,dx,dy为传感器单个像素在不同方向上的长度,cx,cy图像像素的中心值。
,dx,dy为传感器单个像素在不同方向上的长度,cx,cy图像像素的中心值。
故,结合前面小孔成像可得:

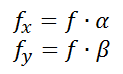
![]() 的物理意义为焦距长度上像素个数。
的物理意义为焦距长度上像素个数。
将上面的结论写成矩阵形式即为:

这里的K矩阵就是我们需要标定的相机内参数。
通常情况下,我们不知道一个点在相机坐标系下的坐标,但却可以任意定义一个世界坐标,每一个点都有其绝对的世界坐标值,如果要得到相机坐标系的坐标值,需要求解相机的位姿矩阵,即外参:

这里的Pw为世界坐标系下一点,R,t为旋转和平移矩阵,T表示位姿矩阵(含旋转和平移),也称为外参矩阵。
总结前面的投影过程为:
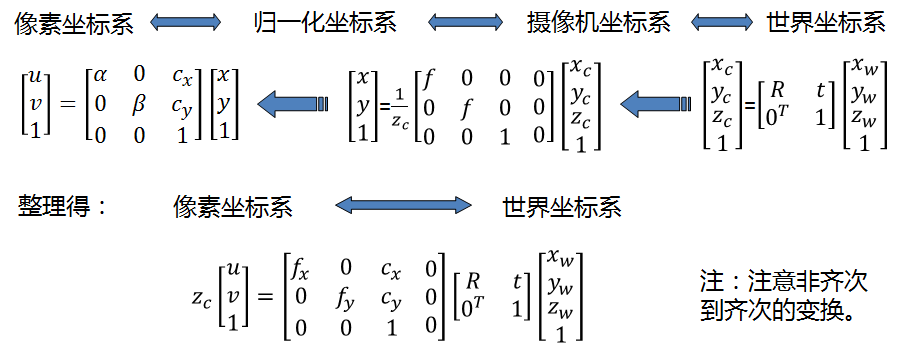
相机标定还必须考虑的一点是畸变参数,畸变可以分为径向畸变、切向畸变、薄棱镜畸变等,下图描述了切线方向和半径方向的畸变示意图:

径向畸变又可分为两种,桶形和枕形失真,它是由镜头引入的:

切向畸变主要是传感器和镜头的不平行引入的:
这里只给出径向和切向畸变的数学模型,具体可以参考:
径向畸变多项式:

其中,
![]()
切向畸变多项式:

一般畸变系数包含上述k1,k2,p1,p2,k3。
二、张正友标定算法

基本方程:
根据前面的投影过程,下述投影过程容易理解,其中s为任意比例系数:

在张氏标定法中,通常假设模型平面在世界坐标系的Z=0的平面上,所以上式可以整理为:

简写为:

其中H称为单应矩阵,反映的是Z=0平面到像素平面的变换关系:

张氏标定法中棋盘格之间的距离是已知的,以9*6的棋盘格为例,每个方格的距离应是30mm,也就是每个角点的世界坐标是已知的,像素坐标通过角点检测获得,故单应矩阵现在是可以求取的(至于如何求取单应矩阵,还请自行了解),最少使用4个点可以求得单应矩阵。
下面则是求解各个矩阵,首先令H为:
![]()
则容易得出以下结论:
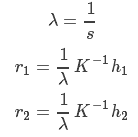
由于旋转矩阵的单位正交性,所以有以下约束存在:
![]()
故可以得到两个关于内参的基本方程:
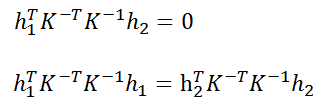
因此,按照前面的分析,一个单应矩阵可以获得两个K的约束,故最少需要2幅图像才能求得四个内参,如果是5个内参,至少需要3幅图像。(单应矩阵的求取方法要求每幅图像有至少4个对应点。)
具体的求解方法由于不涉及标定理论,就不再展示,但可以参考计算机视觉或机器视觉书,上面有详细的计算过程。
三、小结
标定结果应该至少包含以下内容:

张氏标定法应用广泛,在OpenCV中给出张氏标定的函数接口,所以应用也是非常方便,对于大部分的相机标定任务张氏标定法都能胜任。