本讲内容
1. Kernels （核）
2. L1 norm soft margin SVM （L1 norm软边界SVM）
3. SMO algorithm （SMO算法）
1. 核函数K
首先回顾线性分类器SVM的原始优化问题
上一讲解出其对偶问题为
解出
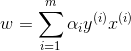
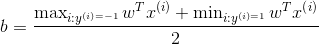
我们可以将整个算法表示成内积的形式
由上式可知，算法对于x的依赖，仅仅局限于这些内积，我们甚至无需显式地写出x的值，只需要得到训练样本
和输入特征向量x之间内积的值。
这就是核要解决的事情。
给定一组输入特征x，我们经常会将这个特征x映射到一组更高维的特征上，用 
来表示这个映射关系，那么有
Have 
，
得到新特征
.
如果想要使用这些新特征 ，只需要回到原来的公式中，将所有的 
替换为 
这里存在一个问题，映射之后得到的新特征 的维数可能非常高，甚至于是无限维的向量，那么传统的计算向量内积的方法是非常低效的，因为计算机需要对进行表示，之后才计算内积。
既然 的表示代价如此之大，那么干脆就不要显式的把表示出来——我们可以通过直接规划的值来得到我们需要的结果。
引入核函数的定义
SVM的思想是，对于算法中任何出现 的地方，都替换为核函数 
。
假设对于 
我们规划 
下面比较传统计算内积的算法和核函数计算内积算法的复杂度：
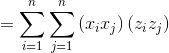
那么对应的
（假设n=3）
对于传统算法来说，假设x的长度n为3，那么为了显式的表示出 ，需要O(n^2)的时间复杂度，如图所示 的长度为9；
但是如果只是计算核函数K的值，只需要O(n)的时间复杂度：我们计算 
的值，然后将结果乘积。
通过创造核函数的形式，实际上在隐性地处理一个维数非常大的向量空间的乘积，而仅仅需要O(n)的时间复杂度。
那么对于一个机器学习问题，应该如何创造一个核？
给定一组属性 
给定一组属性 
核就是计算 
一种直观的理解是：
假设属性x和属性z相似度很高，那么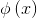 
和 
将会大概指向相同的方向，内积会比较大；
如果x和z的相似度很低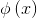， 将会指向不同的方向，内积会比较小。
因此一个创造核的一般做法是：
当你希望x和z相似度高的时候，K(x,z)的值比较大；
当你希望x和z相似度低的时候，K(x,z)的值比较小。
一种好的度量x和z相似性的核函数为
核K的合法性：
是否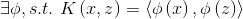 
？
假设K是一个核函数， 给定任意点集合 
定义核矩阵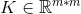 
对于任何一个m维向量 
因此，当核矩阵K为对称的半正定矩阵时，K是一个合法的Mercer核，即 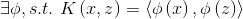，逆命题也成立。
2. L1 norm soft margin SVM
到目前为止，我们讨论SVM时认为数据是线性可分的, 把数据映射到高维空间一般会增加线性可分的可能性，但是我们不能保证一定可以.
左图显示的是一个最优间隔分类器，但是如果在左上区域加上一个异常值，决定边界线会发生剧烈的变化，
导致分类器有更小的边界.
为了使算法能够处理非线性可分的数据集并且对异常值不会这么敏感, 修订优化问题如下：
直观解释如下：
意味着样本被正确分类，通过设置 
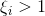，我们允许分类器对一部分样本错误分类；
然而这种做法并不被鼓励，因此需要在原始的优化问题上添加一个正则项，当将 
设置为较大值时，会给予总体目标一些惩罚。
这里多了一个参数，于是对偶问题的解变为
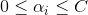
通过KKT条件，可以推导出如下收敛性条件：
3. 顺序最小优化算法
我们得到了优化问题以及收敛性条件，那么该如何高效地求解这个优化问题呢？
引子. 坐标上升法
对于上述优化问题，首先忘掉所有约束条件，只考虑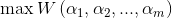 
坐标上升算法表述为
Repeat
{
for i = 1 to m:
}
保持除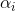 
之外的所有参数固定，使优化目标相对于
取最大值。
坐标上升法对于二次函数的执行过程如下：
坐标上升法相对于牛顿法，会需要更多的迭代次数来达到收敛，但是优点是，当每次固定所有参数只优化一个参数时，其计算代价要比牛顿法的一次迭代小得多。
下面考虑坐标上升法在SVM求解优化问题的引申，考虑SVM的约束：
如果使用坐标上升法，不可能一次只改变一个 
而不违反约束条件。
于是SMO算法选择一次更新两个
。
假设更新的参数为 
，对于算法的每一次迭代，都有
因此
将
用 
表示
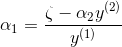
于是在一次迭代中，可以把 
看成是 的函数
是标准的一元二次函数，可以很容易的得到关于 的最优解。
然后考虑另外一个约束
称为方形约束。
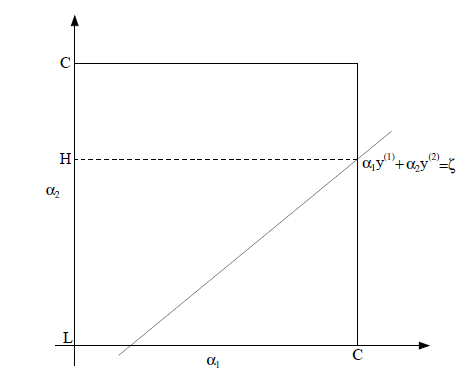
的解一定要落在边长为C的正方形的空间内，同时 还要满足 的约束，即 要落在这条直线上，那么根据求解的一元二次函数的最优解， 的更新如下：
求出之后根据
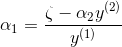
解出 的值，一次迭代完成。
每次迭代需要根据一些启发性规则选出 
来进行更新，直到收敛。
第八讲完。