本讲内容:
1.locally weighted regression (局部加权回归算法)
2.Probabilistic interpretation of linear regression (线性回归的概率解释)
3.Logistic regression (逻辑回归算法)
4.Digression Perceptron (感知器算法)
欠拟合与过拟合
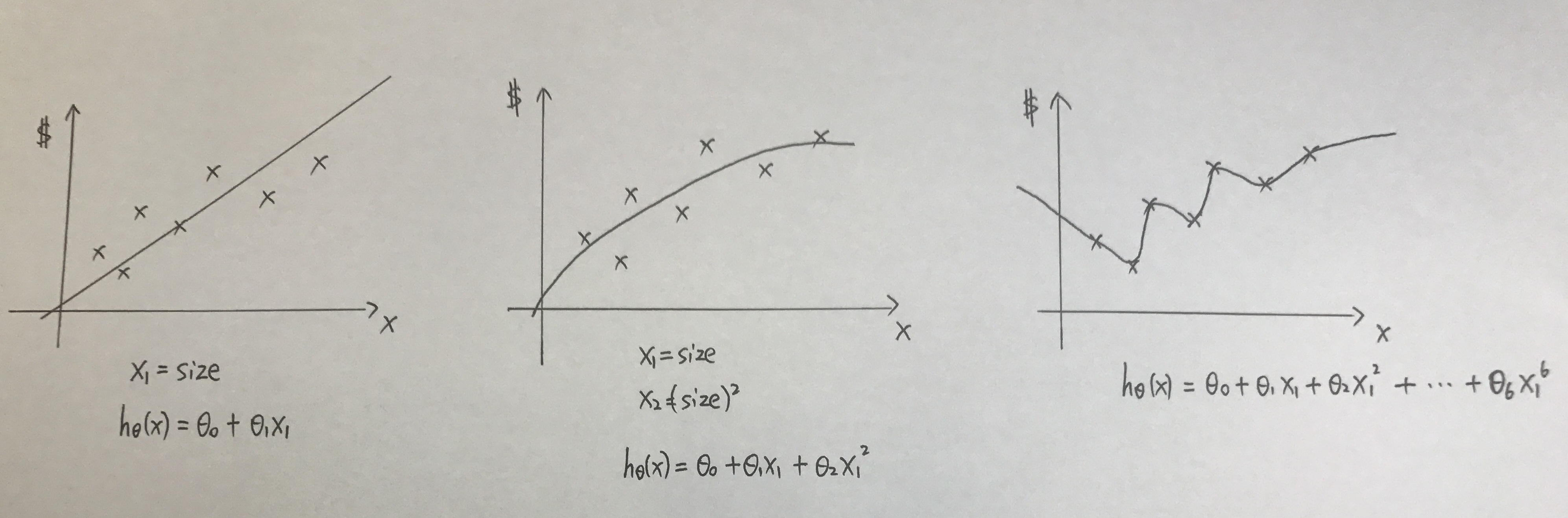
对于只包含这7个点的数据集来说,左2图(二次模型)最好的拟合了数据的特性。左1(线性模型)忽视了数据中的某些二次成分,而右1(6次模型)又过分地拟合了这七个点。
过大(右1)的特征集合,会使得到的模型过于复杂,这种情况称之为overfitting(过拟合);
过小(左1)的特征集合,会使得到的模型过于简单,这种情况称之为underfitting(欠拟合);
因此,特征的选择,对于算法的性能,是至关重要的。
那么问题是,怎样选取合适的特征,可以得到拟合特性最好的模型?
(1)在之后某一讲中,会提到特征选择算法,这是一类自动化的算法,可以在这类回归问题中选择要用到的特征。
(2)non-parametric learning algorithms 非参数化学习算法,可以在一定程度上缓解对于选取特征的需求。
定义:parametric learning algorithms 参数化学习算法, 是一类有固定数目的参数,以用来进行数据拟合的算法。
线性回归属于参数化学习算法。线性回归中,有一个固定的 集合,一定可以拟合数据。
集合,一定可以拟合数据。
non-parametric learning algorithms 非参数化学习算法
定义:non-parametric learning algorithms 非参数化学习算法,是一类参数数量会随着m增长的算法,m代表训练集合的大小。
局部加权回归属于非参数化学习算法。
1.局部加权回归 /Loess

对于确定的查询点x,在x处对假设h进行求值:
对于线性回归:
(1) fit  to minimize
to minimize 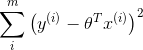
(2) return 
对于局部加权回归,工作有点不同:
对于查询点x,检查数据集合,然后只考虑位于x周围固定区域内的数据点,之后对这个数据子集使用线性回归来拟合出一条直线。
(1) fit  to minimize
to minimize 
where 
if  small, then
small, then 
if  large, then
large, then 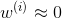
 称为权值,对于和x离得近的点,赋予较大的权值;和x离得远的点,赋予较小的权值。
称为权值,对于和x离得近的点,赋予较大的权值;和x离得远的点,赋予较小的权值。
(2) return 
更一般地,
 称作波长函数,控制权值随距离下降的速率。
称作波长函数,控制权值随距离下降的速率。
2.线性模型的概率解释
提出问题:在回归问题中,为什么选择最小二乘估计作为我们的优化目标?
首先假设输出和输入有如下的映射关系:

在房屋问题中,除了面积或者卧室数量之外,可能还存在一些我们没有捕获的特征,他们也对房屋的价格存在影响,这种影响可以看做随机噪声。
 意味着误差项,即我们未捕获特征以及其他随机噪声对房屋价格的影响总和。
意味着误差项,即我们未捕获特征以及其他随机噪声对房屋价格的影响总和。
假设 服从高斯分布,即
服从高斯分布,即 

这表示,在给定参数的时候,房屋的价格也服从高斯分布:


假设 独立同分布
独立同分布
公式
 称为参数
称为参数 的似然性
的似然性


极大似然估计(Maximum likelihood):选择 使得数据出现的可能性尽可能大
使得数据出现的可能性尽可能大
定义 对数似然函数
对数似然函数


因此 等价于
等价于
等价于最小化  注意到最终结果与
注意到最终结果与 无关
无关
该函数即为我们上一讲选择的成本函数
3.逻辑回归
分类:回归问题预测的变量y是连续变量,而分类问题中预测的变量y是离散变量。这里讨论二元分类,即限定
对分类问题使用线性回归可能是一个糟糕的主意。线性回归的预测值可能大于1,也可能小于0,而我们希望我们的假设预测的输出值在0,1 之间。
所以我们不选择线性函数作为假设,而选择

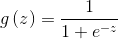 称为sigmoid function 或者 logistic function.
称为sigmoid function 或者 logistic function.
 的图像如下
的图像如下

概率意义上的解释:
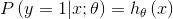

将上述二式写在一起:

做参数的极大似然估计
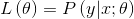




为了使对数似然函数最大化,采样梯度上升法更新 的值,之所以是上升而不是下降,是因为这里需要的是
的值,之所以是上升而不是下降,是因为这里需要的是 的极大值
的极大值






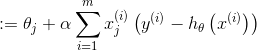
4.感知器算法

代替 logstic function: 

该函数生成的值只有0,1,所以为该函数赋予概率意义十分困难。
使用梯度上升法更新参数
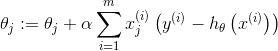
第三讲完。