问题描述
Excel单元格的地址表示很有趣,它使用字母来表示列号。
比如,
A表示第1列,
B表示第2列,
Z表示第26列,
AA表示第27列,
AB表示第28列,
BA表示第53列,
....
当然Excel的最大列号是有限度的,所以转换起来不难。
如果我们想把这种表示法一般化,可以把很大的数字转换为很长的字母序列呢?
本题目即是要求对输入的数字, 输出其对应的Excel地址表示方式。
比如,
A表示第1列,
B表示第2列,
Z表示第26列,
AA表示第27列,
AB表示第28列,
BA表示第53列,
....
当然Excel的最大列号是有限度的,所以转换起来不难。
如果我们想把这种表示法一般化,可以把很大的数字转换为很长的字母序列呢?
本题目即是要求对输入的数字, 输出其对应的Excel地址表示方式。
样例输入
26
样例输出
Z
样例输入
2054
样例输出
BZZ
数据规模和约定
我们约定,输入的整数范围[1,2147483647]
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
思路
看到题目的第一思路:进制转换问题~~~
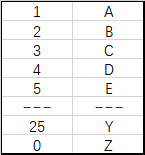
但是按照进制转换思路写了之后,通过率没有100%。不过思路并没有出错,但是与一般的进制转换问题不同的是,我们的进制转换没有 0 位,所以在对A和Z的处理上稍微注意一下,因为如果我们输入的数是26的倍数的话,因为没有0位,比如26的表示为Z,但52的表示为AZ,但是如果我们对52不停短除26,会发现结果为[2, 0]。与下图的字典对照会发现应该为BZ,很明显多了一个26。计算机对数的取模运算是会取到0的,我们的开始的26个字母也是有用0来表示的,因此26我们可以想象成[ ]Z(空格Z)。
所以进制转换的思想就是:逢Z减Z。即如果这个数可以被26整除,那么我们减去一个26。
比如对于AZCZ:
表示为1*26^3 + 26*26^2 + 3*26^1 + 26*26^0
短除过程为:
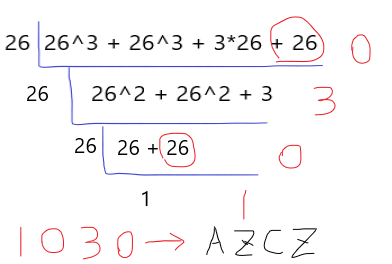
算法如下

1 #include<iostream> 2 #include<map> 3 #include<vector> 4 5 using namespace std; 6 7 typedef map<int, char> mp; 8 typedef map<int, char>::value_type init; 9 10 mp INITmp() 11 { // 为了看起来更符合我们的直观感受,这里还是用了字典 12 mp ch; 13 ch.insert(init(0, 'Z')); 14 for(int i=0;i<25;i++){ 15 ch.insert(init(i+1, i + 'A')); 16 } 17 return ch; 18 } 19 20 int main() 21 { 22 int x=0; 23 mp dic = INITmp(); 24 while(cin>>x) 25 { 26 vector<char> s; 27 while(x) 28 { 29 s.push_back(dic[x%26]); 30 // 这里是核心代码,逢Z减Z,其余的地方与进制转换问题无二! 31 if(x%26 == 0) x -= 26; 32 x /= 26; 33 } 34 // 依然是倒序输出 35 for(int i=s.size()-1;i>=0;i--){ 36 cout<<s.at(i); 37 } 38 cout<<endl; 39 } 40 41 return 0; 42 }
