1.正规式转换到正规文法
对任意正规式R选择一个非终结符Z生成规则Z→R
1.对形如A→ab的规则,转换成A→aB,B→b
2.将形如A→a|b的规则,转换成A→a,A→b(A→a|b)
3.将形如A→a*b的规则,转换成A→aA,A→b
将形如A→ba*的规则,转换成A→Aa,A→b
不断利用上述规则进行转换,直到每条规则最多含有一个终结符为止.
1(0|1)*101
(a|b)*(aa|bb)(a|b)*
((0|1)*|(11))*
(0|110)
答:
1(1)S -> A1
A -> B0
B -> C1
C -> 1(0|1)* -> C(0|1)|1 -> C0|C1|1
1(2)S -> S(a|b)
S -> (a|b)*(aa|bb) -> (a|b)S|aa|bb
所以:S -> Sa|Sb|aS|bS|aA|bB
A -> a
B -> b
1(3)S -> ε|((0|1)*|(11))S -> ε|(0|1)*S|11S
S -> (0|1)*S -> (0|1)S|S
S -> 11S -> 1A
A -> 1S
所以:S -> ε|0S|1S|1A
A -> 1S
1(4)S -> ε|(0|11*0)S -> ε|0S|11*0S
S -> 11*0S -> 1A
A -> 1*0S -> 1A
A -> 0S
所以:S -> ε|0S|1A
A -> 1A|0S
2. 自动机M=({q0,q1,q2,q3},{0,1},f,q0,{q3})
其中f:
(q0,0)=q1
(q1,0)=q2
(q2,0)=q3
(q0,1)=q0
(q1,1)=q0
(q2,1)=q0
(q3,0)=q3
(q3,1)=q3
画现状态转换矩阵和状态转换图,识别的是什么语言。
答:现状态转换矩阵
| q0 | q1 | q2 | q3 | |
| 0 | q1 | q2 | q3 | q3 |
| 1 | q0 | q0 | q0 | q3 |
状态转换图:
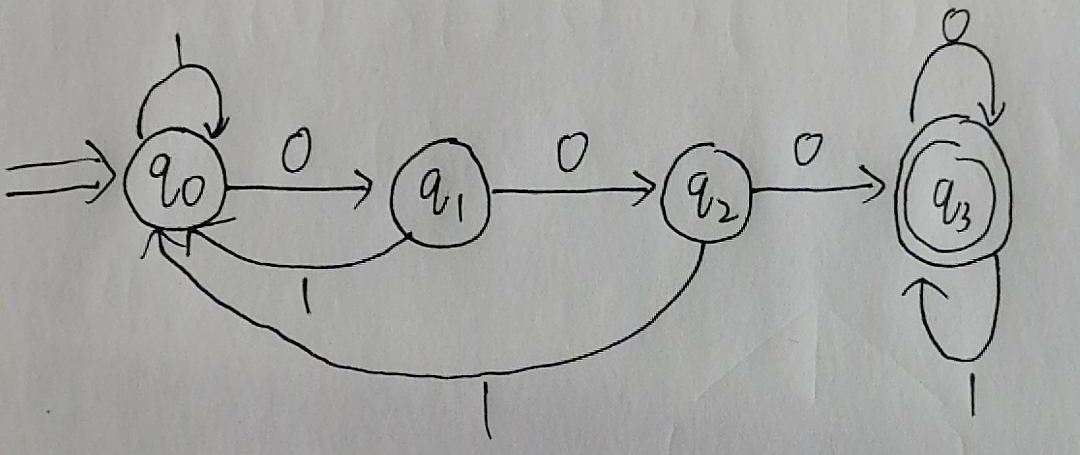
语言:(1*(01)*01)*0(0|1)*
3.由正规式R 构造 自动机NFA
(a|b)*abb
(a|b)*(aa|bb)(a|b)*
1(1010*|1(010)*1)*0
答:
