递归练习（课程作业）

一、使用计算机计算组合数：

1.程序设计思想：

a)使用组合数公式利用阶乘计算：

　　定义一个求阶乘的方法fac(int n)，fac为递归定义，当 n 不小于1时，返回n*(n - 1)!即n * fac(n - 1)，否则返回1。程序接收数据n，k后直接利用组合数公式调用fac方法进行计算：输出fac(n) / (fac(k) * fac(n - k))。

b)使用递归的方法用组合数递推公式计算：

　　定义求组合数函数C(n,k)当k = 0或n = k时，返回1，否则，根据递推公式，C(n,k) = C(n - 1,k - 1) + C(n - 1,k)。

c)使用杨辉三角形求组合数：

　　定义一个二维数组Y存储杨辉三角形，循环赋值构造杨辉三角形：Y[i][0] = 1,Y[i][i] = 1,(i = 0,1,2……n)，其余每个Y[i][j] = Y[i - 1][j - 1] + Y[i - 1][j]。则C(n,k)就等于Y[n][k]。

2.程序流程图：

 

　　　　　　

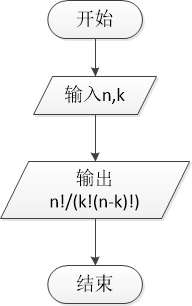
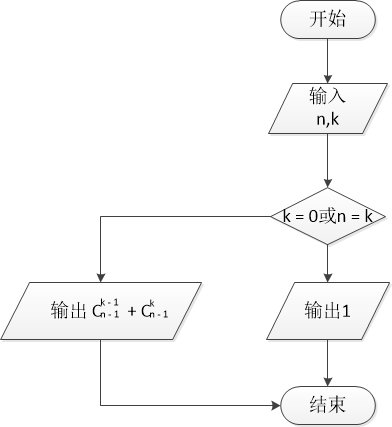
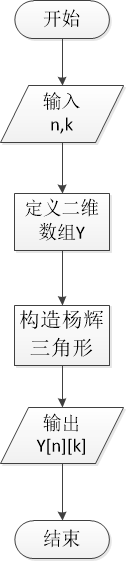
3.程序源代码：

//使用组合数公式利用n!计算C(n,k)
import java.util.*;
public class Combination {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n,k;
        n = in.nextInt();
        k = in.nextInt();
        
        System.out.println(C(n,k));
    }
    public static int fac(int n){
        if(n <= 1)
            return 1;
        return n * fac(n - 1);
    }
    public static int C(int n,int k){
        return fac(n) / (fac(k) * fac(n - k));
    }
}

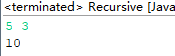
//使用递归的方法用组合数递推公式计算
public class Recursive {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n,k;
        n = in.nextInt();
        k = in.nextInt();
        
        System.out.println(C(n,k));
        in.close();
    }
    public static int C(int n,int k){
        if(k == 0 || n == k)
            return 1;
        return C(n - 1,k - 1) + C(n - 1,k);
    }
}

//使用递推的方法用杨辉三角形计算
public class Yanghui {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n,k;
        n = in.nextInt();
        k = in.nextInt();
        
        System.out.println(C(n,k));
        in.close();
    }
    public static int C(int n,int k){
        int[][] Y = new int[n + 1][n + 1];
        Y[0][0] = 1;
        for(int i = 0;i < n + 1;i++)
        {
            Y[i][0] = 1;
            Y[i][i] = 1;
        }
        for(int i = 2;i < n + 1;i++)
            for(int j = 1;j < i;j++)
                Y[i][j] = Y[i - 1][j - 1] + Y[i - 1][j];
        return Y[n][k];
    }
}

4.执行结果：

 

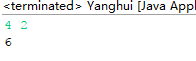
二、汉诺塔问题：

1.程序设计思想：

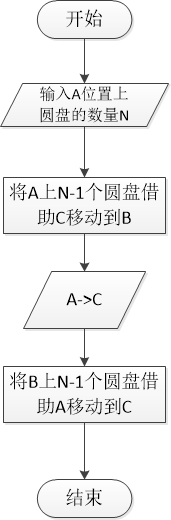
　　要将A位置上N个圆盘移动到C位置上，如果N = 1则直接移动，如果N > 1，则须

　　　　1）将A位置上N - 1个圆盘借助C移动到B位置

　　　　2）将A位置上剩下的一个圆盘移动到C位置

　　　　3）将B位置上N - 1个圆盘借助A移动到C位置

　　其中1）、3）可使用递归完成：

　　　　定义函数move(int n,char A,char B,char C)为：将A上n个圆盘借助B移动到C上（B、C为空），

　　　　则“1）”即递归调用move(n - 1,A,C,B)

　　　　　“2）”即递归调用move(n - 1,B,A,C)

2.程序流程图：

3.程序源代码：

import java.util.*;
public class Hanoi {
    public static void main(String[] args) {
        System.out.println("A位置上圆盘数量：");
        Scanner in = new Scanner(System.in);
        Hanoi(in.nextInt(),'A','B','C');
    }
    public static void Hanoi(int n,char a,char b,char c){
        if(n == 1)
            System.out.println(a + "->" + c);
        else{
            Hanoi(n - 1,a,c,b);
            System.out.println(a + "->" + c);
            Hanoi(n - 1,b,a,c);
        }
    }
}

4.执行结果：

三、判断回文字符串

1.程序设计思想：

2.程序流程图：

3.程序源代码：

import java.util.Scanner;

public class Palindrome {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        String str = in.next();
        System.out.println(isPalin(str));
    }
    
    public static boolean isPalin(String str){
        if(str.equals("") || str.length() == 1)
            return true;
        if(str.charAt(0) == str.charAt(str.length() - 1))
            return isPalin(str.substring(1, str.length() - 1));
        else return false;
    }
}

4.执行结果：