原文地址:你一定看得懂的关键路径概念 - 知乎 (zhihu.com)
在学习数据结构的过程中,我发现关键路径的中的概念取名使得第一印象让人容易产生误解,所以我用最通俗易懂的例子来解释解释这些概念的实际含义。
基本概念——AOE网
有几个最基本的概念我们要先了解,在带权有向图中,顶点表示事件,有向边表示活动,以边上的权值表示活动的开销,比如完成活动所需要的时间。这样的网络称为用边表示活动的网络,也就是AOE网。
分清发生和开始
这里要首先弄明白的是两个词,也就是后面要学到的概念中的 "发生" 和 "开始"。
“发生”是针对于事件的,也就是图中的顶点。什么叫事件发生了呢?
只有在指向该顶点的所有有向边对应的活动结束,该顶点所代表的事件才发生。
举个例子,一个事件C,它仅被两条边a, b指向,仅当a,b两活动都完成时,事件C发生。
“开始”是针对于活动的,也就是图中的边。
只有在一个顶点所代表的事件发生后,从该顶点出发的所有边对应的活动才能开始。
什么时候开始?即可以在事件一完成就立马开始接下来的活动,也可以推迟活动开始的时间。
最早发生时间——VE
到这里就已经能解释我们要说的第一个概念了,最早发生时间。
我猜这里应该经常会有人有疑惑,为什么是最长的路径长度决定最早的发生时间?我越想要早发生不是越应该走短的路径吗?
且听我说,摆脱困惑的重点是我们要和求最短路径的思路区分开,求最短路径是找尽可能短的路来保证路径长度最小,你只需要找出一条最短的路就行。但是在关键路径里,一个顶点是有多个前提的,只有前提的路径都走完,才能发生该顶点的事件,那么只有最长的路径走完,保证其余短的路都早已经走完,该事件才发生。
我们前面说过,发生是针对于事件的,一个事件要发生,首先要指向它的活动都完成。一个事件C,被两个活动a,b指向,a活动的耗费时间是3, b活动的耗费时间是5。那么看下图,从开始到C事件的发生要多久呢?
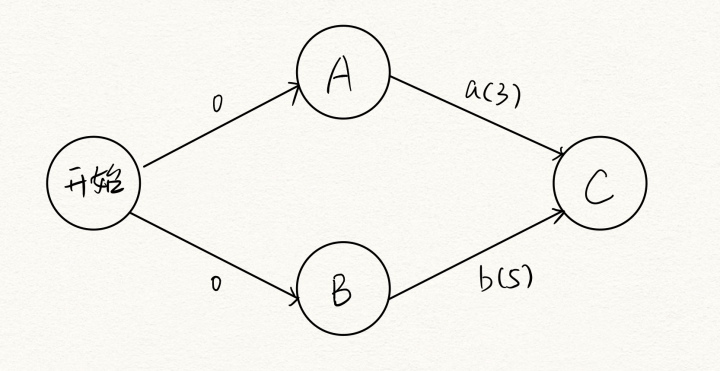
是最大路径长度5,因为C事件发生的前提必须是a,b两活动完成(活动可同时进行),C事件只有等到b完成才发生,最早完成时间由耗时最久的路决定,所以这就是为什么要取最长路径长度。
所以求目标顶点最早发生时间的方法是:
目标顶点的所有前提顶点(比如上图中C的前提顶点为A顶点和B顶点)的最早完成时间+对应的前提顶点到目标顶点的活动消耗 中的最大值。
比如C的最早完成时间是: Max{ A的最早完成时间+A到C的活动消耗时间, B的最早完成时间+B到C的活动消耗时间}
具体递推公式:
- ve(源点)=0
- ve(k) = Max{ ve{j} + Weight(j, k) }, j为k的任意前提顶点, Weight(j, k)表示<j, k>上的权值 。
只要从源点开始一直递推到汇点(终点)就好了。
最迟发生时间——VL
最迟发生时间的定义是这样的:在不推迟整个工程完成的前提下,保证后继事件j能在其最迟发生时间vl(j)能够发生时,该事件最迟必须发生的时间。
嚯!好家伙,自己的定义里套着自己,这一波套娃是真存心不想让人看懂。
首先,我们要知道,汇点的最迟发生时间就是它的最早发生时间(可以理解为汇点的最早发生时间就是工期),求VL的过程我们是从汇点倒着推回去的。
其次,为什么会有最迟发生时间呢?这是因为一个工程中,通常会存在某条路径耗时比其他路径久的多,所以耗时短的事件可以不必太早发生,也就是存在着缓冲时间。
为了方便理解,我举一个数据大小相差较大的例子:
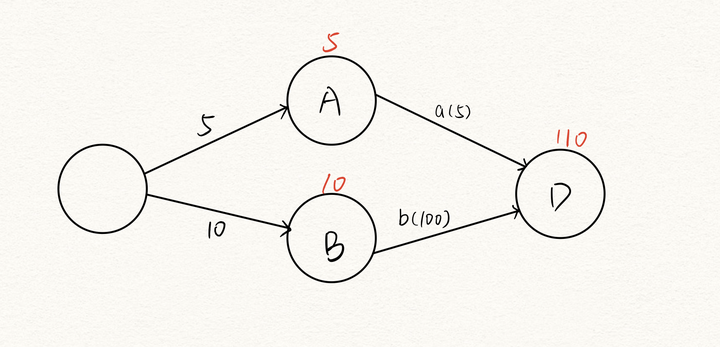
看看这个图,我在顶点上方写了它的最早发生时间,D是汇点,110是它的最早发生时间(也是最迟发生时间)。
此时我们可以这样理解,如果在110天时工程必须完成,那么A事件最迟什么时候要发生?
我们可以用110减去a活动用时,得到105,也就是说A事件最迟可以在第105天发生(一旦发生就要立刻开始a活动,否则将推迟整个工期),指向A的活动可以在第100天才开始。
而A事件最早可以在第5天就发生(这里说最早才有意义了),最早第5天完成,但是可以推迟到第105天完成,中间差了100天了。
同理可得B事件的最迟发生时间是第10天,它一刻也不能拖。
这时候再回去看看最迟发生时间的定义,应该就可以理解了吧
再刚刚举的例子里,AB事件是相互独立的,如果我再添加一个不独立的事件:
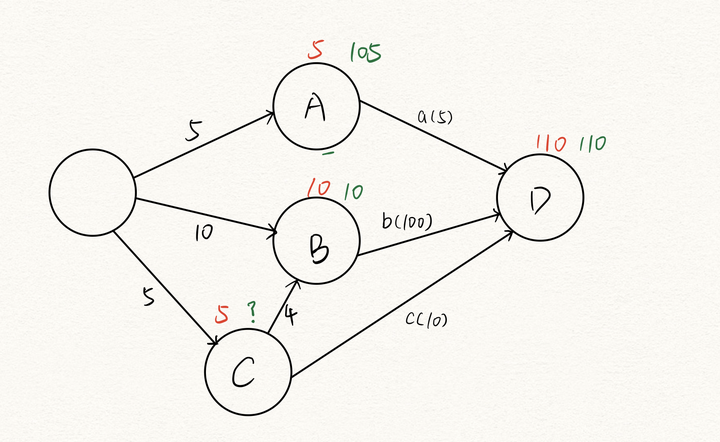
这个图中我添加了一个C顶点,它是B顶点的前提。我把已知的最迟发生时间用绿色笔迹写在了最早发生时间右边。一起看看C事件的最迟发生时间是多少吧。
这里我们可以看到,和上图不同,C顶点有2个出度,也就意味着它影响着两个后继顶点。
如果我们仍用上次的方法,用110-10得100,可以认为C事件最迟在第100天发生吗?
仔细看看是不对的,B顶点的发生前提是C顶点要发生,如果C在第100天才发生,那么B事件等不了啊,B最迟在第10天就要发生,等到第100天干脆毁灭吧
正确的做法应该是B事件的最迟发生时间减4天得第6天。由此可见,一个顶点的最迟发生时间其实是由它的后继节点所决定的,这也就解答了为什么我们要从汇点开始倒着往起点推。
我想你也可以理解了为什么公式中使用的是 Min{} 取最小。就比如刚刚的例子,C有两个选择——第6天或者第100天,你必须得选最小的以保证你不会耽误任何后继节点的最迟发生。
递推公式:
vl(汇点) = ve(汇点)
vl(k) = Min{ vl(j) - Weight(k, j) } ,k为j的任意前驱
活动的最早开始时间——e和最迟开始时间——l
这两个概念相比之前的就简单多了,首先,还记得我在一开始说的吗,“开始”是针对活动,也就是图中的边的概念。
活动的最早开始时间,理解起来非常容易,边的起点事件一旦发生就立刻开始,就是最早开始时间了。
公式:若边<k, j> 表示活动i,则有e(i) = ve(k)
那最迟开始时间呢,这要和该边指向事件的最迟发生时间挂钩,假如在10点必须写完作业(事件),写作业(活动)要2小时,那最晚啥时候开始写作业呢?8点对吧,也就是边所指向的事件最晚发生时间 - 边对应的活动所需时间。
公式: 若边<k, j> 表示活动i,则有l(i) = vl(j) - Weight(k,j)
时间余量d
d(i) = l(i) - e(i),即活动最迟开始时间与最早开始时间的差额,这代表着活动可以拖延的时间。如果一个活动的时间余量为0,就意味着该活动不能拖延时间,称为关键活动,必须立即完成,否则就将拖延整个工期。
而时间余量为0的所有边连起来,就是关键路径了。
要求时间余量d, 就要先求活动的最早开始时间e和最迟开始时间l,要求e和l就要先求事件最早发生时间ve和最迟发生时间vl。所以做题步骤就出来啦,最后来做一题试试看吧!
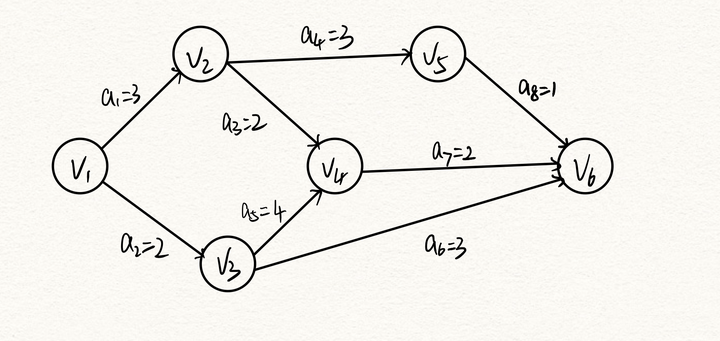
答案:


最终得到的关键路径为(v1, v3, v4, v6)
最后注意的几点:
- 关键路径上的所有活动都是关键活动, 它是决定整个工程的关键因素,因此可以通过加快关键活动来缩短整个工期。但是也不能任意缩短,因为一旦缩短到一定的程度,该关键活动就可能变成非关键活动了
- 网中的关键路径不唯一,对于有好几条关键路径的网,只加快其中某一条关键路径上的活动并不能缩短工期。只有加快存在于所有关键路径上的关键活动才能达到缩短工期的目的。