理解：语法树，短语，直接短语，句柄

概念：

语法树求短语、简单短语和句柄：

1）短语：子树的末端结点形成的符号串。

2）简单子树：只有一层分支的子树。

3）直接短语（简单短语）：简单子树的末端结点形成的符号串。

4）句柄：子树中最左边的那棵只有父子两代的子树的所有叶结点自左至右排列起来，就是该句型的句柄。

 例子：

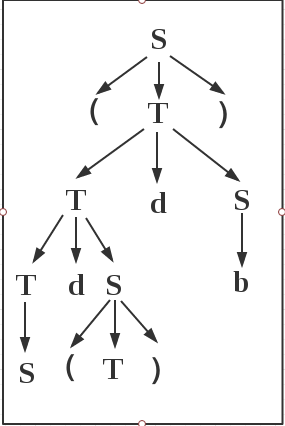
由此可得S=(Sd(T)db)为此文法的一个句型：

• 短语:S，(T)，b，Sd(T)，Sd(T)db，（Sd(T)db)

• 直接短语:S，(T)，b

• 句柄:S

• 此时的最左直接短语是S所有句柄为S

题目：

1.已知文法：

S->a|^|(T)

T->T,S|S

分析句型（T,(^,a))，求全部的短语、直接短语和句柄。

 　　答：依题意得到语法树如下图：

　　　　全部短语：(T,(^,a))　　T,(^,a)　　(^,a)　　^,a　　^　　a

　　　　直接短语：^　　a

　　　　句柄：^

2.构造上下文无关文法，描述语言：

 （1）｛aⁿbⁿ|n>=0｝

 （2）｛a^mbⁿ|m>=n>=0｝

 （3）   if语句

 （4）｛(ab)ⁿ|n>=0｝

 （5）｛a^mbⁿ|m,n>=1｝

　　答：（1）G[S]：S -> aSb | ab | ε

　　　　　　由S产生任意多个相同数量的a和b

　　　　（2）G[S]：S -> aSb | a | ε

　　　　　　由S产生任意多个a和任意多个b，数量a比b多

　　　　（3）if语句 -> if<条件>then<语句> | if<条件>then<语句>else<语句>

　　　　（4）G[S]：S -> aSb | aaSbb | ... | (ab)ⁿ | ε

　　　　　　由S产生任意多个相同数量的a和b

　　　　（5）G[S]：S -> aS|Sb | a | ε

　　　　　　由S产生任意多个a和任意多个b，a和b的个数都大于1个

3.如果if语句的方法：

stmt->if expr then stmt

     | if expr then stmt else stmt

     | other

句子if E1 then if E2 then S1 else S2是否有两棵不同的语法树？说明了什么？

　　答：依题意画出语法树如下图：

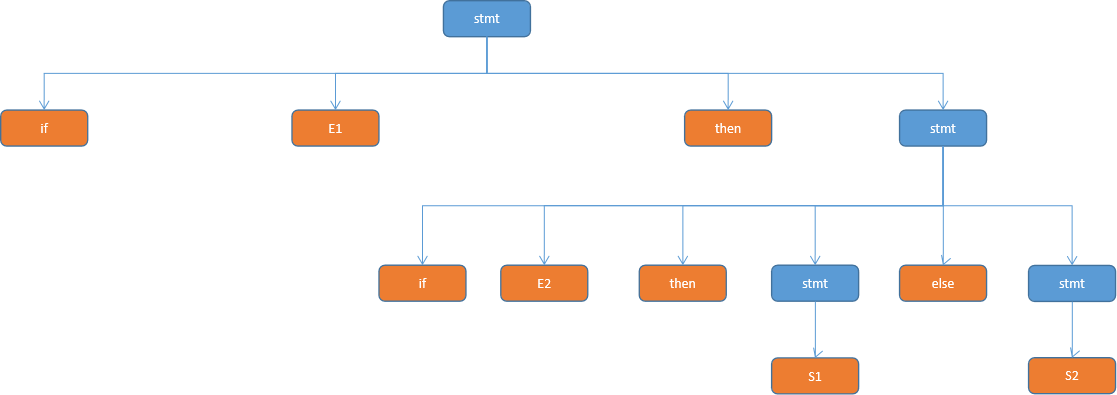
语法树（1）

 

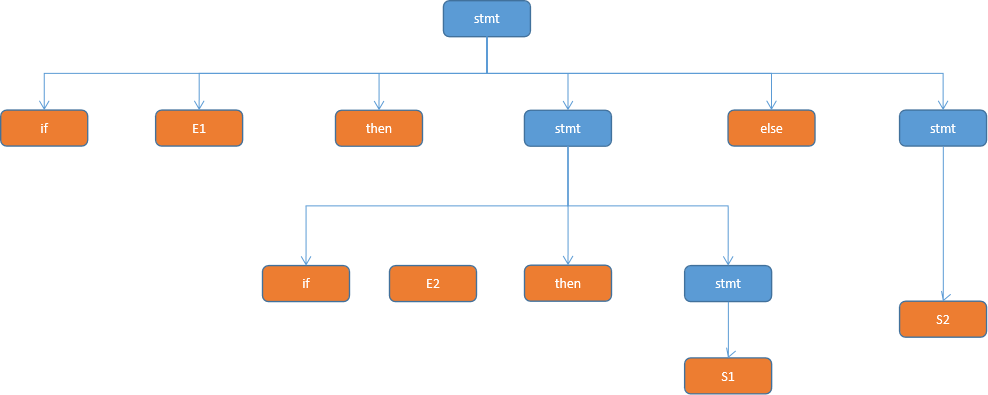
语法树（2）

　　依题意可以画出两颗语法树，两颗语法树都是可以描述同一个文法的。这说明了这个文法是二义性的。