codeforces 922F Divisibility 构造

F. Divisibility

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Imp is really pleased that you helped him. But it you solve the last problem, his gladness would raise even more.

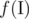Let's define  for some set of integers  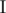as the number of pairs a, b in 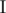, such that:

• a is strictly less than b;
• a divides b without a remainder.

You are to find such a set 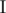, which is a subset of {1, 2, ..., n} (the set that contains all positive integers not greater than n), that .

Input

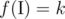The only line contains two integers n and k .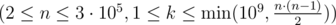

Output

If there is no answer, print "No".

Otherwise, in the first line print "Yes", in the second — an integer m that denotes the size of the set 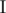 you have found, in the second line print m integers — the elements of the set 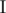, in any order.

If there are multiple answers, print any of them.

Examples

input

3 3

output

No

input

6 6

output

Yes
5
1 2 4 5 6 

input

8 3

output

Yes
4
2 4 5 8

Note

In the second sample, the valid pairs in the output set are (1, 2), (1, 4), (1, 5), (1, 6), (2, 4), (2, 6). Thus, .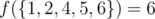

In the third example, the valid pairs in the output set are (2, 4), (4, 8), (2, 8). Thus,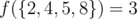 

题意：I 是一个正整数集合，I中取两个数a,b( a > b )使得a%b==0 的(a,b)组数定义为 f(I)

给定N，K，问是否存在f(I)=K，并且 I 中的元素小于等于N的 集合 I  ，若有，输出任意方案

题解：构造，cf的独特题目类型，变化太多了。直接说（抄来的）题解吧：

第一步：

先让 I 包含从1到m的所有数，使此时的 f(I) 恰好大于等于K

(恰好的含义是 ：若 I 包含从1到m-1的所有数，f(i)<K)

找到这样的m。

如何找？可以用筛法求出 b 与比它小的数组成的合法数对个数，记为val[b]，然后求val的累加和，找到临界点，就能找到m。

第二步：

考虑从当前 集合 中删除一些数。

只考虑删除素数（删除合数计算贡献太麻烦）

素数b对当前答案的贡献是m/b。

越大的素数对当前答案的贡献越小，所以可以考虑从小到大删除素数，维护当前答案。

至于为什么删除素数就可以……不会证明。

细节可以见代码

/*
Welcome Hacking
Wish You High Rating
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
using namespace std;
int read(){
    int xx=0,ff=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')ff=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){xx=xx*10+ch-'0';ch=getchar();}
    return xx*ff;
}
const int maxn=300005;
int N,K,val[maxn],prime[30000],cnt,limit,ans;
bool del[maxn];
void pre(){
    for(int i=2;i<=N;i++){
        if(!val[i])
            prime[++cnt]=i;
        val[i]++;
        for(int j=i+i;j<=N;j+=i)
            val[j]++;
    }
}
int main(){
    //freopen("in","r",stdin);
    N=read(),K=read();
    pre();
    long long tot=0;
    for(int i=1;i<=N;i++){
        tot+=val[i];
        if(tot>=K){
            ans=limit=i;
            break;
        }
    }
    if(tot>K)
        for(int i=1;i<=cnt;i++){
            if(tot==K)
                break;
            if(tot-K>=limit/prime[i]){
                del[prime[i]]=1;
                tot-=limit/prime[i];
                ans--;
            }
        }
    if(tot!=K)
        printf("No
");
    else{
        printf("Yes
");
        printf("%d
",ans);
        for(int i=1;i<=limit;i++)
            if(!del[i])
                printf("%d ",i);
        puts("");
    }
    return 0;
}