[LeetCode] 694. Number of Distinct Islands

Given a non-empty 2D array grid of 0's and 1's, an island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

Count the number of distinct islands. An island is considered to be the same as another if and only if one island can be translated (and not rotated or reflected) to equal the other.

Example 1:

11000
11000
00011
00011

Given the above grid map, return 1.

 

Example 2:

11011
10000
00001
11011

Given the above grid map, return 3.

Notice that:

11
1

and

 1
11

are considered different island shapes, because we do not consider reflection / rotation.

 

Note: The length of each dimension in the given grid does not exceed 50.

Algorithm:

We can use BFS or DFS to count the number of islands, then remove duplicated counts of the same shape islands.  The search part is fairly straightforward, the hard part is how to track the different shapes of islands we've encountered so far.

We'll use BFS and fix the neighboring cells search order to be up, right, down then left. And we perform BFS for unvisited cells of value 1 from the 1st row to last, from the 1st column to last for each row. This way gurantees that for the same shape of islands, each cell is visited in matching orders. The only difference at this point is the actuall cell positions. Since for the same shape islands, they have the same internal relative cell positions, we can simply do the following for normalization purpose.

For each new island, make its first visited cell as position(0, 0) and adjust the other cells' positions of this island accordingly. This way, the same shape islands have the exactly the same list of cell positions.

There are 2 different ways of tracking each island's cell list.

1. Built in Java List hashing/equality check

Java 8 has a nice List interface that already overwrites hashCode() and equals() for List comparison. As a result we can either store each cell position as a list of size 2 or define a Cell class that overwrites hashCode() and equals(), then store the list of an island's cells in a HashSet. Storing cell position as int[] does not work, because the default hashcode of int[] is its memory address, this means each time a new int[] is created, even if they have the same values inside, they are still treated as not equal.

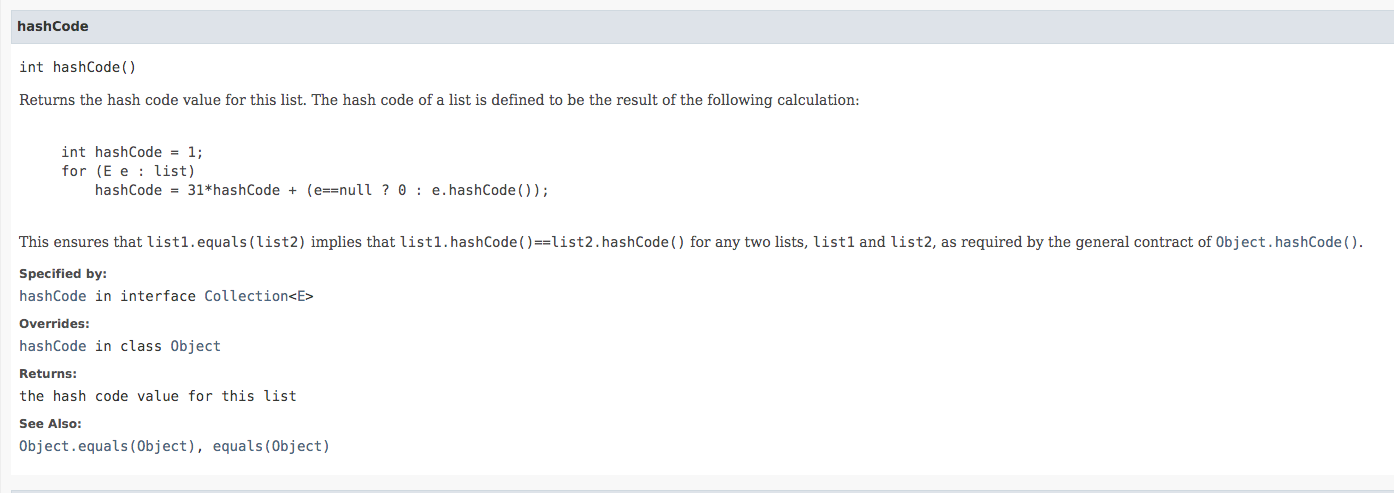
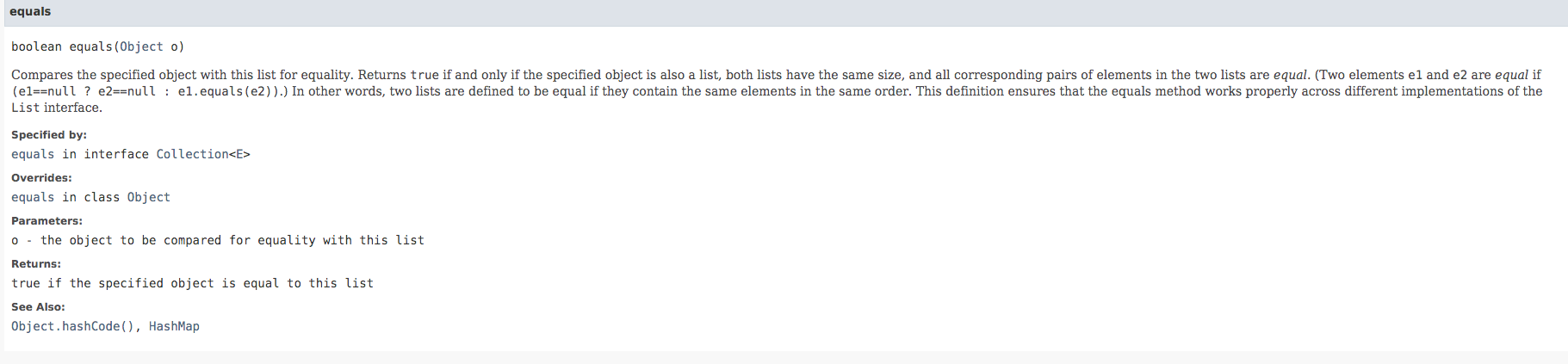
Solution 1. BFS + built-in Java List hashing + HashSet. 

Using list of size 2.

class Solution {
    private int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
    public int numDistinctIslands(int[][] grid) {
        Set<List<List<Integer>>> unique = new HashSet<>();
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(!visited[i][j] && grid[i][j] == 1) {
                    unique.add(bfs(grid, visited, i, j));
                }
            }
        }
        return unique.size();
    }
    private List<List<Integer>> bfs(int[][] grid, boolean[][] visited, int x, int y) {
        List<List<Integer>> island = new ArrayList<>();
        Queue<int[]> q = new LinkedList<>();
        Queue<int[]> offset = new LinkedList<>();
        q.add(new int[]{x, y});
        offset.add(new int[]{0,0});
        visited[x][y] = true;
        
        while(q.size() > 0) {
            int[] curr = q.poll();
            int[] currOffset = offset.poll();
            List<Integer> list = new ArrayList<>();
            list.add(currOffset[0]); list.add(currOffset[1]); 
            island.add(list);
            for(int dir = 0; dir < 4; dir++) {
                int x1 = curr[0] + dx[dir];
                int y1 = curr[1] + dy[dir];
                int offsetX = currOffset[0] + dx[dir];
                int offsetY = currOffset[1] + dy[dir];
                if(inBound(grid, x1, y1) && !visited[x1][y1] && grid[x1][y1] == 1) {
                    q.add(new int[]{x1, y1});
                    offset.add(new int[]{offsetX, offsetY});
                    visited[x1][y1] = true;
                }
            }
        }
        return island; 
    }
    private boolean inBound(int[][] grid, int x, int y) {
        return x >= 0 && x < grid.length && y >= 0 && y < grid[0].length;
    }
}

Using Helper class definition

class Solution {
    class Cell {
        private int[] pos;
        Cell(int[] pos) {
            this.pos = pos;
        }
        @Override
        public int hashCode() {
            return Arrays.hashCode(pos);
        }
        @Override
        public boolean equals(Object o) {
            if (this == o) return true;
            if (o == null || getClass() != o.getClass()) return false;
            Cell other = (Cell) o;
            return Arrays.equals(pos, other.pos);
        }
    }
    private int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
    public int numDistinctIslands(int[][] grid) {
        Set<List<Cell>> unique = new HashSet<>();
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(!visited[i][j] && grid[i][j] == 1) {
                    unique.add(bfs(grid, visited, i, j));
                }
            }
        }
        return unique.size();
    }
    private List<Cell> bfs(int[][] grid, boolean[][] visited, int x, int y) {
        List<Cell> island = new ArrayList<>();
        Queue<int[]> q = new LinkedList<>();
        Queue<int[]> offset = new LinkedList<>();
        q.add(new int[]{x, y});
        offset.add(new int[]{0,0});
        visited[x][y] = true;
        
        while(q.size() > 0) {
            int[] curr = q.poll();
            int[] currOffset = offset.poll();
            island.add(new Cell(currOffset));
            for(int dir = 0; dir < 4; dir++) {
                int x1 = curr[0] + dx[dir];
                int y1 = curr[1] + dy[dir];
                int offsetX = currOffset[0] + dx[dir];
                int offsetY = currOffset[1] + dy[dir];
                if(inBound(grid, x1, y1) && !visited[x1][y1] && grid[x1][y1] == 1) {
                    q.add(new int[]{x1, y1});
                    offset.add(new int[]{offsetX, offsetY});
                    visited[x1][y1] = true;
                }
            }
        }
        return island; 
    }
    private boolean inBound(int[][] grid, int x, int y) {
        return x >= 0 && x < grid.length && y >= 0 && y < grid[0].length;
    }
}

Solution 2. BFS + TreeSet + Customized Comparator. 

TreeSet's implementation is not hashing based(Red Black Tree based), so we can store List of int[] in a TreeSet with a customized comparator.

class Solution {
    private int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};
    public int numDistinctIslands(int[][] grid) {
        TreeSet<List<int[]>> unique = new TreeSet<>((l1, l2) -> {
            if(l1.size() != l2.size()) {
                return l1.size() - l2.size();
            }
            for(int i = 0; i < l1.size(); i++) {
                if(l1.get(i)[0] < l2.get(i)[0]) {
                    return -1;
                }
                else if(l1.get(i)[0] > l2.get(i)[0]) {
                    return 1;
                }
                else if(l1.get(i)[1] < l2.get(i)[1]) {
                    return -1;
                }
                else if(l1.get(i)[1] > l2.get(i)[1]) {
                    return 1;
                }
            }
            return 0;
        });
        boolean[][] visited = new boolean[grid.length][grid[0].length];
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(!visited[i][j] && grid[i][j] == 1) {
                    unique.add(bfs(grid, visited, i, j));
                }
            }
        }
        return unique.size();
    }
    private List<int[]> bfs(int[][] grid, boolean[][] visited, int x, int y) {
        List<int[]> island = new ArrayList<>();
        Queue<int[]> q = new LinkedList<>();
        Queue<int[]> offset = new LinkedList<>();
        q.add(new int[]{x, y});
        offset.add(new int[]{0,0});
        visited[x][y] = true;
        
        while(q.size() > 0) {
            int[] curr = q.poll();
            int[] currOffset = offset.poll();
            island.add(currOffset);
            for(int dir = 0; dir < 4; dir++) {
                int x1 = curr[0] + dx[dir];
                int y1 = curr[1] + dy[dir];
                int offsetX = currOffset[0] + dx[dir];
                int offsetY = currOffset[1] + dy[dir];
                if(inBound(grid, x1, y1) && !visited[x1][y1] && grid[x1][y1] == 1) {
                    q.add(new int[]{x1, y1});
                    offset.add(new int[]{offsetX, offsetY});
                    visited[x1][y1] = true;
                }
            }
        }
        return island; 
    }
    private boolean inBound(int[][] grid, int x, int y) {
        return x >= 0 && x < grid.length && y >= 0 && y < grid[0].length;
    }
}

Reference:

Working with hashcode and equals in Java