Given a binary tree, return the vertical order traversal of its nodes values.
For each node at position (X, Y), its left and right children respectively will be at positions (X-1, Y-1) and (X+1, Y-1).
Running a vertical line from X = -infinity to X = +infinity, whenever the vertical line touches some nodes, we report the values of the nodes in order from top to bottom (decreasing Y coordinates).
If two nodes have the same position, then the value of the node that is reported first is the value that is smaller.
Return an list of non-empty reports in order of X coordinate. Every report will have a list of values of nodes.
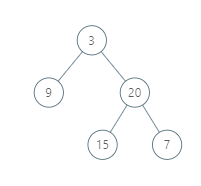
Example 1:
Input: [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Explanation:
Without loss of generality, we can assume the root node is at position (0, 0):
Then, the node with value 9 occurs at position (-1, -1);
The nodes with values 3 and 15 occur at positions (0, 0) and (0, -2);
The node with value 20 occurs at position (1, -1);
The node with value 7 occurs at position (2, -2).
Example 2:
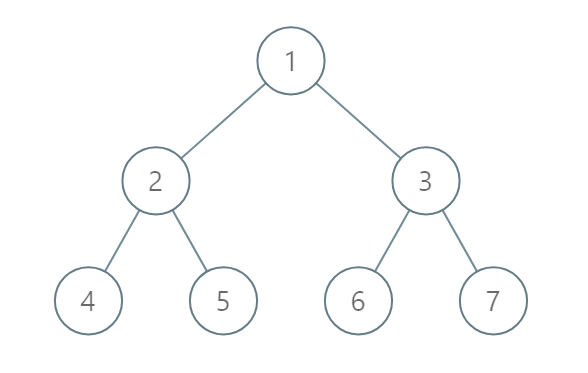
Input: [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
The node with value 5 and the node with value 6 have the same position according to the given scheme.
However, in the report "[1,5,6]", the node value of 5 comes first since 5 is smaller than 6.
Note:
- The tree will have between 1 and
1000nodes. - Each node's value will be between
0and1000.
Solution 1. O(N * logN) by implementing a location class that is sortable based on x, y, and its value.
1 class Solution { 2 class Location implements Comparable<Location>{ 3 int x, y, val; 4 Location(int x, int y, int val) { 5 this.x = x; 6 this.y = y; 7 this.val = val; 8 } 9 10 @Override 11 public int compareTo(Location that) { 12 if (this.x != that.x) 13 return Integer.compare(this.x, that.x); 14 else if (this.y != that.y) 15 return Integer.compare(this.y, that.y); 16 else 17 return Integer.compare(this.val, that.val); 18 } 19 } 20 private List<Location> locations; 21 public List<List<Integer>> verticalTraversal(TreeNode root) { 22 // Each location is a node's x position, y position, and value 23 locations = new ArrayList(); 24 dfs(root, 0, 0); 25 Collections.sort(locations); 26 27 List<List<Integer>> ans = new ArrayList(); 28 ans.add(new ArrayList<Integer>()); 29 30 int prev = locations.get(0).x; 31 32 for (Location loc: locations) { 33 // If the x value changed, it's part of a new report. 34 if (loc.x != prev) { 35 prev = loc.x; 36 ans.add(new ArrayList<Integer>()); 37 } 38 39 // We always add the node's value to the latest report. 40 ans.get(ans.size() - 1).add(loc.val); 41 } 42 43 return ans; 44 } 45 46 public void dfs(TreeNode node, int x, int y) { 47 if (node != null) { 48 locations.add(new Location(x, y, node.val)); 49 dfs(node.left, x-1, y+1); 50 dfs(node.right, x+1, y+1); 51 } 52 } 53 }
We can also implement a Comparator interface to achieve the same sorting goal.
1 class Solution { 2 class Location { 3 int x, y, val; 4 Location(int x, int y, int val) { 5 this.x = x; 6 this.y = y; 7 this.val = val; 8 } 9 } 10 private List<Location> locations; 11 public List<List<Integer>> verticalTraversal(TreeNode root) { 12 // Each location is a node's x position, y position, and value 13 locations = new ArrayList(); 14 dfs(root, 0, 0); 15 Collections.sort(locations, new Comparator<Location>() { 16 @Override 17 public int compare(Location l1, Location l2) { 18 int xDiff = l1.x - l2.x; 19 if(xDiff != 0) { 20 return xDiff; 21 } 22 int yDiff = l1.y - l2.y; 23 if(yDiff != 0) { 24 return yDiff; 25 } 26 return l1.val - l2.val; 27 } 28 }); 29 30 List<List<Integer>> ans = new ArrayList(); 31 ans.add(new ArrayList<Integer>()); 32 33 int prev = locations.get(0).x; 34 35 for (Location loc: locations) { 36 // If the x value changed, it's part of a new report. 37 if (loc.x != prev) { 38 prev = loc.x; 39 ans.add(new ArrayList<Integer>()); 40 } 41 42 // We always add the node's value to the latest report. 43 ans.get(ans.size() - 1).add(loc.val); 44 } 45 46 return ans; 47 } 48 49 public void dfs(TreeNode node, int x, int y) { 50 if (node != null) { 51 locations.add(new Location(x, y, node.val)); 52 dfs(node.left, x-1, y+1); 53 dfs(node.right, x+1, y+1); 54 } 55 } 56 }
Solution 2. Use treemap of treemap to keep nodes sorted first by x, then by y.
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode(int x) { val = x; } 8 * } 9 */ 10 class Solution { 11 public List<List<Integer>> verticalTraversal(TreeNode root) { 12 TreeMap<Integer, TreeMap<Integer, List<Integer>>> map = new TreeMap<>(); 13 traverse(root, 0, 0, map); 14 List<List<Integer>> result = new ArrayList<>(); 15 while(map.size() > 0) { 16 TreeMap<Integer, List<Integer>> sameX = map.pollFirstEntry().getValue(); 17 List<Integer> list = new ArrayList<>(); 18 while(sameX.size() > 0) { 19 List<Integer> sameY = sameX.pollLastEntry().getValue(); 20 Collections.sort(sameY); 21 list.addAll(sameY); 22 } 23 result.add(list); 24 } 25 return result; 26 } 27 private void traverse(TreeNode node, int x, int y, TreeMap<Integer, TreeMap<Integer, List<Integer>>> map) { 28 if(node == null) { 29 return; 30 } 31 if(!map.containsKey(x)) { 32 map.put(x, new TreeMap<>()); 33 } 34 if(!map.get(x).containsKey(y)) { 35 map.get(x).put(y, new ArrayList<>()); 36 } 37 map.get(x).get(y).add(node.val); 38 traverse(node.left, x - 1, y - 1, map); 39 traverse(node.right, x + 1, y - 1, map); 40 } 41 }
This problem is similar with Binary Tree Vertical Order Traversal on LintCode. The only difference is how to handle nodes that are in the same position. This one uses natural ordering to break ties, whereas the lintcode problem uses left to right ordering.