Ilya is sitting in a waiting area of Metropolis airport and is bored of looking at time table that shows again and again that his plane is delayed. So he took out a sheet of paper and decided to solve some problems.
First Ilya has drawn a grid of size n × n and marked n squares on it, such that no two marked squares share the same row or the same column. He calls a rectangle on a grid with sides parallel to grid sides beautiful if exactly two of its corner squares are marked. There are exactly n·(n - 1) / 2 beautiful rectangles.
Ilya has chosen q query rectangles on a grid with sides parallel to grid sides (not necessarily beautiful ones), and for each of those rectangles he wants to find its beauty degree. Beauty degree of a rectangle is the number of beautiful rectangles that share at least one square with the given one.
Now Ilya thinks that he might not have enough time to solve the problem till the departure of his flight. You are given the description of marked cells and the query rectangles, help Ilya find the beauty degree of each of the query rectangles.
The first line of input contains two integers n and q (2 ≤ n ≤ 200 000, 1 ≤ q ≤ 200 000) — the size of the grid and the number of query rectangles.
The second line contains n integers p1, p2, ..., pn, separated by spaces (1 ≤ pi ≤ n, all pi are different), they specify grid squares marked by Ilya: in column i he has marked a square at row pi, rows are numbered from 1 to n, bottom to top, columns are numbered from 1 to n, left to right.
The following q lines describe query rectangles. Each rectangle is described by four integers: l, d, r, u (1 ≤ l ≤ r ≤ n, 1 ≤ d ≤ u ≤ n), here land r are the leftmost and the rightmost columns of the rectangle, d and u the bottommost and the topmost rows of the rectangle.
For each query rectangle output its beauty degree on a separate line.
2 3
1 2
1 1 1 1
1 1 1 2
1 1 2 2
1
1
1
4 2
1 3 2 4
4 1 4 4
1 1 2 3
3
5
The first sample test has one beautiful rectangle that occupies the whole grid, therefore the answer to any query is 1.
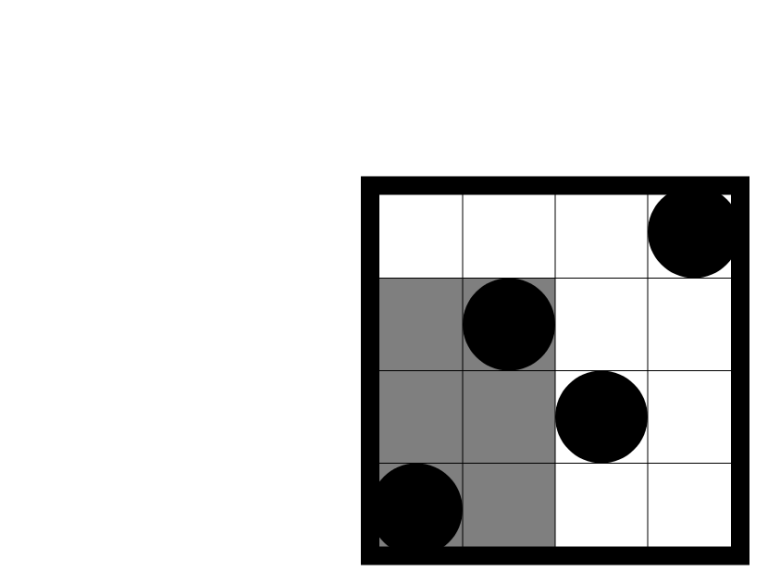
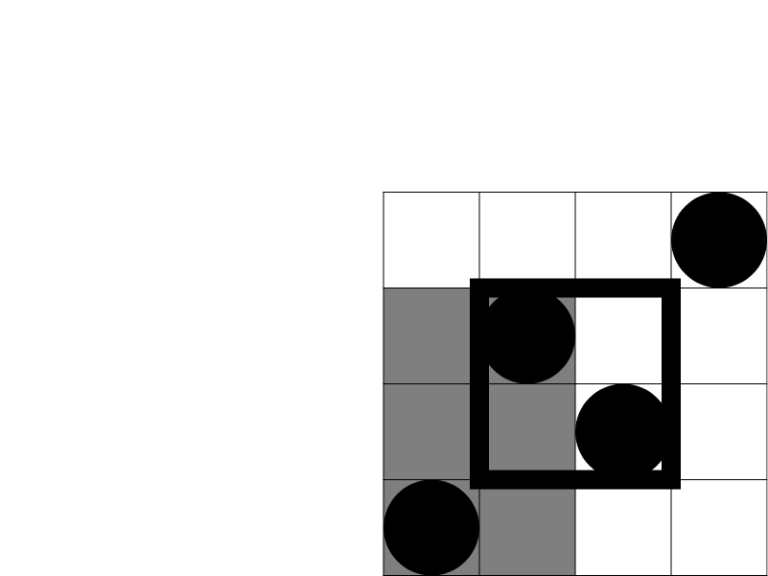
In the second sample test the first query rectangle intersects 3 beautiful rectangles, as shown on the picture below:

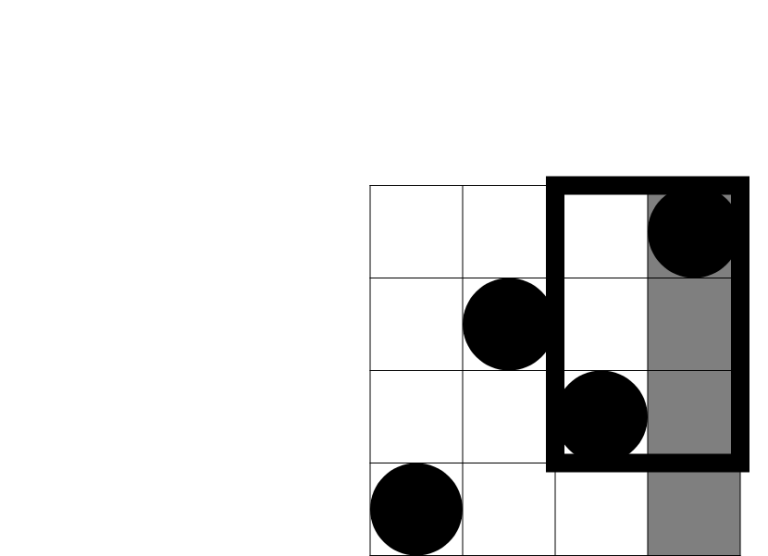
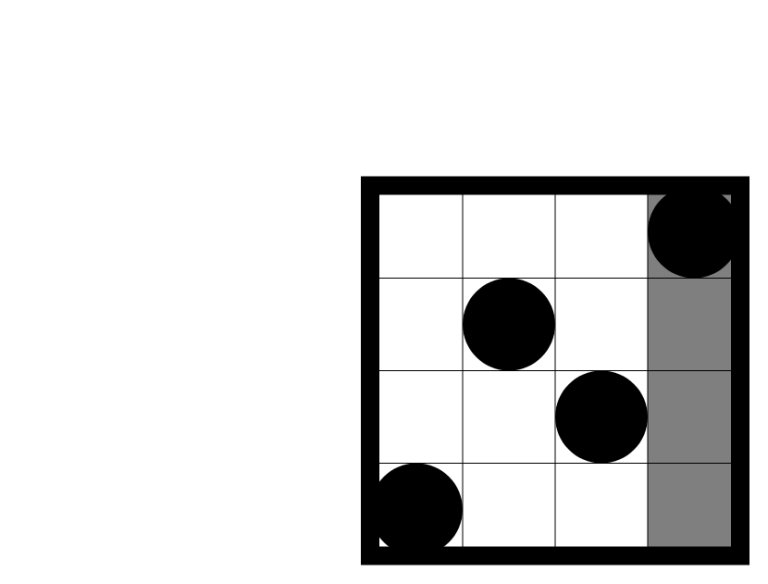
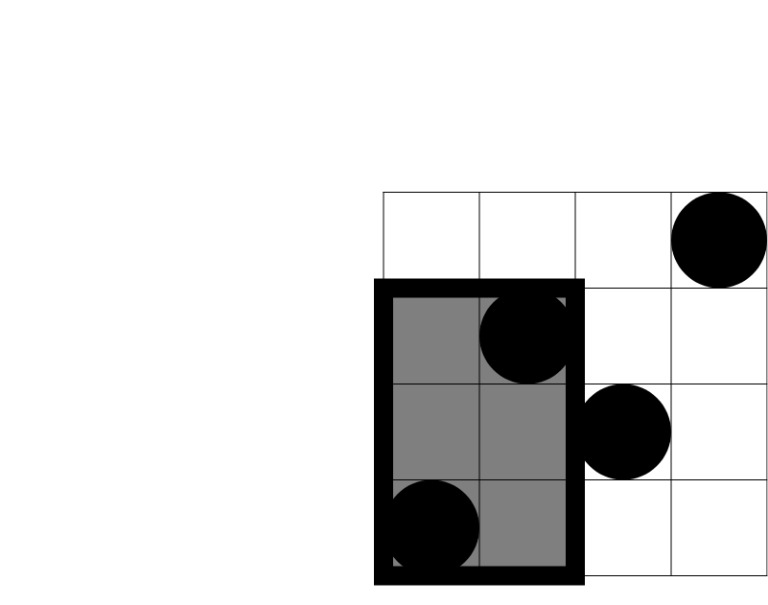
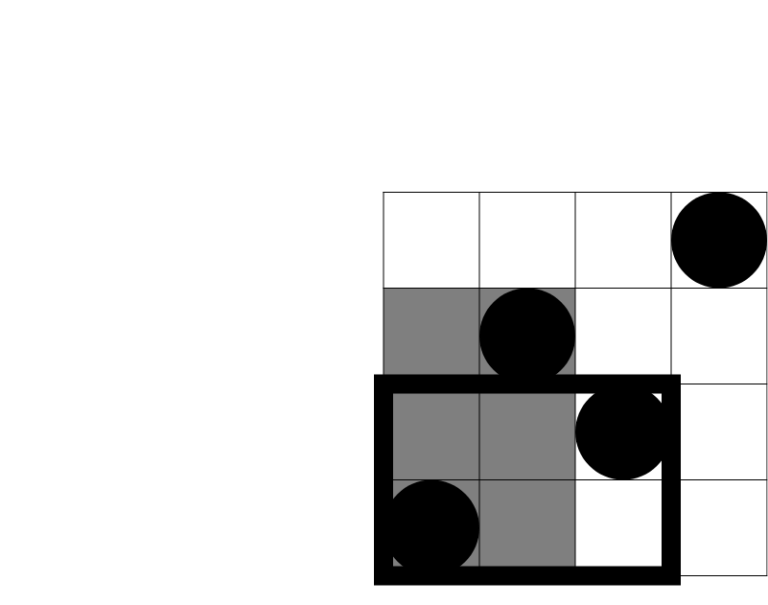
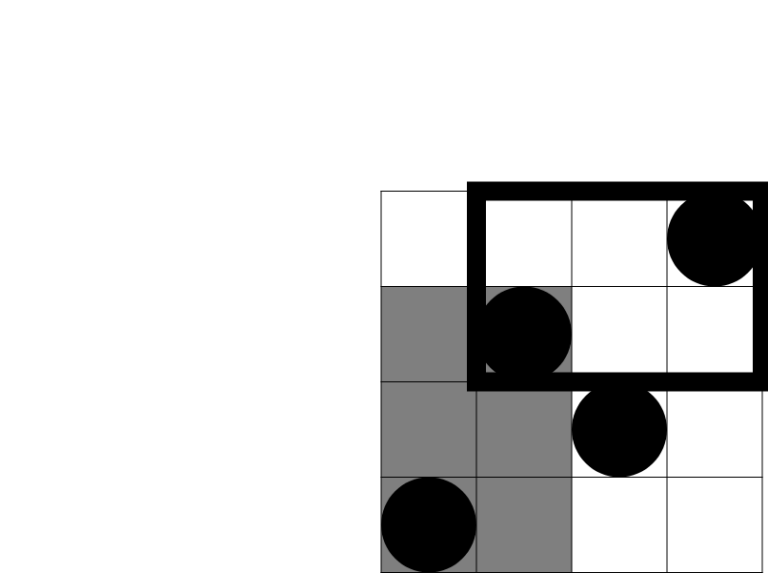
There are 5 beautiful rectangles that intersect the second query rectangle, as shown on the following picture:
这道题 题意就是给你n个点 这n个点 两两可以组成一个矩阵(作为两个角的位置)
然后给你q个询问 询问给你一个矩阵的左上角和右上角 求 n个点两两配对组成的矩阵有多少个和他有交
这道题我的写法可能有点暴力
就是把一个矩阵的四条边延长 延长之后呢 就变成了九个矩阵
这样就变成了这九个矩阵之间两两配对之后是否和矩阵有交
这个画一下图应该就可以了 至于求每个矩阵中有多少个点
就可以利用扫描线来实现 一个询问拆成9个 容斥一下就可以得到全部答案了
复杂度主要是排序的nlogn 当然因为拆询问的缘故 n要乘9
代码略丑QAQ

#include<cstdio> #include<cstring> #include<algorithm> #define LL long long using namespace std; const int M=2e6+7; int read(){ int ans=0,f=1,c=getchar(); while(c<'0'||c>'9'){if(c=='-') f=-1; c=getchar();} while(c>='0'&&c<='9'){ans=ans*10+(c-'0'); c=getchar();} return ans*f; } LL tot; int s[3*M]; LL ans[M][10]; int n,m,xp,qp,ep; int lowbit(int x){return x&-x;} void add(int x,LL v){ while(x<=n){ s[x]+=v; x+=lowbit(x); } } int query(int x){ LL ans=0; while(x){ ans+=s[x]; x-=lowbit(x); } return ans; } struct Q{ int r,h,id,pos; bool operator <(const Q& x)const{return h<x.h;} void calc(){ans[id][pos]=query(r);} }q[2*M]; struct pos{ int x,y,w; bool operator <(const pos& h)const{return y<h.y;} void calc(){add(x,w);} }e[M]; int main() { int x1,y1,x2,y2; n=read(); m=read(); for(int i=1;i<=n;i++){ y1=read(); e[ep++]=(pos){i,y1,1}; } for(int i=1;i<=m;i++){ x1=read(); y1=read(); x2=read(); y2=read(); q[qp++]=(Q){x1-1,y1-1,i,1}; q[qp++]=(Q){x1-1,y2,i,2}; q[qp++]=(Q){x1-1,n,i,3}; q[qp++]=(Q){x2,y1-1,i,4}; q[qp++]=(Q){x2,y2,i,5}; q[qp++]=(Q){x2,n,i,6}; q[qp++]=(Q){n,y1-1,i,7}; q[qp++]=(Q){n,y2,i,8}; q[qp++]=(Q){n,n,i,9}; } sort(e,e+ep); sort(q,q+qp); for(int i=0,j=0;i<qp;i++){ while(j<ep&&e[j].y<=q[i].h) e[j++].calc(); q[i].calc(); } for(int i=1;i<=m;i++){ tot=0; LL h[10]; h[1]=ans[i][1]; h[2]=ans[i][2]-ans[i][1]; h[3]=ans[i][3]-ans[i][2]; h[4]=ans[i][4]-ans[i][1]; h[5]=ans[i][5]-ans[i][4]-ans[i][2]+ans[i][1]; h[6]=ans[i][6]-ans[i][5]-ans[i][3]+ans[i][2]; h[7]=ans[i][7]-ans[i][4]; h[8]=ans[i][8]-ans[i][7]-ans[i][5]+ans[i][4]; h[9]=ans[i][9]-ans[i][8]-ans[i][6]+ans[i][5]; tot=tot+h[5]*(h[1]+h[2]+h[3]+h[4]+h[6]+h[7]+h[8]+h[9]); tot=tot+h[5]*(h[5]-1)/2; tot=tot+h[4]*(h[8]+h[9]+h[6]); tot=tot+h[6]*(h[7]+h[8]); tot=tot+h[1]*(h[6]+h[8]+h[9]); tot=tot+h[3]*(h[4]+h[7]+h[8]); tot=tot+h[2]*(h[4]+h[6]+h[7]+h[8]+h[9]); printf("%I64d ",tot); } return 0; }
